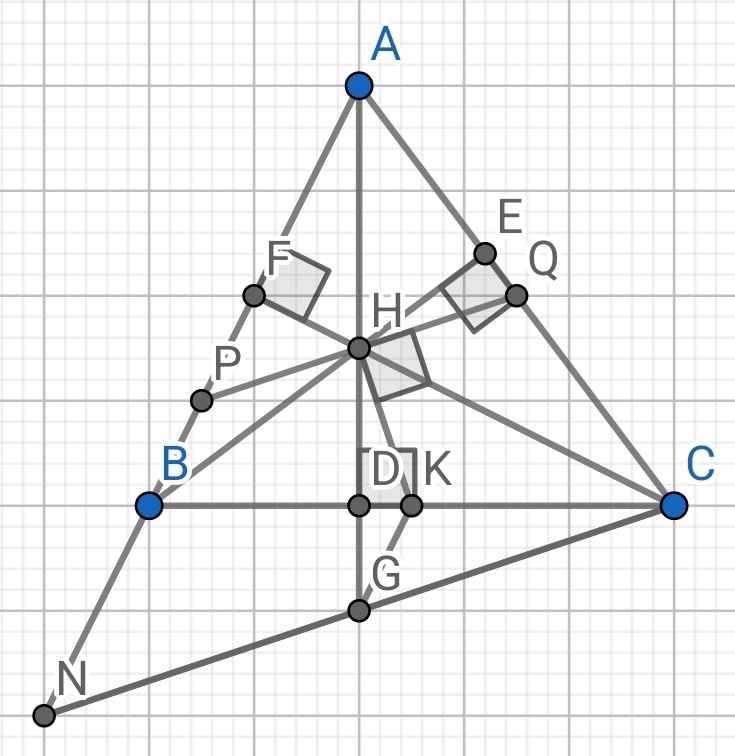
a) Xét hai tam giác vuông: \(\Delta ABC\) và \(\Delta HBA\) có:

\(\widehat{B}\) chung

\(\Rightarrow\Delta ABC\)  ∽\(\Delta HBA\left(g-g\right)\)

\(\Rightarrow\dfrac{AC}{AH}=\dfrac{BC}{AB}\)

\(\Delta ABC\) vuông tại A (gt)

\(\Rightarrow BC^2=AB^2+AC^2\left(Pythagore\right)\)

\(=9^2+12^2\)

\(=225\)

\(\Rightarrow BC=15\left(cm\right)\)

\(\Rightarrow\dfrac{12}{AH}=\dfrac{15}{9}\)

\(\Rightarrow AH=\dfrac{9.12}{15}=7,2\left(cm\right)\)

b) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta CHA\) có:

\(\widehat{BAH}=\widehat{ACH}\) (cùng phụ \(\widehat{ABC}\))

\(\Rightarrow\Delta AHB\)  ∽\(\Delta CHA\left(g-g\right)\)

\(\Rightarrow\dfrac{AH}{CH}=\dfrac{HB}{AH}\)

\(\Rightarrow AH^2=HB.HC\)

c) Do \(\Delta ABC\)  ∽\(\Delta HBA\left(cmt\right)\)

\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)

\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=5,4\left(cm\right)\)

Do \(BE\) là tia phân giác của \(\widehat{ABC}\) (gt)

\(\Rightarrow\widehat{ABE}=\widehat{CBE}\)

\(\Rightarrow\widehat{ABE}=\widehat{HBF}\)

Xét hai tam giác vuông: \(\Delta ABE\) và \(\Delta HBF\) có:

\(\widehat{ABE}=\widehat{HBF}\left(cmt\right)\)

\(\Rightarrow\Delta ABE\)  ∽\(\Delta HBF\left(g-g\right)\)

\(\Rightarrow\dfrac{S_{ABE}}{S_{HBF}}=\left(\dfrac{AB}{HB}\right)^2=\left(\dfrac{9}{7,2}\right)^2=\dfrac{25}{16}\)

a) Xét hai tam giác vuông: ∆BHF và ∆CHE có:

∠BHF = ∠CHE (đối đỉnh)

⇒ ∆BHF ∽ ∆CHE (g-g)

b) Xét hai tam giác vuông: ∆AFC và ∆AEB có:

∠A chung

⇒ ∆AFC ∽ ∆AEB (g-g)

⇒ AF/AE = AC/AB

⇒ AF.AB = AE.AC

c) Sửa đề. Đường thẳng vuông góc với HK tại H cắt AB và AC lần lượt tại P và Q

Giải

Qua C vẽ đường thẳng song song với PQ cắt AB, AD lần lượt tại N và G

⇒ CN // PQ

Mà PQ ⊥ HK

⇒ CN ⊥ HK

⇒ CG ⊥ HK

⇒ HK là đường cao của ∆CHG

Lại có:

BC ⊥ AD (gt)

⇒ CD ⊥ HG

⇒ CD là đường cao thứ hai của ∆CHG

Mà CD cắt HK tại K

⇒ GK là đường cao thứ ba của ∆CHG

⇒ GK ⊥ CH

Mà CH ⊥ AB (gt)

⇒ GK // AB

⇒ GK // BN

∆BCN có:

K là trung điểm của BC (gt)

GK // BN (cmt)

⇒ G là trung điểm của CN

⇒ CG = NG

Do PQ // CN

⇒ PH // NG và QH // CG

∆ANG có:

PH // NG (cmt)

⇒ HP/NG = AH/AG (hệ quả định lý Thales) (1)

∆ACG có:

HQ // CG (cmt)

⇒ HQ/CG = AH/AG (2)

Từ (1) và (2) ⇒ HP/NG = HQ/CG

Mà CG = NG (cmt)

⇒ HP = HQ

Gọi vận tốc thật của cano là x(km/h)

(Điều kiện: x>2)

vận tốc lúc đi là x+2(km/h)

Vận tốc lúc về là x-2(km/h)

\(1h10p=\dfrac{7}{6}\left(giờ\right);1h30p=1,5\left(giờ\right)\)

Độ dài quãng đường lúc đi là \(\dfrac{7}{6}\left(x+2\right)\left(km\right)\)

Độ dài quãng đường lúc về là 1,5(x-2)(km)

Do đó, ta có phương trình:

\(\dfrac{7}{6}\left(x+2\right)=1,5\left(x-2\right)\)

=>\(\dfrac{7}{6}x+\dfrac{7}{3}=1,5x-3\)

=>\(\dfrac{7}{6}x-1,5x=-3-\dfrac{7}{3}\)

=>\(-\dfrac{1}{3}x=-\dfrac{16}{3}\)

=>x=16(nhận)

Vậy: Độ dài quãng đường AB là:

\(\dfrac{7}{6}\left(16+2\right)=\dfrac{7}{6}\cdot18=21\left(km\right)\)

                             Giải

1 giờ 10 phút = \(\dfrac{7}{6}\) giờ; 1 giờ 30 phút = 1,5 giờ

Cứ một giờ ca nô xuôi dòng được: 1 : \(\dfrac{7}{6}\) = \(\dfrac{6}{7}\)(quãng sông)

Cứ một giờ ca nô ngược dòng được: 1 : 1,5  = \(\dfrac{2}{3}\)(quãng sông)

2 km ứng với phân số là: (\(\dfrac{6}{7}\) - \(\dfrac{2}{3}\)): 2 = \(\dfrac{2}{21}\) (quãng sông)

Quãng sông AB dài là: 2 : \(\dfrac{2}{21}\)  = 21 (km)

Kết luận: quãng sông AB dài 21 km. 

a: Xét ΔAIB vuông tại I và ΔAEC vuông tại E có

\(\widehat{IAB}\) chung

Do đó: ΔAIB~ΔAEC

=>\(\dfrac{AI}{AE}=\dfrac{AB}{AC}\)

=>\(AI\cdot AC=AB\cdot AE\)

b: Xét ΔCBI vuông tại I và ΔACF vuông tại F có

\(\widehat{BCI}=\widehat{CAF}\)(BC//AF)

Do đó: ΔCBI~ΔACF

=>\(\dfrac{AF}{CI}=\dfrac{AC}{CB}\)

=>\(AF\cdot CB=CI\cdot CA\)

\(AB\cdot AE+AF\cdot CB\)

\(=AI\cdot AC+CI\cdot AC\)

\(=AC\cdot\left(AI+CI\right)=AC^2\)

a: Để hàm số y=(m+1)x-3 là hàm số bậc nhất thì \(m+1\ne0\)

=>\(m\ne-1\)

b: Để đồ thị hàm số y=(m+1)x-3 song song với đường thẳng y=2x thì \(\left\{{}\begin{matrix}m+1=2\\-3\ne0\left(đúng\right)\end{matrix}\right.\)

=>m+1=2

=>m=1(nhận)

Khi m=1 thì y=(1+1)x-3=2x-3

Vẽ đồ thị:

a: ΔMNP vuông tại M

=>\(MN^2+MP^2=NP^2\)

=>\(NP=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét ΔHMN vuông tại H và ΔHPM vuông tại H có

\(\widehat{HMN}=\widehat{HPM}\left(=90^0-\widehat{MNH}\right)\)

Do đó: ΔHMN~ΔHPM

b: Xét ΔNHM vuông tại H và ΔNMP vuông tại M có

\(\widehat{HNM}\) chung

Do đó: ΔNHM~ΔNMP

=>\(\dfrac{NH}{NM}=\dfrac{NM}{NP}\)

=>\(NM^2=NH\cdot NP\left(1\right)\)
Ta có: PE+NE=NP

=>NE+4=10

=>NE=6(cm)

=>NE=NM(2)

TỪ (1),(2) suy ra \(NE^2=NH\cdot NP\)

Gọi độ dài quãng đường AB là x(km)

(Điều kiện: x>0)

Thời gian người đó đi từ A đến B là \(\dfrac{x}{40}\left(giờ\right)\)

Thời gian người đó đi từ B về A là \(\dfrac{x}{36}\left(giờ\right)\)

Thời gian đi ít hơn thời gian về là 10p=1/6 giờ nên ta có:

\(\dfrac{x}{36}-\dfrac{x}{40}=\dfrac{1}{6}\)

=>\(\dfrac{10x-9x}{360}=\dfrac{1}{6}\)

=>\(\dfrac{x}{360}=\dfrac{1}{6}\)
=>\(x=\dfrac{360}{6}=60\left(nhận\right)\)

vậy: Độ dài quãng đường AB là 60km

Gọi độ dài quãng đường AB là x (km) với x>0

Thời gian xe đi từ A đến B là: \(\dfrac{x}{40}\) giờ

Thời gian xe đi từ B về A là: \(\dfrac{x}{36}\) giờ

Do thời gian đi ít hơn thời gian về là 10 phút =1/6 giờ nên ta có pt:

\(\dfrac{x}{36}-\dfrac{x}{40}=\dfrac{1}{6}\)

\(\Leftrightarrow x\left(\dfrac{1}{36}-\dfrac{1}{40}\right)=\dfrac{1}{6}\)

\(\Leftrightarrow\dfrac{x}{360}=\dfrac{1}{6}\)

\(\Rightarrow x=60\left(km\right)\)

Đề chính xác hơn là \(ab+bc+ca\le\dfrac{1}{3}\)