 Giúp em vs ạ,em cảm ơn trước
Giúp em vs ạ,em cảm ơn trước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi giá ban đầu của 1 đôi giày là x (ngàn đồng) với x>0
Số tiền anh phải trả cho đôi thứ hai là: \(x.\left(100\%-30\%\right)=0,7x\) (ngàn đồng)
Số tiền anh phải trả cho đôi thứ 3 là: \(\dfrac{x}{2}=0,5x\) (ngàn đồng)
Tổng số tiền anh phải trả cho cả 3 đôi giày là:
\(x+0,7x+0,5x=2,2x\) (ngàn đồng)
Do anh phải trả tổng cộng 1320 ngàn đồng nên ta có pt:
\(2,2x=1320\)
\(\Leftrightarrow x=600\) (ngàn đồng) hay \(600000\) đồng

Do đi 10km phải trả 30000, thay vào hàm số ta được:
\(30000x+b=10\) (1)
Do đi 15km phải trả 40000 đồng, thay vào hàm số ta được:
\(40000x+b=15\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}30000a+b=10\\40000a+b=15\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2000}\\b=-5\end{matrix}\right.\)

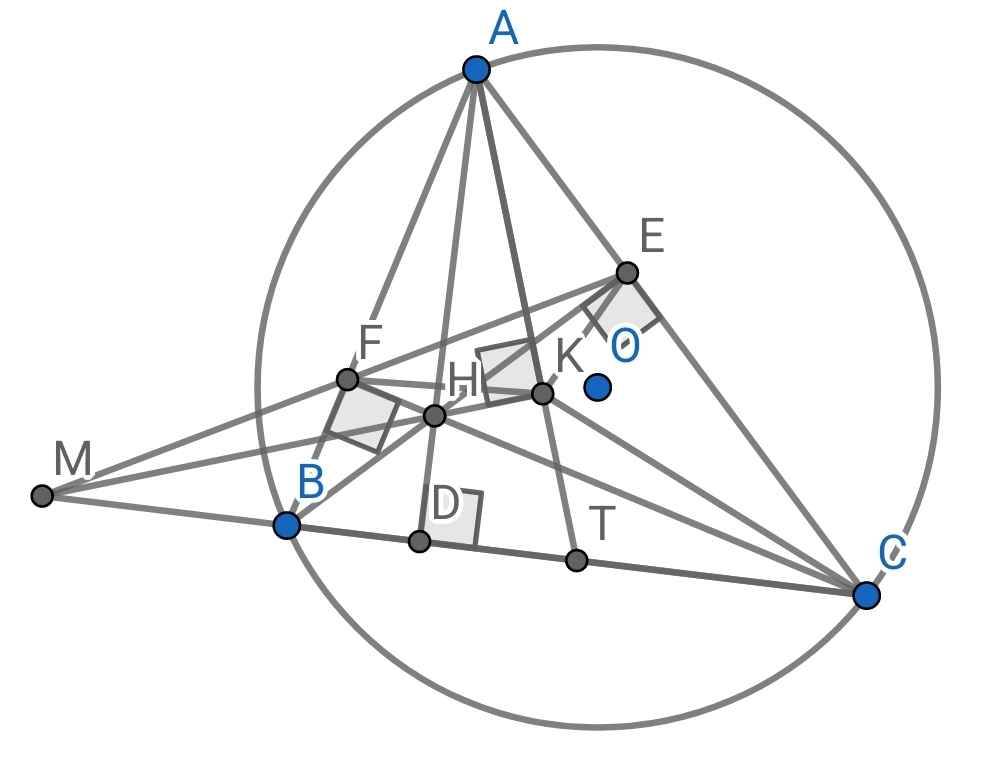
a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
ΔODE cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)DE
Xét tứ giác ABKO có \(\widehat{ABO}=\widehat{AKO}=90^0\)
nên ABKO là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{ABD}\) là góc tạo bởi tiếp tuyến BA và dây cung BD
\(\widehat{BED}\) là góc nội tiếp chắn cung BD
Do đó: \(\widehat{ABD}=\widehat{BED}\)
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot OA=AB^2\left(3\right)\)
Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
DO đó: ΔABD~ΔAEB
=>\(\dfrac{AB}{AE}=\dfrac{AD}{AB}\)
=>\(AB^2=AE\cdot AD\left(4\right)\)
Từ (3),(4) suy ra \(AH\cdot AO=AE\cdot AD\)
c.
Do I là giao điểm 2 tiếp tuyến tại C và D, theo t/c hai tiếp tuyến cắt nhau ta có:
\(\widehat{DOI}=\widehat{COI}\Rightarrow\widehat{DOI}=\dfrac{1}{2}\widehat{DOC}\) (1)
Gọi F là giao điểm BD và OQ
Ta có: \(QB=QD\) (do Q là giao 2 tiếp tuyến tại B và D)
\(OB=OD=R\)
\(\Rightarrow OQ\) là trung trực của BD \(\Rightarrow OQ\perp BD\) tại F
\(\Rightarrow\widehat{BFO}=\widehat{BHO}=90^0\Rightarrow BFHO\) nội tiếp
\(\Rightarrow\widehat{CBD}=\widehat{HOF}\) (cùng chắn HF) (2)
Mà \(\widehat{CBD}=\dfrac{1}{2}\widehat{DOC}\) (góc nt và góc ở tâm cùng chắn DC của (O)) (3)
(1);(2);(3) \(\Rightarrow\widehat{HOF}=\widehat{DOI}\)
\(\Rightarrow\widehat{QOD}+\widehat{DOH}=\widehat{AOI}+\widehat{DOH}\)
\(\Rightarrow\widehat{QOD}=\widehat{AOI}\) (đpcm)

Gọi số học sinh lớp 9a trong kì 1 là x(bạn)
(ĐK: \(x\in Z^+\))
Số học sinh lớp 9b trong kì 1 là 90-x(bạn)
Tổng số học sinh trong kì 2 là 90-2=88(bạn)
Số học sinh lớp 9A kì 2 là x-4(bạn)
Số học sinh lớp 9b kì 2 là 90-x+4-2=92-x(bạn)
Số học sinh lớp 9A kì 2 bằng 5/6 lần số học sinh lớp 9b nên ta có phương trình:
\(x-4=\dfrac{5}{6}\left(92-x\right)\)
=>x=44(nhận)
Vậy: Số học sinh lớp 9a kì 1 là 44 bạn
số học sinh lớp 9b kì 1 là 90-44=46 bạn

Đặt \(\left(a;2b;3c\right)=\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}x;y;z\ge0\\x+y+z=1\end{matrix}\right.\)
\(M=xy-yz+zx\)
Ta có:
\(4M+1=4\left(xy-yz+zx\right)+\left(x+y+z\right)^2\)
\(=6xy+6zx+x^2+y^2+z^2-2yz\)
\(=\left(y-z\right)^2+x\left(6y+6z+x\right)\ge0\) (do \(x;y;z\ge0\))
\(\Rightarrow4M+1\ge0\)
\(\Rightarrow M\ge-\dfrac{1}{4}\)
\(M_{min}=-\dfrac{1}{4}\) khi \(\left\{{}\begin{matrix}x+y+z=1\\x=0\\y=z\end{matrix}\right.\) \(\Rightarrow\left(x;y;z\right)=\left(0;\dfrac{1}{2};\dfrac{1}{2}\right)\) hay \(\left(a;b;c\right)=\left(0;\dfrac{1}{4};\dfrac{1}{6}\right)\)

Sửa đề: |x1|-|x2|=4
Phương trình hoành độ giao điểm là:
\(x^2=mx+m+1\)
=>\(x^2-mx-m-1=0\)(1)
\(\Delta=\left(-m\right)^2-4\cdot1\cdot\left(-m-1\right)\)
\(=m^2+4m+4=\left(m+2\right)^2\)
Để (P) cắt (d) tại hai điểm phân biệt thì \(\Delta>0\)
=>(m+2)^2>0
=>m+2<>0
=>m<>-2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m\\x_1x_2=\dfrac{c}{a}=-m-1\end{matrix}\right.\)
\(\left|x_1-x_2\right|=4\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=4\)
=>\(\sqrt{m^2-4\left(-m-1\right)}=4\)
=>\(\sqrt{\left(m+2\right)^2}=4\)
=>|m+2|=4
=>\(\left[{}\begin{matrix}m+2=4\\m+2=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=2\\m=-6\end{matrix}\right.\)(2)
Khi m<>-2 thì phương trình (1) luôn có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{m-\sqrt{\left(m+2\right)^2}}{2}=\dfrac{m-m-2}{2}=-1\\x=\dfrac{m+\sqrt{\left(m+2\right)^2}}{2}=\dfrac{m+m+2}{2}=m+1\end{matrix}\right.\)
\(\left|x_1\right|-\left|x_2\right|=4\)
=>\(\left[{}\begin{matrix}\left|-1\right|-\left|m+1\right|=4\\\left|m+1\right|-\left|-1\right|=4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left|m+1\right|=1-4=-3\left(loại\right)\\\left|m+1\right|=4+1=5\end{matrix}\right.\)
=>|m+1|=5
=>\(\left[{}\begin{matrix}m=4\\m=-6\end{matrix}\right.\)(3)
Từ (2),(3) suy ra m=-6




a.
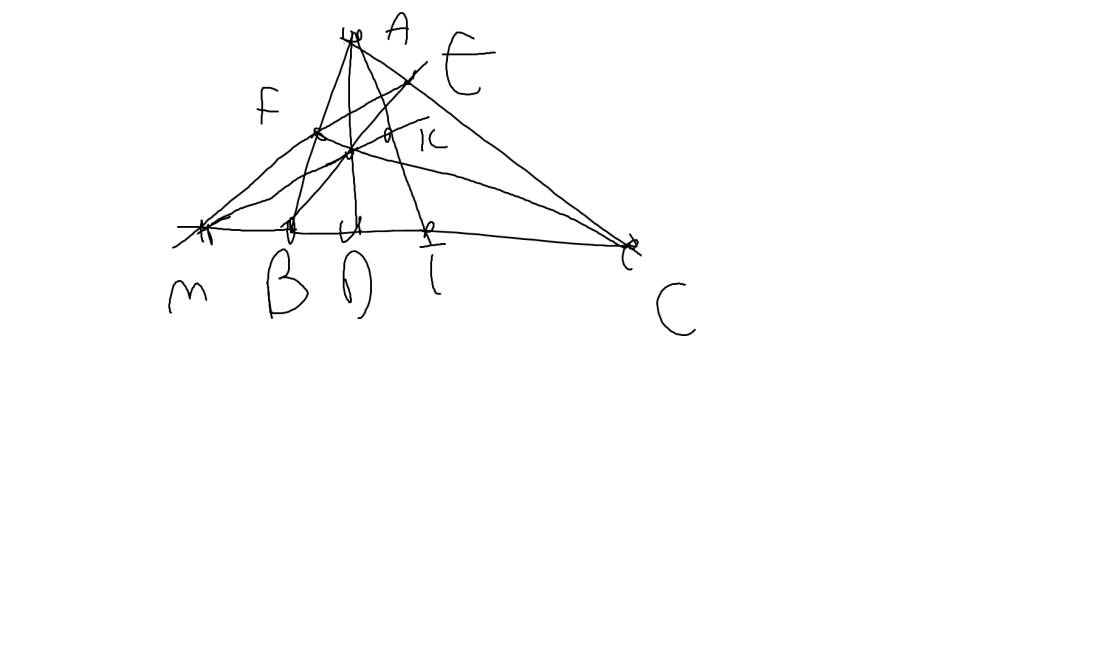
Do MA, MB là các tiếp tuyến \(\Rightarrow\widehat{MAO}=\widehat{MBO}=90^0\)
\(\Rightarrow A,B\) cùng nhìn OM dưới 1 góc vuông nên AOBM nội tiếp
b.
\(C_{\left(O\right)}=2\pi R=10\pi=31,42\left(cm\right)\)
Trong tam giác vuông OAM:
\(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AOB}=2\widehat{AOM}=120^0\)
\(\Rightarrow S_{OAB}=S_{\left(O\right)}.\dfrac{120}{360}=\dfrac{\pi.R^2}{3}=\dfrac{5^2.\pi}{3}\approx26,18\)
c.
Ta có \(CM=OM-OC=2R-R=R\)
\(\Rightarrow CM=OC\Rightarrow C\) là trung điểm OM
\(\Rightarrow AC\) là trung tuyến ứng với cạnh huyền trong tam giác vuông OAM
\(\Rightarrow AC=\dfrac{1}{2}OM=R=OA\)
Tương tự có BC là trung tuyến ứng với cạnh huyền trong tam giác vuông OBM
\(\Rightarrow BC=OC=R\)
\(\Rightarrow OA=AC=BC=OB\Rightarrow AOBC\) là hình thoi
Gọi D là giao điểm AB và OC \(\Rightarrow AD\perp OC\) (hai đường chéo hình thoi)
Trong tam giác vuông AOD:
\(sin\widehat{AOD}=\dfrac{AD}{OA}\Rightarrow AD=OA.sin\widehat{AOD}=5.sin60^0=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
\(\Rightarrow AB=2AD=5\sqrt{3}\) (cm)
\(\Rightarrow S_{AOBC}=\dfrac{1}{2}AD.OC=\dfrac{25\sqrt{3}}{2}\approx21,65\left(cm^2\right)\)