(1/2-1/3)-(5/3-3/2)+(7/3-5/2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{45}\\\dfrac{y}{2}-\dfrac{x}{2}=28\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{45}\\\dfrac{y}{2}=\dfrac{x}{2}+28\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{x+56}=\dfrac{1}{45}\\y=x+56\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}45\left(x+56\right)+45x=x\left(x+56\right)\\y=x+56\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}90x+2520=x^2+56x\\y=x+56\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x^2-34x-2520=0\\y=x+56\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=70\\x=-36\end{matrix}\right.\\y=x+56\end{matrix}\right.\)
Khi x = 70 => y = 70 + 56 = 126
Khi x = -36 => y = (-36) + 56 = 20

Sửa đề: B là giao điểm có hoành độ dương của (P) và (d)
Phương trình hoành độ giao điểm của (P) và (d):
−x² = x − 2
x² + x − 2 = 0
x² − x + 2x − 2 = 0
(x² − x) + (2x − 2) = 0
x(x − 1) + 2(x− 1) = 0
(x − 1)(x + 2) = 0
x − 1 = 0 hoặc x + 2 = 0
*) x − 1 = 0
x = 1
y = −1² = −1
B(1; −1)
*) x + 2 = 0
x = −2
y = −(−2)² = −4
A(−2; −4)
* Phương trình đường thẳng OB:
Gọi (d'): y = ax + b là phương trình đường thẳng OB
Do (d') đi qua O nên b = 0
=> (d'): y = ax
Do (d') đi qua B(1; −1) nên:
a = −1
=> (d'): y = −x
Gọi (d''): y = a'x + b' là đường thẳng đi qua A(−2; −4)
Do (d'') // (d') nên a' = −1
=> (d''): y = −x + b
Do (d'') đi qua A(−2; −4) nên:
−(−2) + b = −4
b = −4 − 2
b = −6
=> (d''): y = −x − 6

Giải:
Gọi số nhỏ thoả mãn đề bài là \(x\); \(x\) \(\in\) N
Số thứ hai là: \(x\) + 1
Số thứ ba là: \(x\) + 1 + 1
Tổng của ba số là: \(x\) + \(x\) + 1 + \(x\) + 1 + 1 = 3\(x\) + 3
Theo bài ra ta có: 3\(x\) + 3 = 483
3\(x\) = 483 - 3
3\(x\) = 480
\(x\) = 480 : 3
\(x\) = 160
Vậy số nhỏ nhất thoả mãn đề bài là: 160
Trung bình cộng của 3 số tự nhiên liên tiếp x-1,x,x+1, xϵN* là:
x = 483/3 = 161
vậy, số nhỏ nhất là 160




Giải:
+ Xét hạng tử thứ nhất là: 5\(x^3\) vậy hạng tử này có bậc là 3
+ Xét hạng tử thứ hai là: \(xy^2z^3\)
\(x\) có bậc là 1
y2 có bậc là 2
z3 có bậc là 3
Vậy hạng tử \(xy^2z^3\) có bậc là: 1 + 2 + 3 = 6
+ Bậc của hạng tử \(xy^2z^3\) lớn hơn bậc của hạng tử - 5\(x^3\) nên đó là bậc của đa thức vì vậy bậc của đa thức là 6

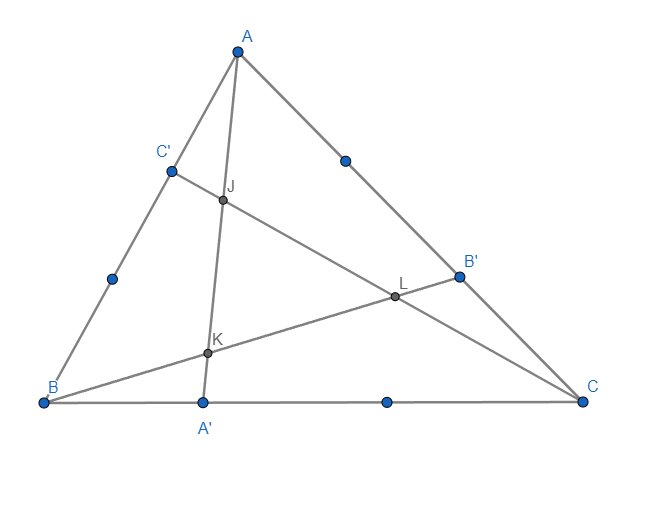
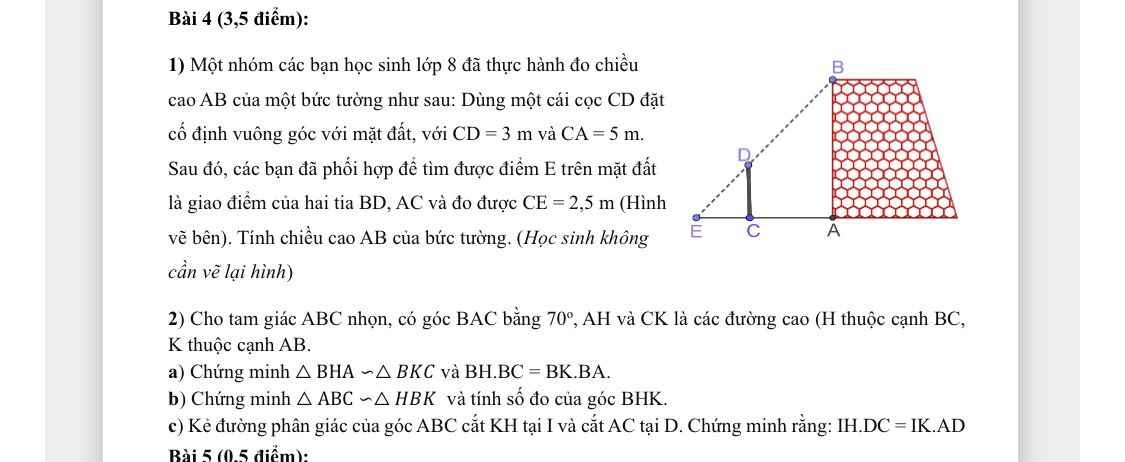
2:
a: Xét ΔBHA vuông tại H và ΔBKC vuông tại K có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBKC
=>\(\dfrac{BH}{BK}=\dfrac{BA}{BC}\)(2)
=>\(\dfrac{BH}{BA}=\dfrac{BK}{BC}\)
=>\(BH\cdot BC=BK\cdot BA\)
b: Xét ΔBHK và ΔBAC có
\(\dfrac{BH}{BA}=\dfrac{BK}{BC}\)
\(\widehat{HBK}\) chung
Do đó: ΔBHK~ΔBAC
=>\(\widehat{BHK}=\widehat{BAC}=70^0\)
c: Xét ΔBKH có BI là phân giác
nên \(\dfrac{IH}{IK}=\dfrac{BH}{BK}\left(1\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{IH}{IK}=\dfrac{DA}{DC}\)
=>\(IH\cdot DC=DA\cdot IK\)
\(\left(\dfrac{1}{2}-\dfrac{1}{3}\right)-\left(\dfrac{5}{3}-\dfrac{3}{2}\right)+\left(\dfrac{7}{3}-\dfrac{5}{2}\right)\\ =\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{5}{3}+\dfrac{3}{2}+\dfrac{7}{3}-\dfrac{5}{2}\\ =\left(\dfrac{1}{2}+\dfrac{3}{2}-\dfrac{5}{2}\right)+\left(-\dfrac{1}{3}-\dfrac{5}{3}+\dfrac{7}{3}\right)\\ =-\dfrac{1}{2}+\dfrac{1}{3}\\ =-\dfrac{1}{6}\)