(3 điểm) Cho đường tròn $\left( O \right)$ và điểm $A$ nằm ngoài đường tròn. Qua điểm $A$ kẻ hai tiếp tuyến $AB$ và $AC$ đến $\left( O \right)$ ($B,\,C$ là các tiếp điểm). Kẻ tia ${Ax}$ (nằm giữa hai tia ${AB, AO}$) cắt đường tròn tại $E$ và $F$ ($E$ nằm giữa $A$ và $F$ ) .
a) Chứng minh rằng tứ giác $ABOC$ nội tiếp đường tròn.
b) Chứng minh rằng $B{{A}^{2}}=AE.{AF}$ và $\widehat{{OEF}}=\widehat{{OHF}}$, với $H$ là giao điểm của $AO$ và $BC$.
c) Đường thẳng qua $E$ song song với $BF$ cắt đường thẳng $BC$ tại $K{.}$ Đường thẳng $AK$ cắt đường thẳng $BF$ tại $M.$ Chứng minh rằng $MC=2HF.$

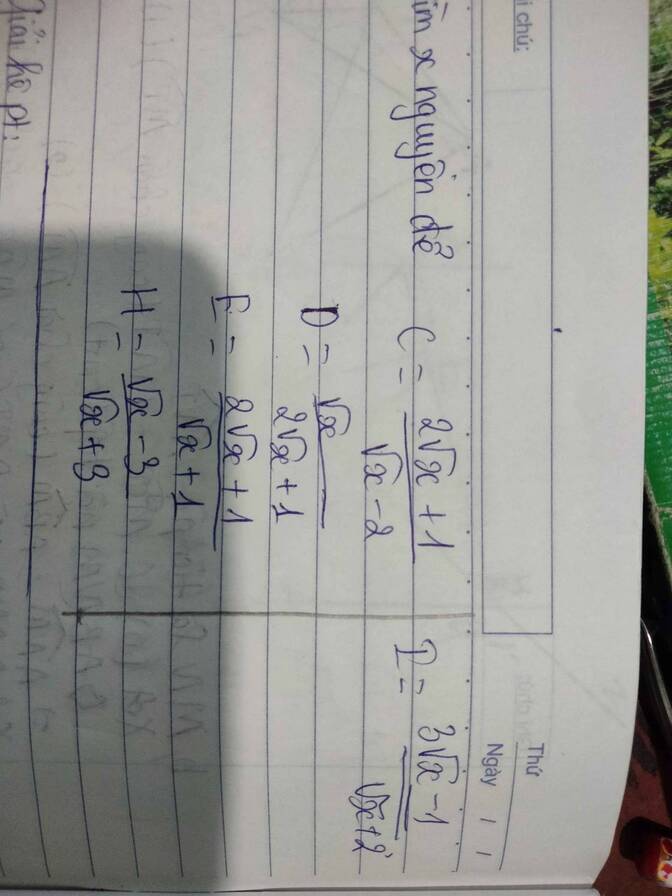 Tìm x để bt nguyê
Tìm x để bt nguyê