a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)

nên AEHF là tứ giác nội tiếp

b: Ta có; ΔFBC vuông tại F

mà FO là đường trung tuyến

nên OF=OC

=>ΔOFC cân tại O

=>\(\widehat{OFC}=\widehat{OCF}\)

mà \(\widehat{OCF}=\widehat{BAD}\left(=90^0-\widehat{ABC}\right)\)

nên \(\widehat{OFC}=\widehat{BAD}\)

c) Gọi J là trung điểm OH. Vẽ đường tròn đường kính OH. Khi đó vì \(\widehat{ODH}=90^o\) nên \(D\in\left(J\right)\). Vẽ đường tròn (BC)

 Xét tam giác AEH và ADC, ta có: \(\widehat{AEH}=\widehat{ADC}=90^o\) và \(\widehat{HAC}\) chung \(\Rightarrow\Delta AEH\sim\Delta ADC\) 

\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AH}{AC}\) 

\(\Rightarrow AE.AC=AD.AH\)

\(\Rightarrow P_{A/\left(O\right)}=P_{A/\left(J\right)}\)

\(\Rightarrow\) A nằm trên trục đẳng phương của (O) và (J).

Mặt khác, trong đường tròn (O), ta có: \(\widehat{FOE}=2\widehat{FCE}=\widehat{HCE}+\widehat{HBF}\) \(=\widehat{HDE}+\widehat{HDF}=\widehat{FDE}\) nên tứ FDOE nội tiếp.

 \(\Rightarrow\widehat{FOD}=\widehat{FED}\)

 Xét tam giác MDE và MFO, ta có:

 \(\widehat{MED}=\widehat{MOF},\widehat{EMO}\) chung 

 \(\Rightarrow\Delta MDE\sim\Delta MFO\left(g.g\right)\)

 \(\Rightarrow\dfrac{MD}{MF}=\dfrac{ME}{MO}\)

 \(\Rightarrow MD.MO=MF.ME\)

 \(\Rightarrow P_{M/\left(J\right)}=P_{M/\left(O\right)}\)

 \(\Rightarrow\) M thuộc trục đẳng phương của (J) và (O)

Do đó AM là trục đẳng phương của (O) và (J) \(\Rightarrow AM\perp OJ\) hay \(AM\perp OH\) 

 Lại có \(AH\perp OM\) nên H là trực tâm tam giác AOM \(\Rightarrow MH\perp AO\) (đpcm)

Bạn giải 10 bài không bằng bạn chỉ giải 2,3 bài nhưng sau khi giải bạn đầu tư thời gian để tư duy: Cách phát hiện Dạng bài (thể loại bài), Những lưu ý quan trọng để giải quyết dạng bài (keys), Những biến dạng của thể loại bài...

Cái mà bạn đề cập đến nó thuộc phương pháp giải. Trong toán học gọi là "phương pháp ĐẶT ẨN". Một trong những lưu ý cốt tử là: Chọn đối tượng nào làm ẩn để tối ưu nhất khi ta thiết lập phương trình từ những dữ kiện mà bài đã cho. Và một trong những điều học trò rất hay quên (nên kg được điểm tối đa) là sau khi đặt ẩn, lại quên nêu phạm vi và đơn vị của ẩn.

Ví dụ: Sau khi "Đặt vận tốc dự kiến của Xe A là X" thì quên mất mở ngoặc: X>0, đơn vị km/h hoặc km/g

Gợi ý cho bạn trình tự giải bài này:

1/. Với khuyến mại (dùng khuyến mãi là sai nhé) của siêu thị (mua 4 tặng 1) thì số chai sữa tắm phải trả tiền là: S (chai). Từ đó tính ra được số tiền phải trả cho Sữa tắm là Ts=S.39 nghìn đồng (Ts: Tức là Tiền Sữa tắm).

2/. Vậy số tiền phải trả cho Bột giặt và Dầu gội còn lại là T2 (nghìn đồng).

         T2=2119 - Ts (nghìn đồng).

3/. Đặt giá niêm yết của Dầu gội là X (nghìn đồng)/chai, thì giá niêm yết của Bột giặt là (X+105) nghìn đồng /chai.

4/. Với khuyến mại (KM) bột giặt ta thấy: Số tiền phải trả so với giá niêm yết giảm 50.000 đ (vì Chỉ có 2 túi là phải trả theo giá niêm yết, 5 túi còn lại đc giảm 10.000đ/túi). Và số tiền phải trả cho Bột giặt là: Tb=7.(X+105) - 50 = 7.X + 685 (nghìn đồng). Tb có nghĩa là Tiền bột giặt.

5/. Tương tự, với KM dầu gội: Chỉ có 2 chai phải trả theo giá niêm yết, 6 chai được giảm 15% (tức là phải trả 85%). Vậy số tiền phải trả cho dầu gội là:

Td=2.X+6.X.85% = 7,1.X (nghìn đồng).  Td nghĩa là Tiền dầu gội.

6/. Ta có T2=Tb+Td = (7.X+685) + (7,1.X) ===> Tính ra được X.

Số chai sữa tắm chị Hồng mua là: \(15:(4+1).4=12(chai)\)

Số tiền sữa tắm là: \(12 \times 39000=468000(đồng)\)

Số tiền mua bột giặt và dầu gội là: \(2119000-468000=1651000(đồng)\)

Gọi giá bột giặt và dầu gội lần lượt là a và b (a,b >0)

Ta có : \(a - b = 105000 (đồng)\)(1)

Giá sau khi giảm của dầu gội là: 0,85b (đồng)

Số tiền mua dầu gội là: \(0,85.8.b=6,8b(đồng)\)

Số tiền mua bột giặt là: \(2a + (a-10000).5=7a-50000(đồng)\)

=> Ta có: \(6,8b+7a-50000=1651000(đồng)\)(2)

Từ 1 và 2 ta có:

\(\left\{{}\begin{matrix}a-b=105000\\7a+6,8b=1701000\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}7a-7b=735000\\7a+6,8b=1701000\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}13,8b=966000\\a-b=105000\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}b=70000\\a=175000\end{matrix}\right.\)(tmđk)

Vậy giá niêm yết của bột giặt và dầu gội lần lượt là 175000 đồng và 70000đồng

nhẩm được một nghiệm x=1

sử dụng sơ đồ hoocne

8: Gọi thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là x(giờ) và y(giờ)

(Điều kiện: x>0; y>0)

Trong 1 giờ, người 1 làm được \(\dfrac{1}{x}\)(công việc)

Trong 1 giờ, người 2 làm được \(\dfrac{1}{y}\)(công việc)

7h12p=7,2(giờ)

Trong 1 giờ, hai người làm được \(\dfrac{1}{7,2}=\dfrac{5}{36}\)(công việc)

Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\left(1\right)\)

Trong 4 giờ, người 1 làm được \(\dfrac{4}{x}\)(công việc)

Trong 3 giờ, người 2 làm được \(\dfrac{3}{y}\)(công việc)

Nếu người 1 làm trong 4 giờ và người 2 làm trong 3 giờ thì hai người làm được 50% công việc nên \(\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\left(2\right)\)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{5}{9}-\dfrac{1}{2}=\dfrac{1}{18}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=18\\\dfrac{1}{x}=\dfrac{5}{36}-\dfrac{1}{18}=\dfrac{5-2}{36}=\dfrac{1}{12}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=12\\y=18\end{matrix}\right.\left(nhận\right)\)

Vậy: thời gian người 1 và người 2 hoàn thành công việc khi làm một mình lần lượt là 12 giờ=0,5 ngày và 18 giờ=0,75 ngày

9:

Gọi chiều dài và chiều rộng lần lượt là a(m) và b(m)

(Điều kiện: a>0; b>0)

Diện tích là 720m² nên ab=720

Nếu tăng chiều dài lên 6m và giảm chiều rộng 4m thì diện tích không đổi nên (a+6)(b-4)=ab

=>ab-4a+6b-24=ab

=>-4a+6b=24

=>2a-3b=-12

=>2a=3b-12

=>a=1,5b-6

ab=720

=>\(b\left(1,5b-6\right)=720\)

=>\(b\left(b-4\right)=720:1,5=480\)

=>\(b^2-4b-480=0\)

=>\(\left[{}\begin{matrix}b=24\left(nhận\right)\\b=-20\left(loại\right)\end{matrix}\right.\)

a=1,5b-6=1,5*24-6=30(nhận)

Vậy: Chiều dài là 30m; chiều rộng là 24m

1. Chứng minh tứ giác OMAN nội tiếp:

Để chứng minh tứ giác OMAN nội tiếp, ta cần chứng minh tổng hai góc đối nhau bằng 180 độ.

Ta có:

• Góc OAN = 90 độ (vì AN là tiếp tuyến của đường tròn tại N)
• Góc OMA = 90 độ (vì AM là tiếp tuyến của đường tròn tại M)

Vậy, góc OAN + góc OMA = 90 độ + 90 độ = 180 độ.

Tương tự, ta cũng có góc MAN + góc MOA = 180 độ.

Vậy, tứ giác OMAN nội tiếp.

2. Tính diện tích phần tứ giác nằm ngoài hình tròn theo R, biết OA = 2R:

Diện tích phần tứ giác nằm ngoài hình tròn là diện tích tam giác OAN trừ đi diện tích phần hình tròn OAN.

Diện tích tam giác OAN = 1/2 * OA * ON = 1/2 * 2R * R = R^2.

Góc AON = 90 độ (vì AN là tiếp tuyến của đường tròn tại N), nên diện tích phần hình tròn OAN = 1/4 * pi * R^2.

Vậy, diện tích phần tứ giác nằm ngoài hình tròn = R^2 - 1/4 * pi * R^2.

Thích bn nhé!

Câu a tự làm;

Câu b:

Hoành độ giao điểm là nghiệm của phương trình: 

\(x^2\) = - 2\(x\) + 3

\(x^2\) + 2\(x\) - 3 = 0

a + b  - c  = 1 + 2  - 3 = 0

Phương trình có hai nghiệm phân biệt là:

  \(x_1\) = 1; \(x_2\) = -3 

\(x_1\) = 1 ⇒ y₁ = (1)² = 1

\(x_2\) = - 3 ⇒ y₂ = (-3)² = 9

Vậy (P) và (d) cắt nhau tai hai điểm có tọa độ lần lượt là:

A(1; 1); B(-3; 9)

a: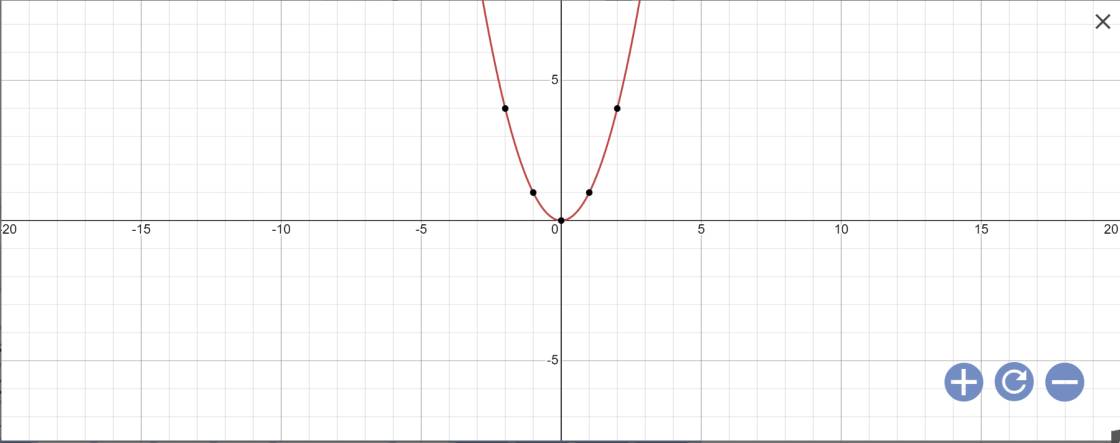 

b: Phương trình hoành độ giao điểm là:

\(x^2=-2x+3\)

=>\(x^2+2x-3=0\)

=>(x+3)(x-1)=0

=>\(\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)

Thay x=-3 vào y=-2x+3, ta được:

\(y=-2\cdot\left(-3\right)+3=9\)

Thay x=1 vào y=-2x+3, ta được:

\(y=-2\cdot1+3=1\)

Vậy: (d) cắt (P) tại A(-3;9); B(1;1)

Do xy=1 nên ta biến đối vế trái để bài toán trở thành Chứng minh BĐT sau:

\(\dfrac{4}{\left(x+y\right)^2}-2\dfrac{2}{\left(x+y\right)}\left(x+y\right)+\left(x^2+2xy+y^2\right)+2\ge3\)

Hay:  \(\dfrac{4}{\left(x+y\right)^2}-2\dfrac{2}{\left(x+y\right)}\left(x+y\right)+\left(x+y\right)^2\ge1\)

<==> \(\left(\dfrac{2}{x+y}-\left(x+y\right)\right)^2\ge1\)  quy đồng mẫu số vế trái:

<==> \(\left(\dfrac{-\left(x^2+y^2\right)}{x+y}\right)^2\ge1\)  (do xy=1)

<==> \(\left(\dfrac{\left(x^2+y^2\right)}{x+y}\right)^2\ge1\)   (*)

(vì vế trái là Bình phương 1 phân số nên ta có thể bỏ qua dấu âm của tử số).

Xét vế trái của (*):

Áp dụng BĐT Bunhiacopxki cho mẫu số: (x+y) ≤ \(\sqrt{2}\cdot\sqrt{x^2+y^2}\)

(Đẳng thức khi x=y)

Khi đó Vế trái BĐT (*) :  \(\left(\dfrac{\left(x^2+y^2\right)}{x+y}\right)^2\ge\left(\dfrac{\left(x^2+y^2\right)}{\sqrt{2\left(x^2+y^2\right)}}\right)^2=\dfrac{\left(x^2+y^2\right)}{2}\)    (**)

Áp dụng BĐT Cô sy cho tử số (cả x² và y² đều là số dương) ta có:

 (x²+y²)  ≥  2xy =2 (do xy=1)  Đẳng thức khi x=y.  ==> (**) ≥1

Đó chính là Đpcm (*). (Đẳng thức khi x=y=1).