Tìm $x,$ $y$ trong hình sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ΔABH vuông tại H có:
AH2 = AB2 - y2 ( Py-ta-go)
⇔BH.HC = AB2 - y2
⇔ 32y = 302 - y2
⇔ 32y + y2 - 900 = 0
⇔ 50y + y2 -18y - 900 = 0
⇔ y(50 + y) - 18( y + 50) = 0
⇔(y -18)(50+y)= 0
⇔\(\left[{}\begin{matrix}y-18=0\\50+y=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}y=18\left(nhận\right)\\y=-50\left(loại\right)\end{matrix}\right.\)
ΔABC vuông tại A có:
x2= BC2 - AB2 ( py-ta-go)
⇔x2= (18 + 32)2 - 302
⇔x2= 1600
⇒x=40
* Áp dụng hệ thức : \(AB^2=BH.BC\)( mà \(BC=BH+HC=BH+32\))
\(\Rightarrow BH=\frac{900}{BH+32}\Rightarrow BH=18\)
hay \(y=18\)
* Áp dụng hệ thức : \(AC^2=HC.BC\)( mà \(BC=HC+BH=32+18=40\))
\(\Rightarrow AC^2=32.40=1280\Rightarrow AC=16\sqrt{5}\)
hay \(x=16\sqrt{5}\)

Áp dụng định lí Py ta go ta có : \(AC^2=AH^2+HC^2\Rightarrow AH^2=AC^2-HC^2\)
\(=100-64=36\Rightarrow AH=6\)cm
* Áp dụng hệ thức \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AB^2}=\frac{1}{AH^2}-\frac{1}{AC^2}\)
\(=\frac{1}{36}-\frac{1}{100}=\frac{100-36}{3600}=\frac{64}{3600}\Rightarrow AB^2=\frac{3600}{64}\Rightarrow AB=\frac{15}{2}\)
hay \(x=\frac{15}{2}\)cm
* Áp dụng hệ thức : \(AH^2=BH.HC\Rightarrow BH=\frac{AH^2}{HC}=\frac{36}{8}=\frac{9}{2}\)
hay \(y=\frac{9}{2}\)cm


Đặt \(A=\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\)
Ta có:
\(x^2+xy+yz+zx=x+xyz=x\left(x+yz\right)\)
\(\Rightarrow\frac{x\left(x+yz\right)}{x}=\frac{x^2+xy+yz+zx}{x}\)
\(\Leftrightarrow x+yz=\frac{x^2+xy+yz+zx}{x}=\frac{\left(x^2+xy\right)+\left(yz+zx\right)}{x}=\frac{\left(x+z\right)\left(x+y\right)}{x}\)
\(\Rightarrow\sqrt{x+yz}=\sqrt{\frac{\left(x+y\right)\left(x+z\right)}{x}}\)
Vì x, y, z >0 nên áp dụng bất đẳng thức Bunhiacopxki cho 2 số dương, ta được:
\(\left(x+y\right)\left(x+z\right)\ge\left(\sqrt{x^2}.+\sqrt{yz}\right)^2\)
\(\Rightarrow\sqrt{\left(x+y\right)\left(x+z\right)}\ge x+\sqrt{yz}\)
\(\Rightarrow\sqrt{\frac{\left(x+y\right)\left(x+z\right)}{x}}\ge\frac{x+\sqrt{yz}}{\sqrt{x}}\)
Do đó \(\sqrt{x+yz}\ge\frac{x+\sqrt{yz}}{\sqrt{x}}\left(1\right)\)
Chứng minh tương tự, ta được:
\(\sqrt{y+xz}\ge\frac{y+\sqrt{xz}}{\sqrt{y}}\left(2\right)\)
Chứng minh tương tự, ta được:
\(\sqrt{z+xy}\ge\frac{z+\sqrt{xy}}{\sqrt{z}}\left(3\right)\)
Từ (1), (2) và (3), ta được:
\(\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\)\(\ge\frac{x+\sqrt{yz}}{\sqrt{x}}+\frac{y+\sqrt{zx}}{\sqrt{y}}+\frac{z+\sqrt{xy}}{\sqrt{z}}\)
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{\frac{yz}{x}}+\sqrt{y}+\sqrt{\frac{xz}{y}}+\sqrt{z}+\sqrt{\frac{xy}{z}}\)
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\frac{yz+zx+xy}{\sqrt{xyz}}\)
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\frac{xyz}{\sqrt{xyz}}\)(vì \(xy+yz+zx=xyz\))
\(\Leftrightarrow A\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\sqrt{xyz}\)(điều phải chứng minh).
Dấu bằng xảy ra.
\(\Leftrightarrow\hept{\begin{cases}x=y=z>0\\xy+yz+zx=xyz\end{cases}}\Leftrightarrow x=y=z=3\)
Vậy với x, y, z là các số thực dương thỏa mãn xy + yz + zx =xyz thì:
\(\sqrt{x+yz}+\sqrt{y+zx}+\sqrt{z+xy}\ge\sqrt{x}+\sqrt{y}+\sqrt{z}+\sqrt{xyz}\).
\(\)


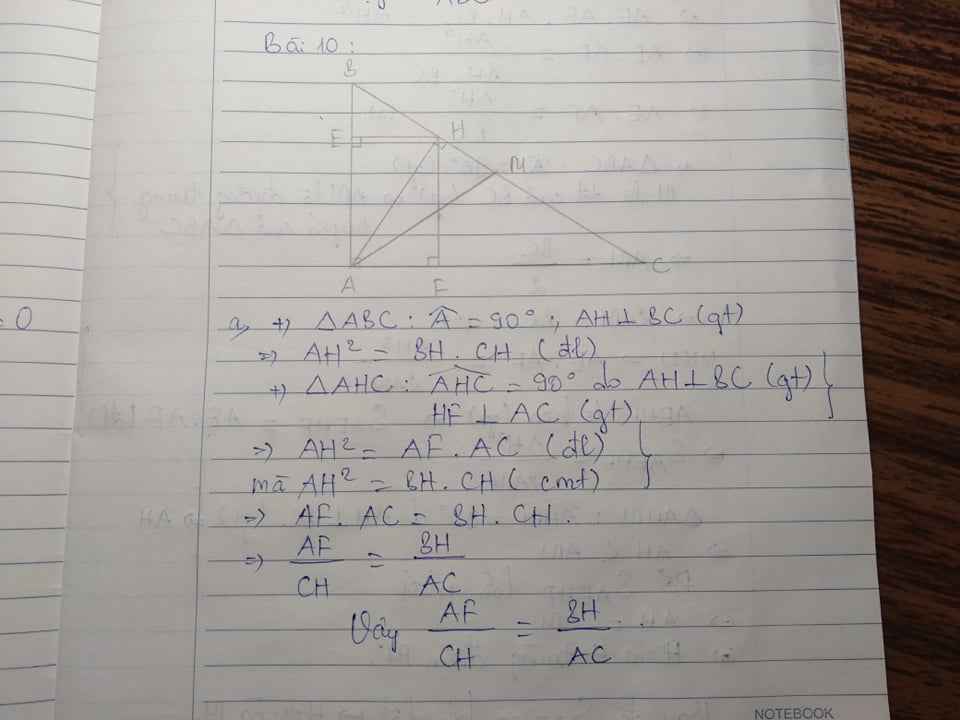
Xét tam giác ABC vuông tại A, có đường cao AH
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=400-144=256\Rightarrow AC=16\)
* Áp dụng hệ thức : \(AC^2=HC.BC\Rightarrow HC=\frac{AC^2}{BC}=\frac{256}{20}=\frac{89}{5}\)
hay \(y=\frac{89}{5}\)
*Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{144}{20}=\frac{36}{5}\)
hay \(x=\frac{36}{5}\)
\(12^2\)=20*x\(\Rightarrow\)x=\(\dfrac{12^2}{20}\)=7,2;
x+y=20\(\Leftrightarrow\)y=20-x\(\Leftrightarrow\)y=20-7,2\(\Leftrightarrow\)y=12,8