Gọi d là ƯCLN của `2n+3` và `4n+7`

Ta có: 

`2n+3` ⋮ d và `4n+7` ⋮ d 

`=>2(2n+3)` ⋮ d và `4n+7` ⋮ d

`=>4n+6` ⋮ d và `4n+7` ⋮ d 

`=>(4n+7)-(4n+6)` ⋮ d 

`=>1` ⋮ d 

`=>d=1` 

Vậy: `2n+3` và `4n+7` là 2 số nguyên tố cùng nhau 

Mọi người giúp em với ạ, bây giờ em đang cần gấp ạ!

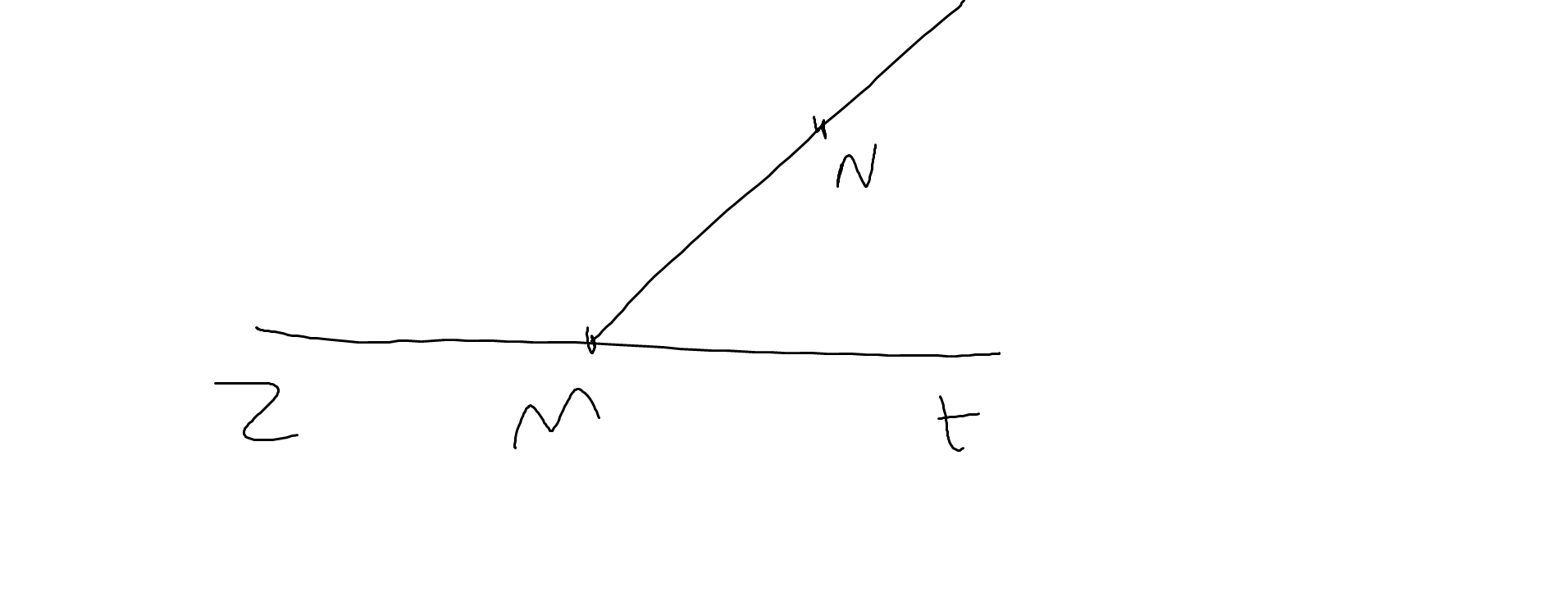
a: Các góc có trong hình vẽ là \(\widehat{tMN};\widehat{zMN};\widehat{tMz}\)

b: Góc bẹt là \(\widehat{tMz}\)

Bài 2:

Xét tam giác ABC vuông tại A ta có:

\(sinC=\dfrac{AB}{BC}=>\dfrac{AB}{BC}=\dfrac{3}{4}\\ =>AB=\dfrac{3}{4}BC=\dfrac{3}{4}\cdot10=\dfrac{15}{2}\left(cm\right)\) 

Áp dụng định lý Pythagore cho tam giác ABC ta có:

\(AB^2+AC^2=BC^2\\ =>\left(\dfrac{15}{2}\right)^2+AC^2=10^2\\ =>AC=\sqrt{10^2-\left(\dfrac{15}{2}\right)^2}=\dfrac{5\sqrt{7}}{2}\left(cm\right)\)

Áp dụng hệ thức lượng ta có:

\(AB^2=BC\cdot BH=>BH=\dfrac{AB^2}{BC}=\left(\dfrac{15}{2}\right)^2:10=\dfrac{225}{40}\left(cm\right)\\ AC^2=BC\cdot CH=>CH=\dfrac{AC^2}{BC}=\left(\dfrac{5\sqrt{7}}{2}\right)^2:10=\dfrac{175}{40}\left(cm\right)\)

Bài 9:

ΔABC vuông tại A

=>\(BC^2=AB^2+AC^2\)

=>\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)

ΔABC vuông tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot9\cdot12=54\left(cm^2\right)\)

Xét ΔABC có AD là phân giác

nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{9}{12}=\dfrac{3}{4}\)

=>\(\dfrac{BD}{BC}=\dfrac{3}{7}\)

=>\(S_{ABD}=54\cdot\dfrac{3}{7}=\dfrac{162}{7}\left(cm^2\right)\)

Một năm đồng hồ đó chạy nhanh hơn khoảng:

\(10\times365=3650\) (giây) 

Một thế kỳ đồng hồ chạy nhanh hơn khoảng: 

\(3650\times10=36500\) (giây)

Đổi: `36500` giây = 10 giờ dư 500 giây  

=> Khoảng 10 giờ 

Vì là ước không bắt buộc là só nguyên tố nên các ước lớn hơn  của 30 là: 10; 15; 30.

Ta có:

`(3x-6)^2022>=0` với mọi x

`(5y+10)^2024>=0` với mọi y

`=>(3x-6)^2022+(5y+10)^2024>=0` với mọi x,y

Mặt khác: `(3x-6)^2022+(5y+10)^2024)<=0` với mọi x,y

Dấu "=" xảy ra: `3x-6=0` và `5y+10=0`

`<=>3x=6` và `5y=-10`

`<=>x=6/3=2` và `y=-10/5=-2` 

\(A=1^2-2^2+3^2-4^2+...+2023^2-2024^2+2025^2\\ =\left(1+2\right)\left(1-2\right)+\left(3+4\right)\left(3-4\right)+\left(2023-2024\right)\left(2023+2024\right)\\ =-3-7-11-...-4047+2025^2\\ =-\left(3+7+11+..+4047\right)+2025^2\)

Xét tổng: `3+7+11+...+4047`

Số lượng số hạng: `(4047-3):4+1=1012` 

Tổng: `(4047+3)*1012/2=2049300` 

`=>A=-2049300+2025^2`

`=>A=-2049300+4100625`

`=>A=2051325` 

Phải bằng cạnh chứ 

Cạnh của hình vuông là:

`35:4=8,75(cm)`

Diện tích hình vuông đó là:

`8,75 xx 8,75 = 76,5625 (cm^2)` 

ĐS: ... 

\(\left(3x-3\right)^2+\left(4y+2\right)^2=0\)

Ta có:

`(3x-3)^2>=0` với mọi x

`(4y+2)^2>=0` với mọi x

`=>(3x-3)^2+(4y+2)^2>=0` với mọi x,y

Mặt khác: `(3x-3)^2+(4y+2)^2=0`

Dấu "=" xảy ra: `3x-3=0` và `4y+2=0`

`=>3x=3` và `4y=-2`

`=>x=3/3=1` và `y=-2/4=-1/2` 

\(VT=\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\cdot\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\\ =\left[1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\cdot\left[1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right]\\ =\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\\ =1-\left(\sqrt{a}\right)^2\\ =1-a=VP\)