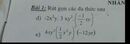Tìm số nguyên dương n nhỏ nhất sao cho 1000 ≤n ≤1100 và 1111 ^ n + 1222 ^ n + 1333 ^ n + 1444 ^ n chia hết cho 10.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(x^2+x-2=0\)
\(\Leftrightarrow x^2+2x-x-2=0\)
\(\Leftrightarrow\left(x-1\right).\left(x+2\right)=0\)
tới đây chắc bạn giải tiếp đc r

Bài 1 :
a, \(-2x^2y.3xy^2\left(-\frac{1}{2}xy\right)=3x^4y^4\)
b, \(4xy^2\left(\frac{1}{2}x^2y\right)^2\left(-12yz\right)=4xy^2.\frac{1}{4}x^4y^2\left(-12yz\right)=-12x^5y^5z\)

a) \(-x-y^2+x^2-y=-x-y+x^2-y^2=-\left(x+y\right)+\left(x-y\right)\left(x+y\right)\)\(=\left(x+y\right)\left(x-y-1\right)\)
b) \(x\left(x+y\right)-5x-5y=x\left(x+y\right)-5\left(x+y\right)=\left(x+y\right)\left(x-5\right)\)
c) \(x^2-5x+5y-y^2=x^2-y^2+5y-5x=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)\)\(=\left(x-y\right)\left(x+y-5\right)\)
d) \(5x^3-5x^2y-10x^2+10xy=5x^2\left(x-y\right)-10x\left(x-y\right)\)\(=\left(x-y\right)\left(5x^2-10x\right)=\left(x-y\right)5x\left(x-2\right)\)
e) \(27x^3-8y^3=\left(3x\right)^3-\left(2y\right)^3=\left(3x-2y\right)\left(9x^2+6xy+4y^2\right)\)
f) \(x^6-y^6=\left(x^2\right)^3-\left(y^2\right)^3=\left(x-y\right)\left(x+y\right)\left(x^4+x^2y^2+y^4\right)\)


\(x\left(a-b\right)-\left(a-b\right)=x\left(a-b\right)-1\left(a-b\right)=\left(x-1\right)\left(a-b\right)\)

Vì m, n là số nguyên tố nên m, n > 0
7m+n=31 suy ra \(7m\le31\)và \(7m⋮7\)\(\Rightarrow7m\in\left\{14;21;28\right\}\)
\(\Rightarrow m\in\left\{2;3;4\right\}\)\(\Rightarrow n\in\left\{17;10;3\right\}\)
Ta loại trường hợp n=10 và m=4 đi vì 10 và 4 là hợp số khi đó chỉ còn cặp số \(\left(m;n\right)=\left(2;17\right)\)
Khi đó \(m^n+n^m=2^{17}+17^2=131072+289=131361\)