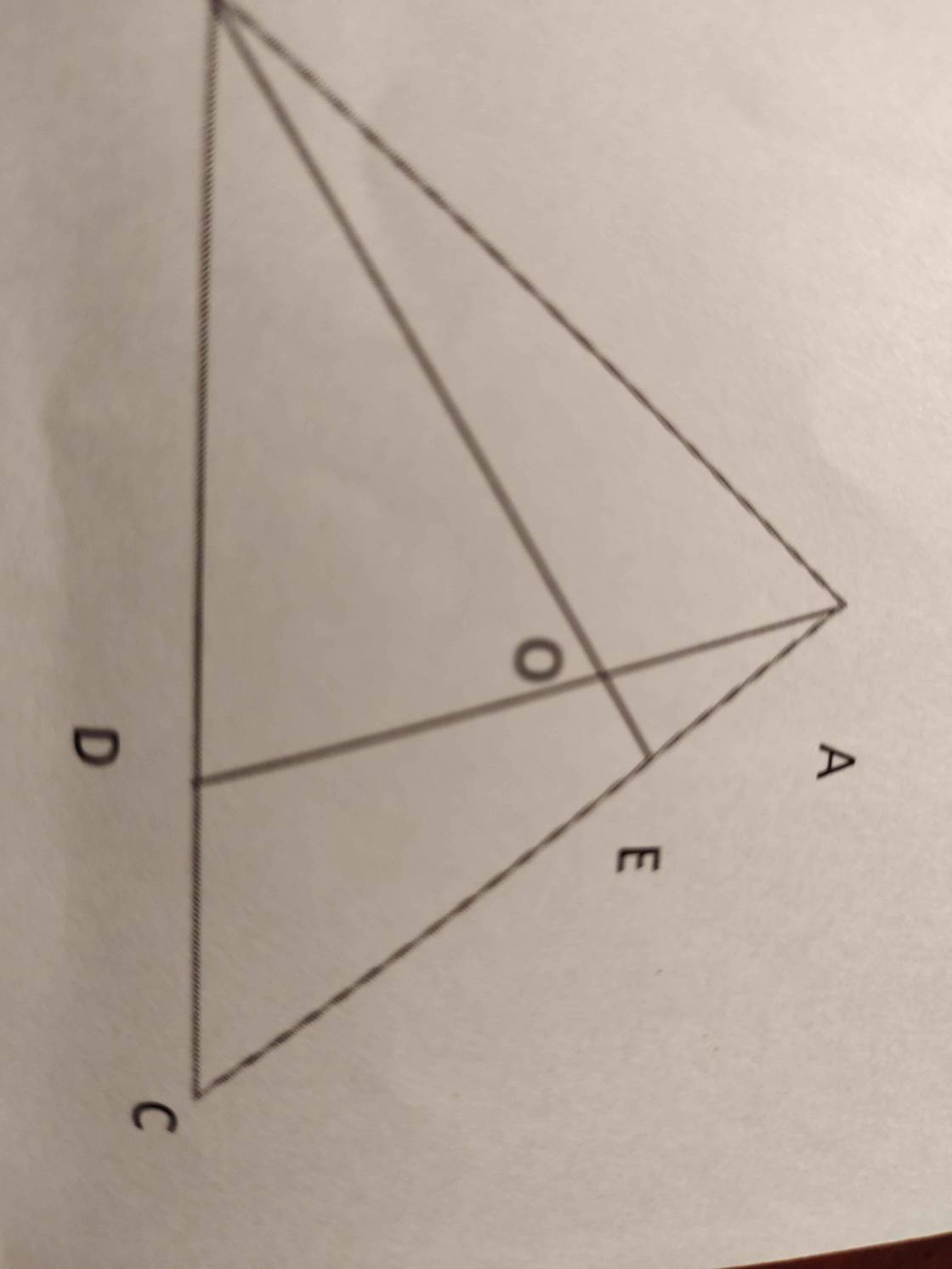
Cho tam giác abc trong đó CE = 2/3 ca CD = 1/3 CB
a, so sánh diện tích hai tam giác Abe và adc
b, so sánh đoạn BO với đoạn BE
c, tính diện tích tam giác AOE biết SABC là 210 cm vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Quy luật:
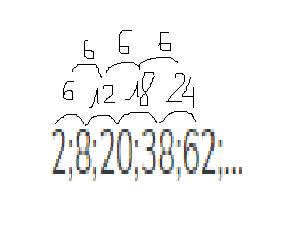
Khoảng cách giữa các khoảng cách của từng số hạng liên tiếp trong dãy số của đề bài là: 6.
b) Ta có dãy số từ khoảng cách của từng số hạng liên tiếp trong đề bài:
6; 12; 18; 24; ...
Khoảng cách giữa 2 số hạng liên tiếp: 6.
Số hạng thứ 49 của dãy mới sẽ được cộng với số hạng thứ 49 của dãy ban đầu (số thứ tự bị giảm do số lượng khoảng cách) = số hạng thứ 50 của dãy ban đầu.
Số hạng thứ 49 của dãy mới là:
6 + 6 x (49 - 1) = 294
Số số hạng của dãy là: 49
Số thứ 5 của dãy là:
2 + (294 + 6) x 49 : 2 = 7352

\(x-50\%\times x+60\%\times x=35+0,4\times x\\x-50\%\times x+60\% \times x=35+40\% \times x\\x\times 100\%-50\% \times x+60\% \times x-40\%\times x=35\\x\times(100\%-50\%+60\%-40\%)=35\\x\times(50\%+20\%)=35\\x\times70\%=35\\x=35:70\%\\x=50\)

gọi số hoa giấy của tổ l là x (bông)
theo đề bài thì số bông tổ ll nhiều hơn tổ l là 6 bông, nên số bông tổ ll là: x + 6 (bông)
gọi số hoa giấy tổ lll là y (bông)
số bông hoa cả lớp làm là:
x + (x + 6) + y (bông hoa)
đề bài cho biết số bông của cả lớp làm nhiều hơn so với số bông của tổ lll là 98 bông, nên ta có:
x + (x + 6) + y = y + 98 (bông)
x + x + 6 = 98
2x = 92
x = 46
số hoa giấy tổ ll là:
x + 6 = 46 + 6 = 52
vậy số bông tổ ll làm đc là 52 bông

\(\overline{ab,caa}+\overline{cb,aba}=\overline{bd,ba0}\)
\(\Rightarrow\overline{abcaa}+\overline{cbaba}=\overline{bdba0}\) (nhân 2 vế với 1000)
\(VP⋮10\Rightarrow VT⋮10\Rightarrow a=0\) hoặc \(a=5\)
Với \(a=0\)
\(\Rightarrow\overline{bc00}+\overline{cb0b0}=\overline{bdb00}\)
\(VP⋮100\Rightarrow VT⋮100\) mà \(\overline{bc00}⋮100\Rightarrow\overline{cb0b0}⋮100\Rightarrow b=0\)
\(\Rightarrow\overline{c00}+\overline{c0000}=\overline{d000}\) do VP là số có 4 chữ số nên trường hợp a=0 bị loại
Với \(a=5\)
\(\Rightarrow\overline{5bc55}+\overline{cb5b5}=\overline{bdb50}\)
\(\Rightarrow1000x\overline{5bc}+55+1000x\overline{cb5}+\overline{b5}=\overline{bdb50}\)
\(VP⋮25\Rightarrow VT⋮25\) mà \(1000x\overline{5bc}⋮25;1000x\overline{cb5}⋮25\Rightarrow55+\overline{b5}⋮25\)
\(55+\overline{b5}=55+10xb+5=10xb+50+10\)
\(50⋮25\Rightarrow10xb+10⋮25\Rightarrow b=4\) hoặc \(b=9\)
Với \(b=4\)
\(\Rightarrow\overline{54c55}+\overline{c4545}=\overline{4d450}\) Ta thấy \(\overline{54c55}>\overline{4d450}\)
=> b=4 loại
Với \(b=9\)
\(\Rightarrow\overline{59c55}+\overline{c9595}=\overline{9d950}\)
\(\Rightarrow59055+100xc+10000xc+9595=90950+1000xd\)
\(10100xc=22300+1000xd\)
\(101xc=223+10xd\)
\(\Rightarrow\overline{c0c}-223=10xd\)
\(10xd⋮10\Rightarrow\overline{c0c}-223⋮10\Rightarrow c=3\)
\(\Rightarrow101xc-223=101x3-223=80=10xd\Rightarrow d=8\)
Thử
59355+39595=98950 Thỏa mãn đề bài
Kết luận: a=5; b=9; c=3; d=8


27 x 37 + 27 x 63
= 27 x (37 + 63)
= 27 x 100
= 2700
