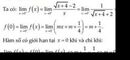Ta có limx→0−f(x)=limx→0−(mx+m+14)=m+14limx→0−⁡f(x)=limx→0−⁡(mx+m+14)=m+14.

limx→0+f(x)=limx→0+√x+4−2x=limx→0+x+4−4x(√x+4+2)=limx→0+1√x+4+2=14limx→0+⁡f(x)=limx→0+⁡x+4−2x=limx→0+⁡x+4−4x(x+4+2)=limx→0+⁡1x+4+2=14.

Để hàm số có giới hạn tạix=0x=0 thì limx→0−f(x)=limx→0+f(x)⇔m+14=14⇔m=0limx→0−⁡f(x)=limx→0+⁡f(x)⇔m+14=14⇔m=0.

em gửi bài

\(\hept{\begin{cases}lim_{x\rightarrow3^+}\frac{\left|x-3\right|}{x-3}=lim_{x\rightarrow3^+}\frac{x-3}{x-3}=1\\lim_{x\rightarrow3^-}\frac{\left|x-3\right|}{x-3}=lim_{x\rightarrow3^-}\frac{-x+3}{x-3}=-1\end{cases}\Rightarrow lim_{x\rightarrow3^+}\frac{\left|x-3\right|}{x-3}\ne lim_{x\rightarrow3^-}\frac{\left|x-3\right|}{x-3}}\)

=> đpcm

0

Đặt f(x)=cosx.

Chọn hai dãy số {xn} và {yn} với :

* xn=2nπ⇒xn→+∞ khi n→+∞ và ta được :

f(xn)=cos(xn)=cos(2nπ)=n→+∞1 .

* yn=π2+nπ⇒yn→+∞ khi n→+∞ và ta được :

f(yn)=cos(yn)=cos(π2+nπ)=n→+∞0.

Vậy limx→∞cosx không tồn tại.

Hai câu kia của mình bị lỗi ,không biết câu này có bị không

Đặt f(x)=cosx.

Chọn hai dãy số {xn} và {yn} với :

* xn=2nπ⇒xn→+∞ khi n→+∞ và ta được :

f(xn)=cos(xn)=cos(2nπ)=n→+∞1 .

* yn=π2+nπ⇒yn→+∞ khi n→+∞ và ta được :

f(yn)=cos(yn)=cos(π2+nπ)=n→+∞0.

Vậy limx→∞cosx không tồn tại.

Hai câu kia mình bị lỗi nha.

Với mọi dãy (x_n):x_n>1

\(\forall\)n và \(limx_n=1\)ta có \(lim_{x\rightarrow1^+}\frac{4x-3}{x-1}=lim\frac{4x_n-3}{x_n-1}=+\infty\)