 Mọi người giúp mk nhanh bài này với đc ko ạ mk đang cần gấp ai làm mk tick cho ạ
Mọi người giúp mk nhanh bài này với đc ko ạ mk đang cần gấp ai làm mk tick cho ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho tam giác ABC vuông tại A. Vẽ đường cao AH.Biết AB=3cm,AC =4cm
a)tính BC
b) tính HB,HC
c) tính AH

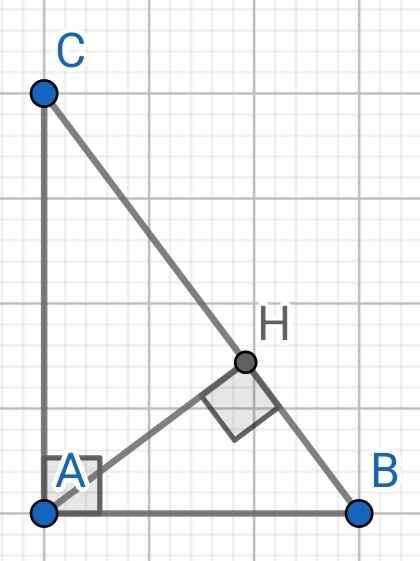
a) ∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pythagore)
= 3² + 4²
= 25
⇒ BC = 5 (cm)
b) Xét hai tam giác vuông: ∆ABC và ∆HBA có:
∠A chung
⇒ ∆ABC ∽ ∆HBA (g-g)
⇒ AB/HB = BC/AB
⇒ HB = AB²/BC
= 3²/5
= 1,8 (cm)
⇒ HC = BC - HB
= 5 - 1,8
= 3,2 (cm)
c) Do ∆ABC ∽ ∆HBA (cmt)
⇒ AC/AH = BC/AB
⇒ AH = AB.AC/BC
= 3.4/5
= 2,4 (cm)

Vận tốc của ô tô là:
\(\dfrac{205}{2,5}=82\) (km/h)
Vận tốc của xe máy là:
82 - 10 = 72 (km/h)
Vì vận tốc tối đa cho phép của ô tô là 50 km/h và của xe máy là 40 km/h, cả hai xe đều vi phạm luật giao thông vì đi quá tốc độ cho phép. Vì vậy, cả ô tô và xe máy đều bị phạt.

a) Tam giác ABC vuông tại A, AH là đường cao nên ta có:
∠BAH = ∠BAC và ∠ABH = ∠ABC (do cùng vuông góc với đường thẳng đứng)
Vậy tam giác HBA đồng dạng tam giác ABC theo qui tắc góc - góc.
Do đồng dạng nên ta có:
\(\dfrac{AB}{BH}=\dfrac{BH}{BC}\)
Từ đó suy ra:
AB2 = BH \(\cdot\) BC
b) M, N lần lượt là trung điểm của AB và AC nên AM = MB = \(\dfrac{1}{2}AB\) và AN = CN = \(\dfrac{1}{2}AC\).
Do tam giác ABC vuông cân tại A nên AB = AC, suy ra MB = NC. Vậy BMNC là hình thang cân.
Do MN là trung tuyến của tam giác ABC nên MN = \(\dfrac{1}{2}BC\) = AH (vì ABC là tam giác vuông cân).
c) K là giao điểm của AH và CM. Do MN // BC và MN = AH nên ta có tứ giác AMKN là hình bình hành. Suy ra AK = MN = AH.
Vì vậy, BC = BM + MC = BA + AC = 2AB = 3AK.

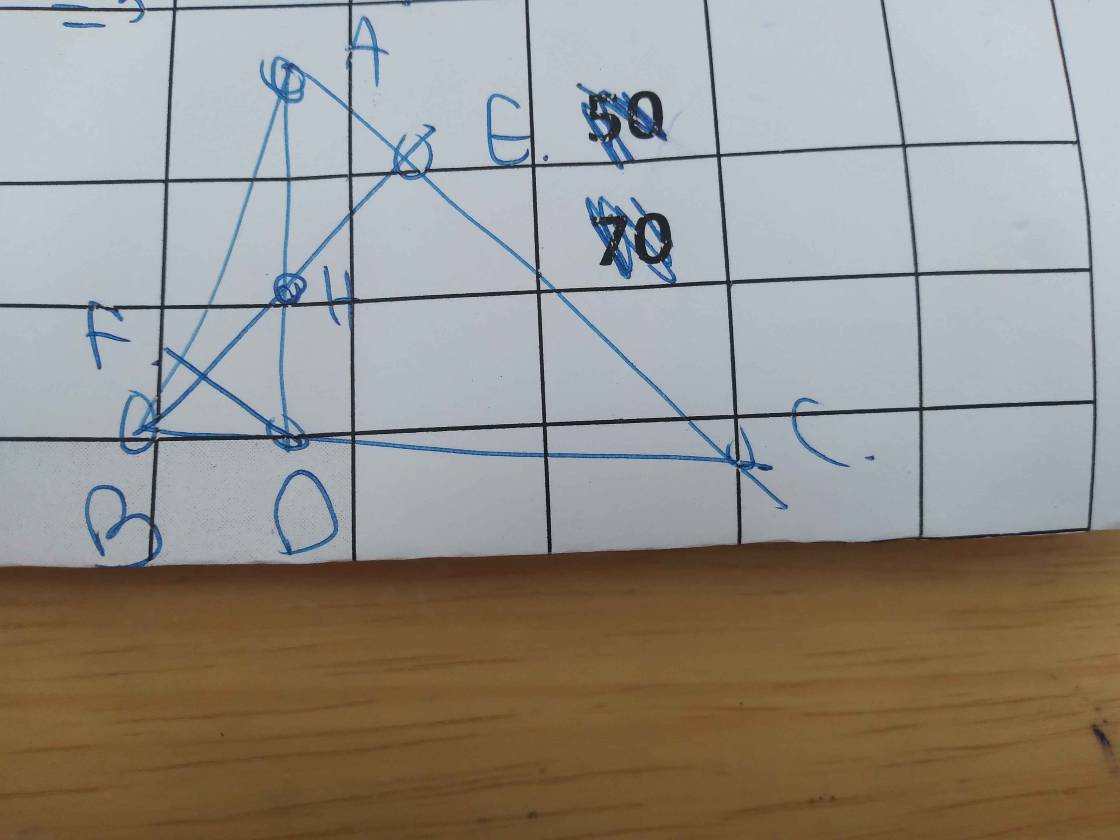
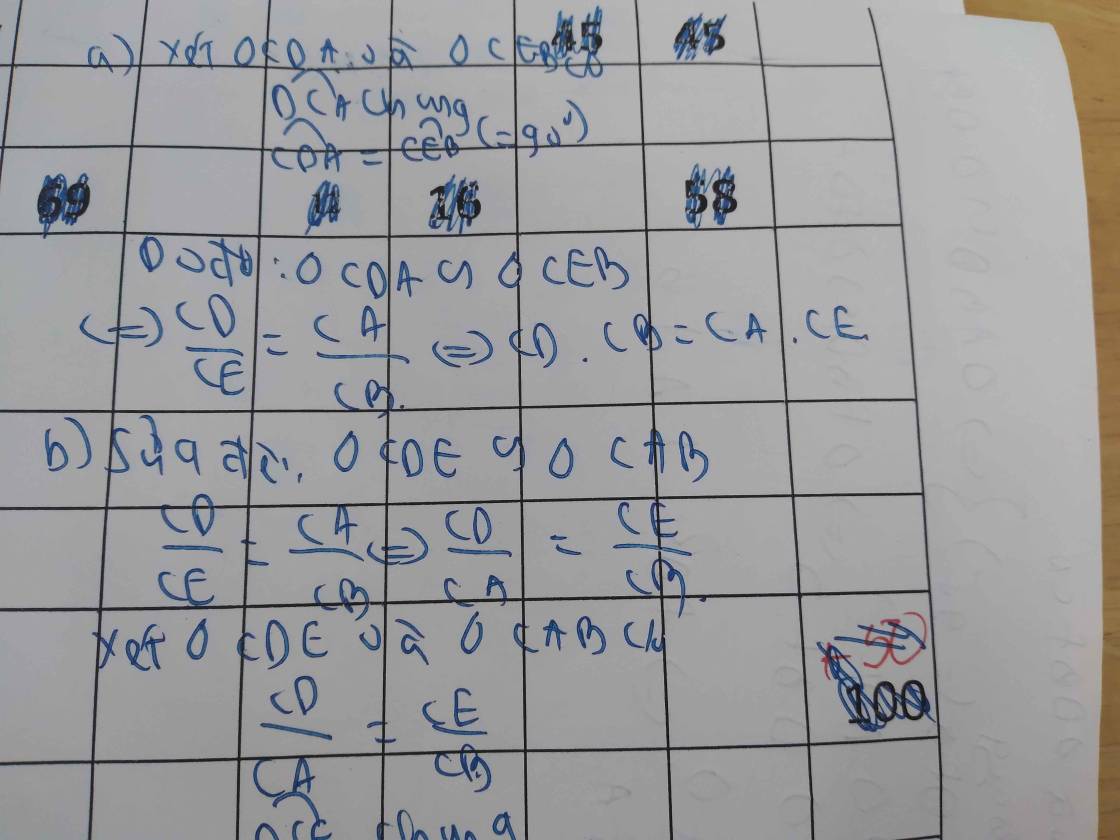
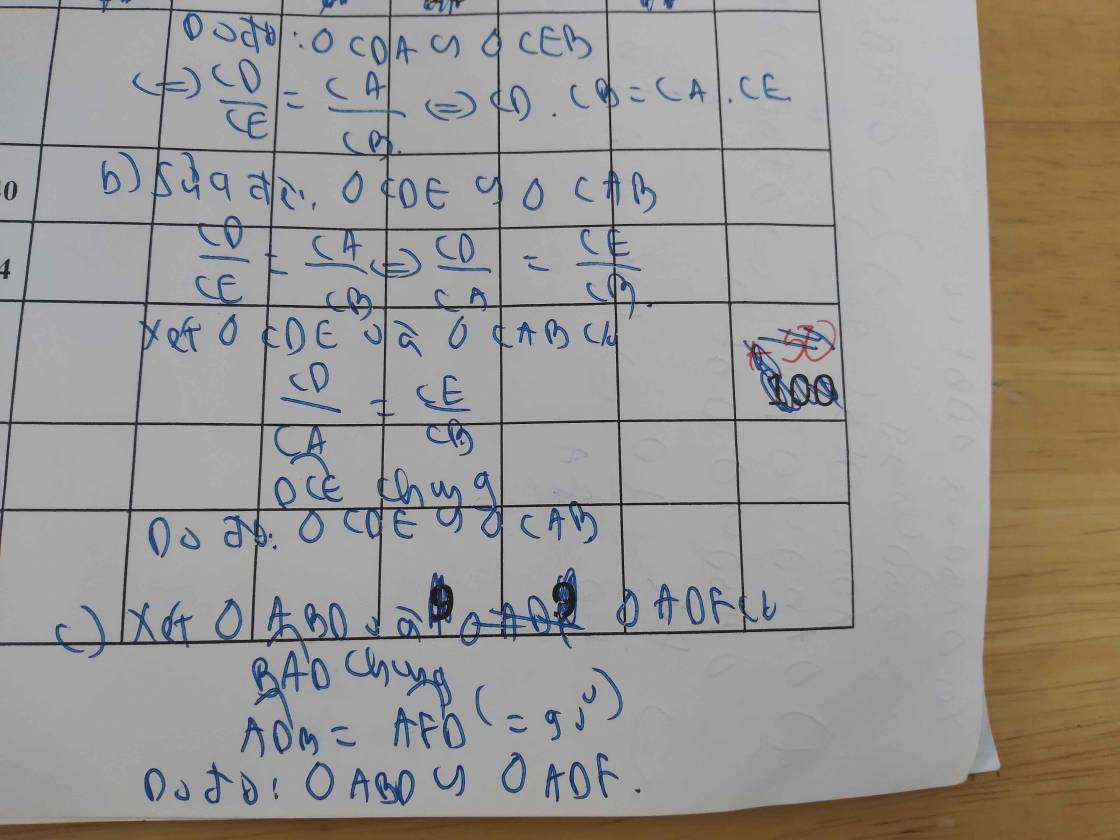


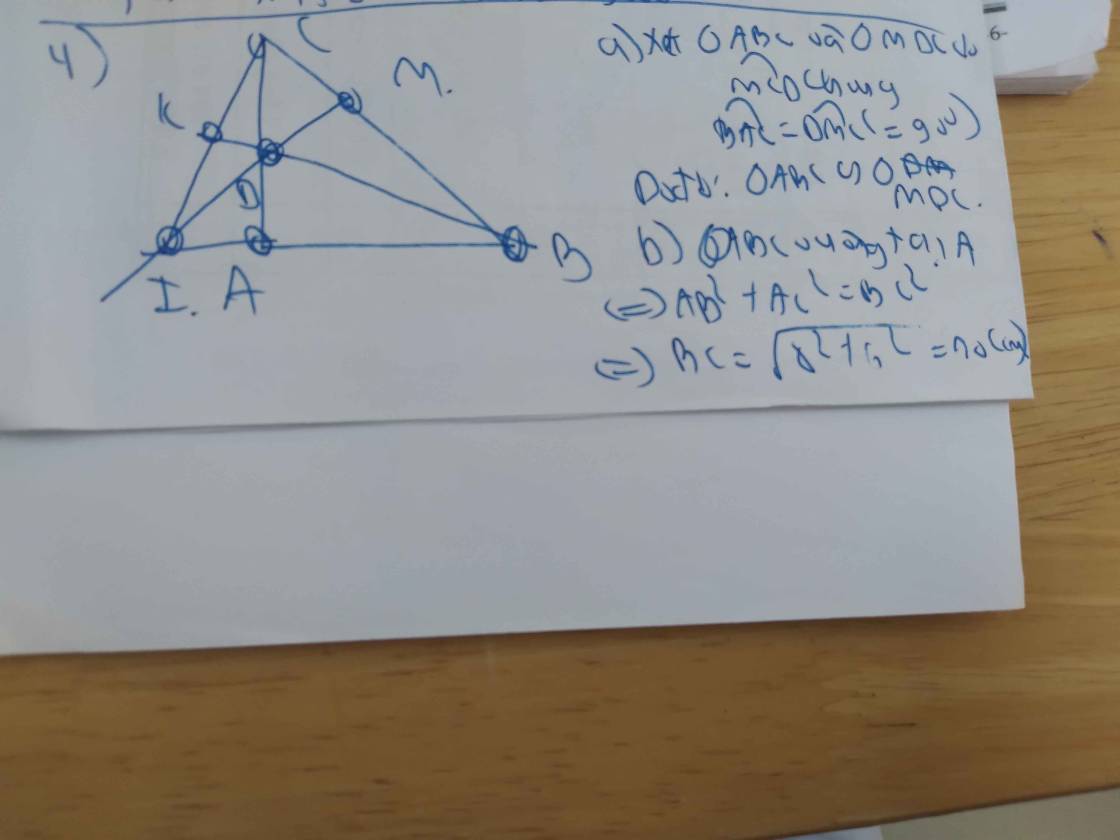
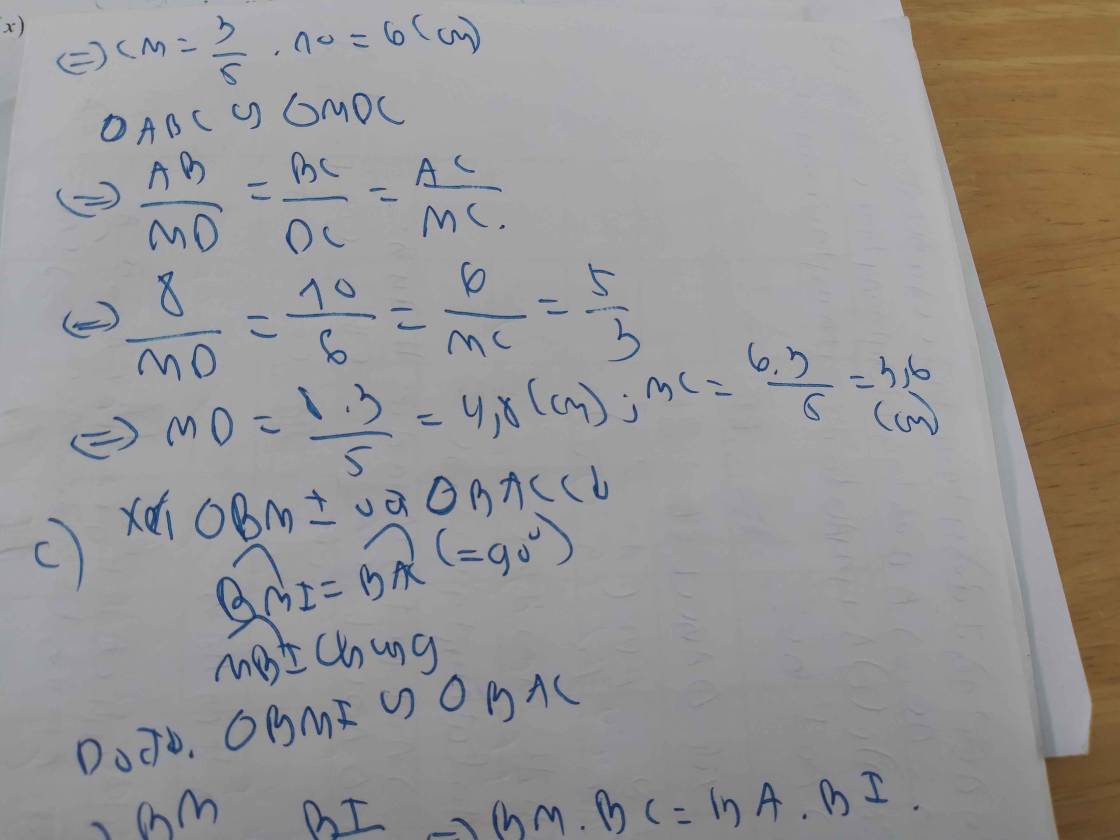


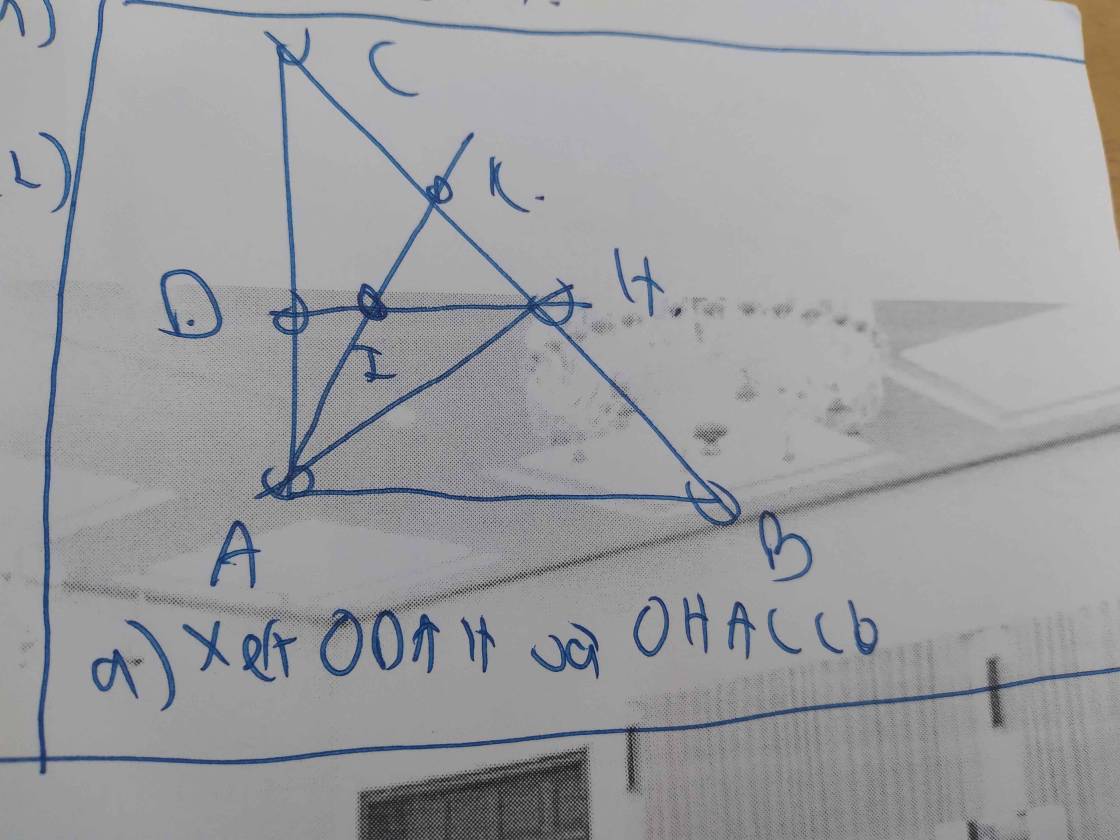



a) Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ ∠ADB = ∠CBD (so le trong)
⇒ ∠ADH = ∠CBK
Do ABCD là hình bình hành (gt)
⇒ AD = BC
Xét hai tam giác vuông: ∆ADH và ∆CBK có:
AD = BC (cmt)
∠ADH = ∠CBK (cmt)
⇒ ∆ADH = ∆CBK (cạnh huyền - góc nhọn)
⇒ AH = CK (hai cạnh tương ứng)
Do AH ⊥ BD (gt)
CK ⊥ BD (gt)
⇒ AH // CK
Tứ giác AHCK có:
AH // CK (cmt)
AH = CK (cmt)
⇒ AHCK là hình bình hành
b) Do AHCK là hình bình hành (cmt)
O là trung điểm của HK (gt)
⇒ O là trung điểm của AC
⇒ A, O, C thẳng hàng