Nó chỉ là cái tên (giống như đặt tên tam giác là ABC, MNP gì đó tùy thích).

Góc alpha có số đo bất kì và góc beta sẽ có số đo bất kì nhưng khác với góc alpha.

Lời giải:

Gọi $I$ là trung điểm $BC$

$\Rightarrow BI=IC=\frac{BC}{2}$

Tam giác $BEC$ vuông tại $E$ nên trung tuyến $EI=\frac{BC}{2}$
Tam giác $BDC$ vuông tại $D$ nên trung tuyến $DI=\frac{BC}{2}$

$\Rightarrow BI=IC=EI=DI=\frac{BC}{2}$ nên $I$ là tâm đường tròn đi qua $B,C,D,E$. Bán kính đường tròn đi qua $B,C,E,D$ là $\frac{BC}{2}$

Đáp án D.

Hình vẽ:

Hệ thức nào em nhỉ?

Nếu \(\Delta>0\) thì có 2 nghiệm phân biệt
Nếu\(\Delta< 0\) thì vô nghiệm
Nếu\(\Delta=0\) Thì \(x_1=x_2\)
Này đơn giản dễ nhớ mà=))

 Δ≥0 thì phương trình có 2 nghiệm

a) Ta có \(M\left(1,m\right)\) và \(N\left(-3,n\right)\).

Vì \(M,N\in\left(P\right):y=\dfrac{1}{2}x^2\) nên ta suy ra \(m=\dfrac{1}{2};n=\dfrac{9}{2}\)

Gọi đường thẳng cần tìm là \(d:y=ax+b\). Vì \(d\) đi qua M và N nên ta có hệ pt sau:

 \(\left\{{}\begin{matrix}\dfrac{1}{2}=a+b\\\dfrac{9}{2}=-3a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=\dfrac{3}{2}\end{matrix}\right.\).

Vậy ptđt cần tìm là \(d:y=-x+\dfrac{3}{2}\)

b) Mình chưa hiểu đề bài lắm. Thế nào là "cắt parabol tại 2 điểm đạt GTNN"?

có hình ko cho xin với

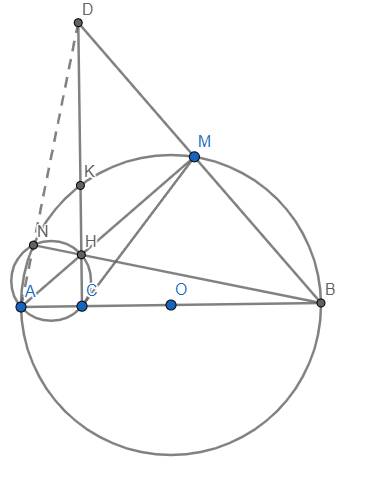
a) Xét đường tròn (O) có đường kính AB \(\Rightarrow\widehat{AMB}=90^o\)

\(\Rightarrow\widehat{AMD}=90^o\)

Lại có \(\widehat{ACD}=90^o\) nên tứ giác ACMD nội tiếp đường tròn (AD).

b) Tứ giác ACMD nội tiếp \(\Rightarrow\widehat{CAM}=\widehat{CDM}\) hay \(\widehat{CAH}=\widehat{DCB}\)

Từ đó dễ dàng chứng minh \(\Delta CAH~\Delta CDB\left(g.g\right)\)

\(\Rightarrow\dfrac{CA}{CD}=\dfrac{CH}{CB}\) \(\Rightarrow CA.CB=CH.CD\)

c) Ta thấy \(\widehat{ANH}=\widehat{ACH}=90^o\) nên tứ giác ANHC nội tiếp.

 Đồng thời \(\widehat{HMB}=\widehat{HCB}=90^o\) nên tứ giác HCBM nội tiếp.

 \(\Rightarrow\widehat{HCM}=\widehat{HBM}\).

 Từ đó dễ dàng suy ra \(\Delta DMC~\Delta DHB\left(g.g\right)\)

 \(\Rightarrow\dfrac{DM}{DH}=\dfrac{DC}{DB}\)

\(\Rightarrow DM.DB=DH.DC\)

\(\Rightarrow P_{D/\left(ANHC\right)}=P_{D/\left(O\right)}\)

\(\Rightarrow\) D thuộc trục đẳng phương của (ANHC) và (O)

\(\Rightarrow A,N,D\) thẳng hàng.

Gọi chiều dài lúc đầu là \(x\) (m); \(x>0\)

Thì chiều rộng lúc đầu là: 160: 2 - \(x\) = 80 - \(x\) 

Chiều rộng lúc sau là: (100% + 20%).(80- \(x\)) = 1,2.(80 - \(x\)) 

Chiều dài lúc sau là: (100%- 10%).\(x\)           = 0,9\(x\)

Theo bài ra ta có phương trình:

         \(\dfrac{1,2.\left(80-x\right)}{0,9x}\) = \(\dfrac{4}{5}\)  

         5.1,2.(80 - \(x\))  = 4.0,9\(x\)

                480 - 6\(x\) = 3,6\(x\)

                6\(x\) + 3,6\(x\) = 480

                   9,6\(x\)      = 480

                        \(x\)      = 480 : 9,6

                        \(x\)      = 50

Chiều rộng là 80 - 50 = 30 (m)

Diện tích hình chữ nhật lúc đầu là: 50 x 30 = 1500 (m²)

Kết luận: Diện tích hình chữ nhật lúc đầu là: 1500 m²