Một khu vườn hình chữ nhật có chu vi là 450 m. Nếu giảm chiều dài đi 1/5 chiều dài cũ và tăng chiều rộng thêm 1/4 chiều rộng cũ thì chu vi của khu vườn không thay đổi. Tìm chiều dài và chiều rộng của khu vườn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi 10p=1/6(giờ)
Sau 1/6 giờ thì xe máy đi được \(40\cdot\dfrac{1}{6}=\dfrac{20}{3}\left(km\right)\)
Độ dài quãng đường còn lại là \(120-\dfrac{20}{3}=\dfrac{340}{3}\left(km\right)\)
Tổng vận tốc hai xe là 60+40=100(km/h)
Hai xe gặp nhau sau khi xe ô tô đi được:
\(\dfrac{340}{3}:100=\dfrac{340}{300}=\dfrac{17}{15}\left(giờ\right)\)

3 giờ 20 phút = 10/3 giờ
Gọi x (km/h) là vận tốc của tàu thủy khi nước yên lặng (x > 4)
Vận tốc khi xuôi dòng của tàu thủy là: x + 4 (km/h)
Vận tốc ngược dòng của tàu thủy: x - 4 (km/h)
Quãng đường đi xuôi dòng: (x + 4).10/3 (km)
Quãng đường đi ngược dòng: (x - 4).5 (km)
Theo đề bài, ta có phương trình:
(x + 4).10/3 = (x - 4).5
(x + 4).10 = (x - 4).15
10x + 40 = 15x - 60
10x - 15x = -60 - 40
-5x = -100
x = -100 : (-5)
x = 20 (nhận)
Vậy vận tốc của tàu thủy khi nước yên lặng là 20 km/h
Giải toán bằng cách lập phương trình em nhé.
Giải:
Gọi vân tốc của ca nô khi nước lặng là \(x\) (km/h) ; \(x>0\)
Vận tốc ca nô xuôi dòng là: \(x+4\) (km/h)
Đổi 3 giờ 20 phút = \(\dfrac{10}{3}\) giờ
Quãng sông AB là: (\(x+4\)) x \(\dfrac{10}{3}\) (km)
Vận tốc ca nô khi ngược dòng là: \(x\) - 4 (km)
Quãng sông AB là: (\(x-4\)) x 5 (km)
Theo bài ra ta có phương trình:
(\(x+4\)) x \(\dfrac{10}{3}\) = (\(x-4\)) x 5
(\(x+4\)) x 10 = (5\(x\) - 20) x 3
10\(x\) + 40 = 15\(x\) - 60
15\(x\) - 10\(x\) = 40 + 60
5\(x\) = 100
\(x\) = 100 : 5
\(x\) = 20
Vậy vận tốc ca nô khi nước lặng là: 20 km/h

Bài 8
Gọi x (đồng) là giá tiền sản phẩm loại I (0 < x < 110000)
Giá sản phẩm loại II là: 120000 - 10000 - x = 110000 - x (đồng)
Giá sản phẩm loại I sau khi có VAT: x + 100%x = 1,1x (đồng)
Giá sản phẩm loại II sau khi có VAT:
110000 - x + 0,08(110000 - x) (đồng)
Theo đề bài ta có phương trình:
1,1x + 110000 - x + 0,08(110000 - x) = 120000
0,1x + 110000 + 8800 - 0,08x = 120000
0,02x = 120000 - 110000 - 8800
0,02x = 1200
x = 1200 : 0,02
x = 60000 (nhận)
Vậy nếu không kể VAT thì phải trả sản phẩm loại I giá 60000 đồng, loại II giá 110000 - 60000 = 50000 đồng
Bài 7
Giá chiếc áo len sau khi giảm so với giá ban đầu là:
100% - 30% = 70%
Giá chiếc áo len ban đầu là:
399000 : 70% = 570000 (đồng)

Bài 6:
Gọi số áo được giao là x(cái)
(Điều kiện: \(x\in Z^+\))
Số cái áo thực tế may được là x+8(cái)
Thời gian thực tế hoàn thành công việc là:
25-1=24(ngày)
Số cái áo dự định may trong mỗi ngày là \(\dfrac{x}{25}\left(cái\right)\)
Số cái áo thực tế may được trong mỗi ngày là \(\dfrac{x+8}{24}\left(cái\right)\)
Thực tế trong mỗi ngày may được nhiều hơn dự định 2 cái nên ta có:
\(\dfrac{x+8}{24}-\dfrac{x}{25}=2\)
=>\(\dfrac{25\left(x+8\right)-24x}{600}=2\)
=>x+200=1200
=>x=1000(nhận)
vậy: Số ao được giao là 1000 cái
Bài 7:
Giá ban đầu của áo len là:
\(399000:\left(1-30\%\right)=570000\left(đồng\right)\)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{FAE}\) chung
Do đó: ΔAEF~ΔABC
b:
Gọi giao điểm của AD,BE,CF là H
Xét tứ giác AFHE có \(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
nên AFHE là tứ giác nội tiếp
Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BFHD là tứ giác nội tiếp
Ta có: \(\widehat{HFE}=\widehat{HAE}\)(AFHE nội tiếp)
\(\widehat{HFD}=\widehat{HBD}\)(BFHD nội tiếp)
mà \(\widehat{HAE}=\widehat{HBD}\left(=90^0-\widehat{ACB}\right)\)
nên \(\widehat{HFE}=\widehat{HFD}\)
=>\(\widehat{CFE}=\widehat{CFD}\)
=>FC là phân giác của góc EFD

a: Xét ΔIAB và ΔIMD có
\(\widehat{IAB}=\widehat{IMD}\)(hai góc so le trong, AB//MD)
\(\widehat{AIB}=\widehat{MID}\)(hai góc đối đỉnh)
Do đó: ΔIAB~ΔIMD
=>\(\dfrac{IA}{IM}=\dfrac{IB}{ID}=\dfrac{AB}{MD}=\dfrac{AB}{MC}\left(1\right)\)
Xét ΔKAB và ΔKCM có
\(\widehat{KAB}=\widehat{KCM}\)(hai góc so le trong, AB//CM)
\(\widehat{AKB}=\widehat{CKM}\)(hai góc đối đỉnh)
Do đó: ΔKAB~ΔKCM
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KM}=\dfrac{AB}{CM}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{KA}{KC}=\dfrac{KB}{KM}=\dfrac{IA}{IM}=\dfrac{IB}{ID}\)
=>\(\dfrac{MI}{IA}=\dfrac{MK}{KB}\)
Xét ΔMAB có \(\dfrac{MI}{IA}=\dfrac{MK}{KB}\)
nên IK//AB
Ta có: IK//AB
AB//CD
Do đó: IK//CD
b: Xét ΔMAB có IK//AB
nên \(\dfrac{IK}{AB}=\dfrac{MI}{MA}\)
=>\(\dfrac{AB}{IK}=\dfrac{MA}{MI}=1+\dfrac{IA}{IM}=1+\dfrac{AB}{MD}\)
=>\(\dfrac{AB}{IK}=1+\dfrac{AB}{\dfrac{CD}{2}}\)
=>\(\dfrac{AB}{IK}=1+\dfrac{2AB}{CD}\)
=>\(AB\left(\dfrac{1}{IK}-\dfrac{2}{CD}\right)=1\)
=>\(\dfrac{1}{IK}-\dfrac{2}{CD}=\dfrac{1}{AB}\)
=>\(\dfrac{1}{AB}+\dfrac{2}{CD}=\dfrac{1}{IK}\)

\(\left(2x^2-3\right)^2-16\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(2x^2-3\right)^2-\left[4\left(x+3\right)\right]^2=0\)
\(\Leftrightarrow\left[\left(2x^2-3\right)-4\left(x+3\right)\right]\left[\left(2x^2-3\right)+4\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(2x^2-4x-15\right)\left(2x^2+3x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x^2-4x-15=0\\2x^2+3x+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2\left(x^2-2x\right)-15=0\\2\left(x^2+\dfrac{3}{2}x\right)+9=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2\left(x^2-2x+1\right)-2-15=0\\2\left[x^2+2\cdot x\cdot\dfrac{3}{4}+\left(\dfrac{3}{4}\right)^2\right]-2\cdot\left(\dfrac{3}{4}\right)^2+9=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2\left(x-1\right)^2=17\\2\left(x+\dfrac{3}{4}\right)^2+\dfrac{63}{8}=0\left(\text{vô lí}\right)\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)^2=\dfrac{17}{2}\Leftrightarrow\left[{}\begin{matrix}x-1=\dfrac{\sqrt{34}}{2}\\x-1=-\dfrac{\sqrt{34}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2+\sqrt{34}}{2}\\x=\dfrac{2-\sqrt{34}}{2}\end{matrix}\right.\)
Vậy pt đã cho có nghiệm là: \(x\in\left\{\dfrac{2+\sqrt{34}}{2};\dfrac{2-\sqrt{34}}{2}\right\}\).



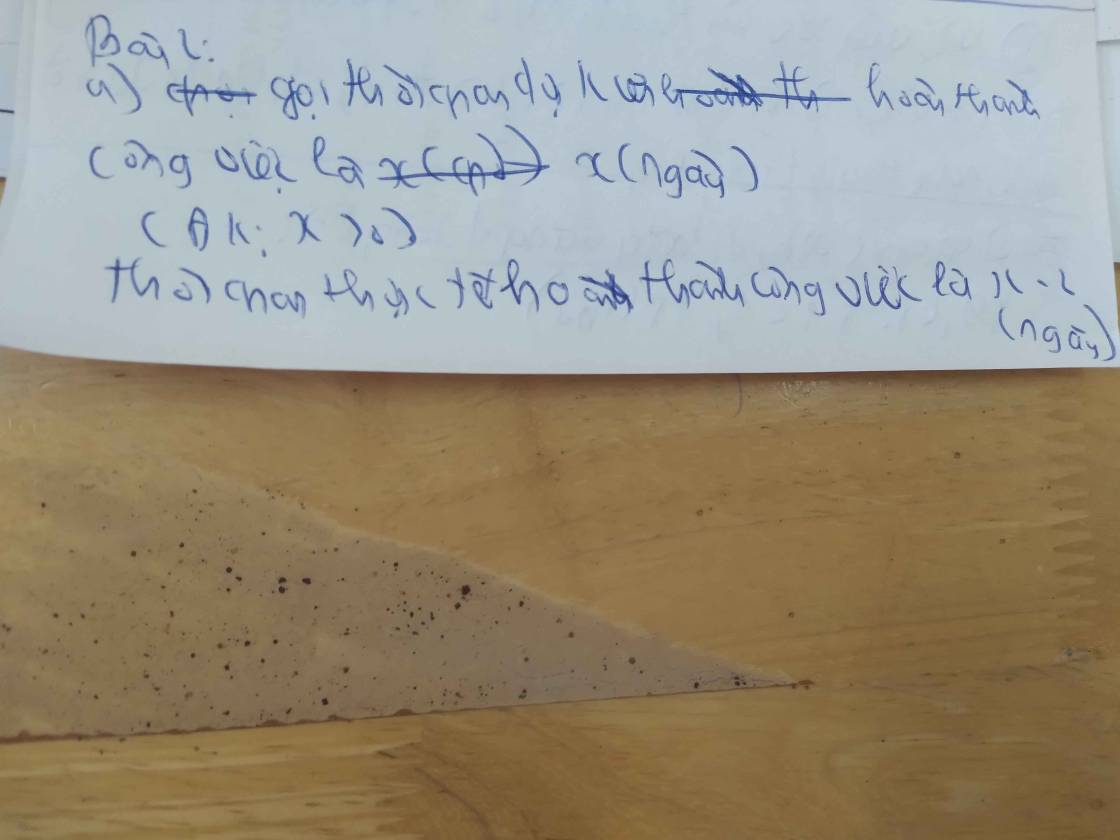



Nửa chu vi khu vườn là 450:2=225(m)
Gọi chiều dài khu vườn là x(m)
(ĐK: \(x>\dfrac{225}{2}=112,5\))
Chiều rộng khu vườn là 225-x(m)
Chiều dài khu vườn lúc sau là \(x\left(1-\dfrac{1}{5}\right)=\dfrac{4}{5}x\left(m\right)\)
Chiều rộng khu vườn lúc sau là \(\left(225-x\right)\cdot\left(1+\dfrac{1}{4}\right)=\dfrac{5}{4}\left(225-x\right)\left(m\right)\)
Chu vi không đổi nên ta có phương trình:
\(\dfrac{4}{5}x+\dfrac{5}{4}\left(225-x\right)=225\)
=>\(\dfrac{4}{5}x+\dfrac{1125}{4}-\dfrac{5}{4}x=225\)
=>\(\dfrac{-9}{20}x=225-\dfrac{1125}{4}\)
=>\(\dfrac{-9}{20}x=-56,25\)
=>x=125(nhận)
Chiều rộng khu vườn là 225-125=100(m)
Vậy: Chiều dài là 125m; chiều rộng là 100m
1\6>5\9