a: Độ dài quãng đường ô tô đi được sau t giờ là:

\(S=60t\left(km\right)\)

b: Thời gian ô tô đi từ Đà Nẵng đến Quảng Ngãi là:

150:60=2,5(giờ)=2h30p

Ô tô đến nơi lúc:

7h+2h30p=9h30p

2x=3y

=>\(\dfrac{x}{3}=\dfrac{y}{2};\dfrac{x}{y}=\dfrac{3}{2};\dfrac{3}{x}=\dfrac{2}{y};\dfrac{y}{x}=\dfrac{2}{3}\)

a: Xét ΔABC có AB<AC<BC

mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC

nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)

b: Sửa đề: A là trung điểm của BD, DK cắt CA tại N

Xét ΔCDB có

CA,DK là các đường trung tuyến

CA cắt DK tại M

Do đó: M là trọng tâm của ΔCDB

=>\(CM=\dfrac{2}{3}CA=\dfrac{2}{3}\cdot12=8\left(cm\right)\)

c: Sửa đề; Chứng minh B,M,Q thẳng hàng

Gọi I là trung điểm của CA

Đường trung trực của AC cắt CD tại Q 

mà I là trung điểm của AC

nên QI\(\perp\)AC và I là trung điểm của aC

=>QI//DA

Xét ΔCAD có

I là trung điểm của CA

IQ//DA

Do đó: Q là trung điểm của CD

Xét ΔCDB có

M là trọng tâm

Q là trung điểm của CD

Do đó: B,M,Q thẳng hàng

A. 12 nha

 Đây là dạng toán nâng cao chuyên đề dãy só có quy luật, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng xét dãy số phụ như sau:

                    Giải:

Cho dãy số: 2; 14; 6; 18; 10; 22;...(1)

Các số ở vị trí lẻ của dãy (1) là các số thuộc dãy số:

      2; 6; 10;...;

Đây là dãy số cách đều với khoảng cách là: 6 - 2 = 4

 Các số chẵn của dãy số (1) là các số thuộc dãy số:

       14; 18; 22;...

Dãy số trên là dãy số cách đều với khoảng cách là: 18 - 14 = 4

Vì số cần điền vào chỗ... của dãy (1) là số ở vị trí lẻ nên số cần điền vào chỗ... của dãy (1) là số thuộc dãy:

       2; 6; 10;...

Vậy đó là số: 10 + 4  = 14

Chọn b; 14 

Đề yêu cầu gì thế bạn?

DĐúm òi 

Thiếu j ko bn?

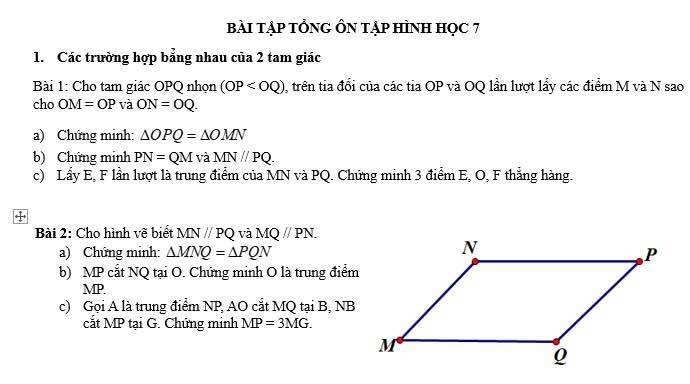
Bài 2:

a: Xét ΔMNQ và ΔPQN có

\(\widehat{MNQ}=\widehat{PQN}\)(MN//PQ)

NQ chung

\(\widehat{MQN}=\widehat{PNQ}\)(MQ//NP)

Do đó: ΔMNQ=ΔPQN

b:

ΔMNQ=ΔPQN

=>MQ=PN; MN=PQ

Xét ΔOMN và ΔOPQ có

\(\widehat{OMN}=\widehat{OPQ}\)(MN//PQ)

MN=PQ

\(\widehat{ONM}=\widehat{OQP}\)(MN//PQ)

Do đó: ΔOMN=ΔOPQ

=>OM=OP

=>O là trung điểm của MP

c: ΔOMN=ΔOPQ

=>ON=OQ

Xét ΔOAN và ΔOBQ có

\(\widehat{ONA}=\widehat{OQB}\)(NA//BQ)

ON=OQ

\(\widehat{AON}=\widehat{BOQ}\)(hai góc đối đỉnh)

Do đó: ΔOAN=ΔOBQ

=>AN=BQ

=>\(BQ=\dfrac{1}{2}MQ\)

=>B là trung điểm của MQ

Xét ΔMQN có

NB,MO là các đường trung tuyếm

NB cắt MO tại G

Do đó: G là trọng tâm của ΔMQN

=>\(MG=\dfrac{2}{3}MO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot MP=\dfrac{1}{3}MP\)

=>MP=3MG

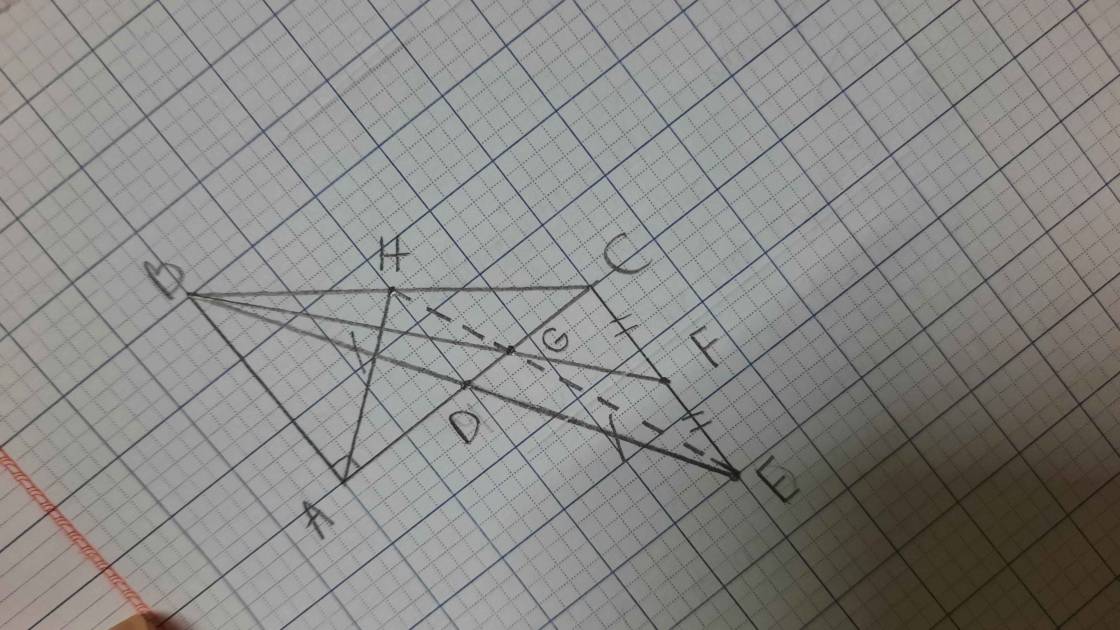
Bài 1:

a: Xét ΔOPQ và ΔOMN có

OP=OM

\(\widehat{POQ}=\widehat{MON}\)(hai góc đối đỉnh)

OQ=ON

Do đó: ΔOPQ=ΔOMN

b: ΔOPQ=ΔOMN

=>\(\widehat{OPQ}=\widehat{OMN}\)

=>PQ//MN

Xét ΔONP và ΔOQM có

ON=OQ

\(\widehat{NOP}=\widehat{QOM}\)(hai góc đối đỉnh)

OP=OM

Do đó: ΔONP=ΔOQM

=>NP=QM

c: ΔOMN=ΔOPQ

=>MN=PQ

mà \(NF=\dfrac{NM}{2};QE=\dfrac{QP}{2}\)

nên NF=QE

Xét ΔFNO và ΔEQO có

FN=EQ

\(\widehat{FNO}=\widehat{EQO}\)

NO=QO

Do đó: ΔFNO=ΔEQO

=>\(\widehat{FON}=\widehat{EOQ}\)

=>\(\widehat{FON}+\widehat{FOE}=180^0\)

=>N,O,E thẳng hàng

\(P\left(x\right)=\left(x-b\right)\left(x^2-5x+a\right)\)

Q(x)=x³+125

Để P(x)=Q(x) thì \(\left(x-b\right)\left(x^2-5x+a\right)=x^3+125\)

=>\(x^3-5x^2+a\cdot x-bx^2+5b\cdot x-ab=x^3+125\)

=>\(x^2\left(-b-5\right)+x\left(a+5b\right)-ab=125\)

=>\(\left\{{}\begin{matrix}-b-5=0\\a+5b=0\\-ab=125\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-5\\a=-5b=-5\cdot\left(-5\right)=25\\-25\cdot\left(-5\right)=125\left(đúng\right)\end{matrix}\right.\)

=>a=25 và b=-5

ai giải giúp mik vs

Câu 1: B

Câu 2: C

Câu 3: C

Câu 4: B

Câu 5: B

Câu 6: D

Câu 7: A

Câu 8: A

Câu 9: D

Câu 10: A