Cho đa thức \(P\left(x\right)=\dfrac{5x^3}{4}+\dfrac{5x^2}{6}-\dfrac{21x}{4}+\dfrac{1}{6}\). Tìm số dư khi chia \(P\left(x\right)\) cho \(2x-5\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
Xét tg vuông AMO có
\(\sin\widehat{AMO}=\dfrac{OA}{OM}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AMO}=30^o\)
Xét tg vuông AMO và tg vuông BMO có
MO chung; OA=OB=R => tg AMO = tg BMO (Hai tg vuông có cạnh huyền và 1 cạnh góc vuông bằng nhau)
\(\Rightarrow\widehat{AMO}=\widehat{BMO}=30^o\Rightarrow\widehat{AMO}+\widehat{BMO}=\widehat{AMB}=30^o+30^o=60^o\)
Xét tg MAB có
tg AMO = tg BMO (cmt) => MA=MB => tg MAB cân tại M
\(\Rightarrow\widehat{MAB}=\widehat{MBA}\)
Ta có
\(\widehat{MBA}+\widehat{MAB}=180^o-\widehat{AMB}=180^0-60^o=120^o\)
\(\Rightarrow2\widehat{MAB}=120^o\Rightarrow\widehat{MAB}=\widehat{MBA}=120^o:2=60^o\)
\(\Rightarrow\widehat{AMB}=\widehat{MAB}=\widehat{MBA}=60^o\) => tg MAB là tg đều
b/ Gọi H là giao của MO với AB
\(\Rightarrow AB\perp MO;HA=HB\) (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm vuông góc và chia đôi đoạn thẳng nối 2 tiếp điểm)
Ta có
\(S_{AOC}=\dfrac{1}{2}.HA.OC;S_{BOC}=\dfrac{1}{2}.HB.OC\) mà HA=HB (cmt)
\(\Rightarrow S_{AOC}=S_{BOC}\)
\(S_{AOBC}=S_{AOC}+S_{BOC}=2.S_{AOC}=HA.OC\)
Xét tg vuông AMO có
\(AO^2=OH.MO\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow OH=\dfrac{AO^2}{MO}=\dfrac{R^2}{2R}=\dfrac{R}{2}\)
Ta có
\(MH=MO-OH=2R-\dfrac{R}{2}=\dfrac{3R}{2}\)
Ta có
\(HA^2=MH.OH\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow HA=\sqrt{MH.OH}=\sqrt{\dfrac{3R}{2}.\dfrac{R}{2}}=\dfrac{R\sqrt{3}}{2}\)
\(\Rightarrow S_{AOBC}=HA.OC=\dfrac{R\sqrt{3}}{2}.R=\dfrac{R^2\sqrt{3}}{2}\)
c/
Ta có
\(MA\perp OA;OD\perp OA\) => MA//OD
\(\Rightarrow\widehat{MOD}=\widehat{AMO}=30^o\) (góc so le trong)
Xét tg vuông BMO có
\(\widehat{MOB}=90^o-\widehat{OMB}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{BOD}=\widehat{MOB}-\widehat{MOD}=60^o-30^o=30^o\)
\(\Rightarrow\widehat{MOD}=\widehat{BOD}=30^o\)
Xét tg BOD và tg COD có
\(OB=OC=R\)
OD chung
\(\widehat{BOD}=\widehat{MOD}\) (cmt)
=> tg BOD = tg COD (c.g.c)\(\Rightarrow\widehat{OCD}=\widehat{OBD}=90^o\Rightarrow CD\perp OC\)
=> CD là tiếp tuyến với (O)


\(\Leftrightarrow36x-20=4y^2-4y\)
\(\Leftrightarrow18\left(2x-1\right)=\left(2y-1\right)^2+1\)
Vế trái chia hết cho 3, vế phải chia 3 luôn dư 1 hoặc 2
Vậy không tồn tại cặp số nguyên x, y thỏa mãn
Vì \(9x-5\equiv4\left[9\right]\) nên \(y\left(y-1\right)=y^2-y\equiv4\left[9\right]\) hay \(y^2-y-4⋮9\)
\(\Leftrightarrow y^2-5y+4y-20+16⋮9\)
\(\Leftrightarrow\left(y-5\right)\left(y+4\right)+16⋮9\)
\(\Leftrightarrow\left(y-5\right)\left(y+4\right)-2⋮9\)
\(\Leftrightarrow\left(y-5\right)\left(y-5+9\right)-2⋮9\)
\(\Leftrightarrow\left(y-5\right)^2+9\left(y-5\right)-2⋮9\)
\(\Leftrightarrow\left(y-5\right)^2-2⋮9\)
\(\Rightarrow\left(y-5\right)^2-2⋮3\) hay \(\left(y-5\right)^2\equiv2\left(mod3\right)\)
Điều này là vô lí vì số chính phương khi chia cho 3 không thể có số dư là 2.
Vậy pt đã cho không có nghiệm nguyên.

\(5^{2009}=5^{2000}\cdot5^9\)
Ta có: \(5^{2000}\equiv1\) (\(mod\) \(10000\))
\(5^9\equiv3125\) (\(mod\) \(10000\))
\(\Rightarrow5^{2000}\cdot5^9\equiv1\cdot3125\) (\(mod\) \(10000\))
\(\Rightarrow5^{2009}\equiv3125\) (\(mod\) \(10000\))
Vậy \(4\) chữ số tận cùng của \(5^{2009}\) là \(3125\)

Đặt \(\left\{{}\begin{matrix}\sqrt[3]{x}=a\\\sqrt[3]{y}=b\end{matrix}\right.\) hệ trở thành \(\left\{{}\begin{matrix}2\left(a^3+b^3\right)=3\left(a^2b+ab^2\right)\\a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left[\left(a+b\right)^3-3ab\left(a+b\right)\right]=3ab\left(a+b\right)\\a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(6^3-18ab\right)=18ab\\a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}ab=8\\a+b=6\end{matrix}\right.\)
\(\Rightarrow\) a và b là nghiệm của \(t^2-6t+8=0\Rightarrow\left[{}\begin{matrix}t=4\\t=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=4;b=2\\a=2;b=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=64;y=8\\x=8;y=64\end{matrix}\right.\)

- Số lớn nhất \(\Rightarrow x=y=9\), khi đó nó có dạng: \(\overline{19293z}\) chia hết cho 7
\(\Rightarrow\overline{93z}-192\) chia hết cho 7
\(\Rightarrow930+z-192=738+z⋮7\)
\(\Rightarrow z+3⋮7\)
Mà z lớn nhất \(\Rightarrow z=4\)
Vậy số lớn nhất là \(192934\)
- Số nhỏ nhất \(\Rightarrow x=y=0\), khi đó có dạng \(\overline{10203z}\) chia hết cho 7
\(\Rightarrow102-\overline{3z}⋮7\Rightarrow102-\left(30+z\right)⋮7\)
\(\Rightarrow z-2⋮7\), mà z nhỏ nhất \(\Rightarrow z=2\)
Vậy số nhỏ nhất là \(102032\)
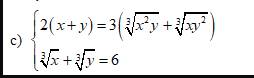
Lời giải:
Theo định lý Bê-du về phép chia đa thức, số dư của $P(x)$ khi chia $2x-5$ là $P(\frac{5}{2})=\frac{5}{4}(\frac{5}{2})^3+\frac{5}{6}(\frac{5}{2})^2-\frac{21}{4}.\frac{5}{2}+\frac{1}{6}=\frac{377}{32}$