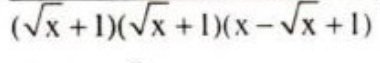Phân số cần tìm là:

Em để ý thấy 2 số hạng đầu nếu đặt \(x\sqrt{x}\) làm nhân tử chung được: \(x\sqrt{x}\left(\sqrt{x}+1\right)\)

Giờ nó lại xuất hiện nhân tử \(\sqrt{x}+1\) với 2 số hạng cuối

Cứ vậy là ra thôi

Ta đặt số thứ nhất là: a

           số thứ 2 là: b

Ta có:

a + b = 92

3a + 5b = 384

(3a + 5b) - (a  + b) = 384 - 92

2a + 4b = 292

a + 2b = 146 (chia cả 2 vế cho 2)

(a + 2b) - (a + b) = 146 - 92

b = 54

a = 92 - 54 = 38

Vậy 2 số ban đầu là: 38 và 54.

Đáp số: 38 và 45

Do số cây bằng nhau nên số cây đó sẽ ϵ B(8; 9)   

                                                               ϵ B(72)

                                                               ϵ {0; 72; 144; 216; ...}

Do số cây là từ 100 - 200 cây nên mỗi đội phải trồng là: 144.

Đáp số: 144

Gọi số học sinh lớp 7A,7B,7C lần lượt là a(bạn),b(bạn),c(bạn)

(Điều kiện: \(a,b,c\in Z^+\))

Số học sinh của lớp 7C lớn hơn số học sinh của lớp 7A là 3 bạn nên c-a=3

Tỉ số giữa số học sinh lớp 7A và 7B là 16:15

=>\(\dfrac{a}{16}=\dfrac{b}{15}\)

=>\(\dfrac{a}{32}=\dfrac{b}{30}\)

Tỉ số giữa số học sinh lớp 7B và 7C là 6:7

=>\(\dfrac{b}{6}=\dfrac{c}{7}\)

=>\(\dfrac{b}{30}=\dfrac{c}{35}\)

Do đó: \(\dfrac{a}{32}=\dfrac{b}{30}=\dfrac{c}{35}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{32}=\dfrac{b}{30}=\dfrac{c}{35}=\dfrac{c-a}{35-32}=1\)

=>a=32;b=30;c=35

Vậy: số học sinh lớp 7A,7B,7C lần lượt là 32(bạn), 30(bạn), 35(bạn)

Help me please 

gọi 2 số cần tìm là a;b

vì tổng 2 số là 92=>a+b=92=>a=92-b.

vì nếu số thứ 1 gấp lên 3 lần và số thứ 2 gấp lên 5 lần thì ta có tổng mới là 384=>3a+5b=384.

thay a=92-b ta có:

3(92-b)+5b=384.

=>276+2b=384.

=>b=(384-276):2=54.

=>a=92-54=38

vậy...

(tick cho mình nhé)

5 lần tổng của hai số cần tìm là: 

`92 x 5 = 460 `

2 lần số thứ nhất là: 

`460 - 384 = 76`

Số thứ nhất là: 

`76 : 2 = 38`

Số thứ hai là: 

`92 - 38 = 54`

Đáp số: ...

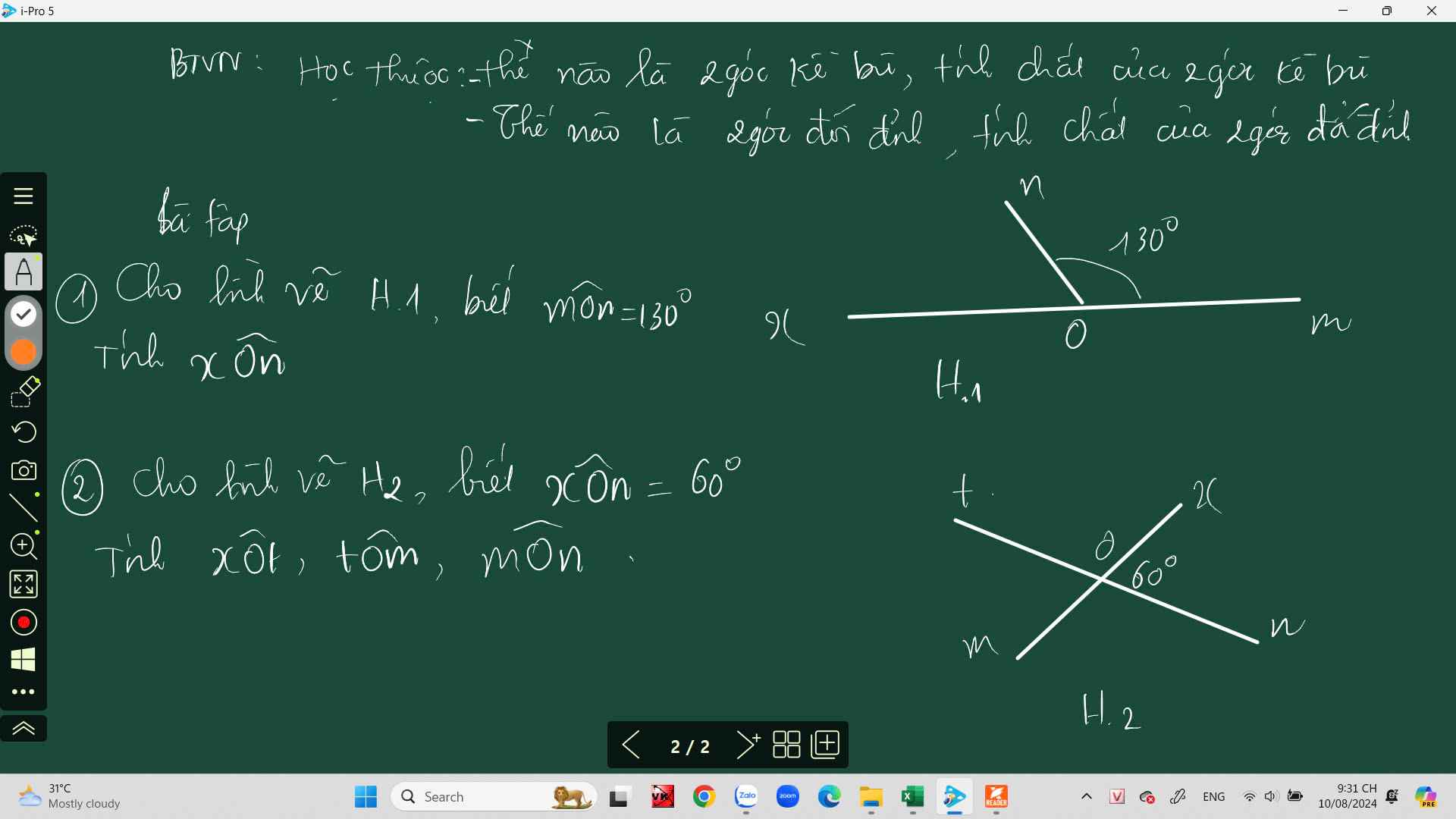
Bài 1: \(\widehat{xOn}+\widehat{mOn}=180^0\)(hai góc kề bù)

=>\(\widehat{xOn}+30^0=180^0\)

=>\(\widehat{xOn}=150^0\)

Bài 2:

Ta có: \(\widehat{xOt}+\widehat{xOn}=180^0\)(hai góc kề bù)

=>\(\widehat{xOt}=180^0-60^0=120^0\)

Ta có: \(\widehat{xOn}=\widehat{tOm}\)(hai góc đối đỉnh)

mà \(\widehat{xOn}=60^0\)

nên \(\widehat{tOm}=60^0\)

Ta có: \(\widehat{xOt}=\widehat{mOn}\)(hai góc đối đỉnh)

mà \(\widehat{xOt}=120^0\)

nên \(\widehat{mOn}=120^0\)

\(1^{2014}=1\) (1)

\(2^{2014}=2^{4.503+2}=\left(2^4\right)^{503}.2^2=16^{503}.4=\overline{...6}.4=\overline{...4}\) (2)

\(3^{2014}=3^{4.503+2}=\left(3^4\right)^{503}.3^2=81^{503}.9=\overline{...1}.9=\overline{...9}\) (3)

\(4^{2014}=4^{2.1007}=\left(4^2\right)^{1007}=16^{1007}=\overline{...6}\) (4)

\(5^{2014}=\overline{...5}\) (5)

\(6^{2014}=\overline{...6}\) (6)

\(7^{2014}=7^{4.503+2}=\left(7^4\right)^{503}.7^2=2401^{503}.49=\overline{...1}.49=\overline{...9}\) (7)

\(8^{2014}=8^{4.503+2}=\left(8^4\right)^{503}.8^2=4096^{503}.64=\overline{...6}.64=\overline{...4}\) (8)

Lấy `(1) + (2)` được số tận cùng là 5 chia hết cho 5

Lấy `(3) + (4)` được số tận cùng là 5 chia hết cho 5

Lấy `(6) + (8)` được số tận cùng là 0 chia hết cho 5

Mà `(5)` có tận cùng là chữ số 5 chia hết cho 5 

Nên  `(1) + (2) +  (3) + (4) + (5) + (6) + (8)` cho kết quả là số chia hết cho 5

Ta có: `(7)` tận cùng là chữ số 9 mà 9 chia 5 dư 4

Vậy phép tính trên chia 5 dư 4

1.371742e+190 đấy :)

sosososos dịch ra là sos os os os

hehe