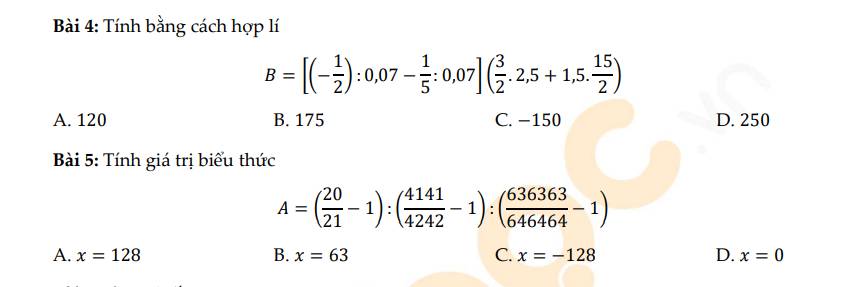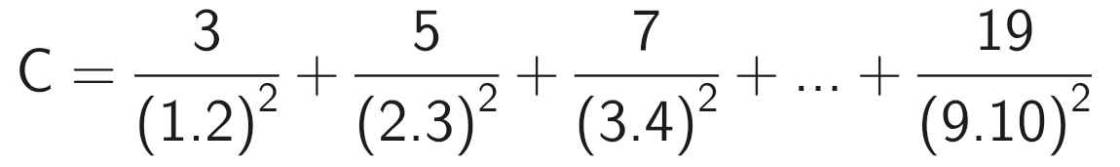
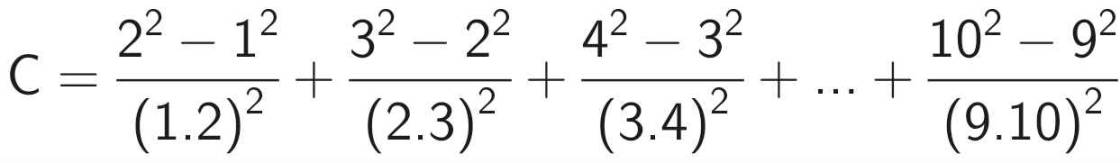
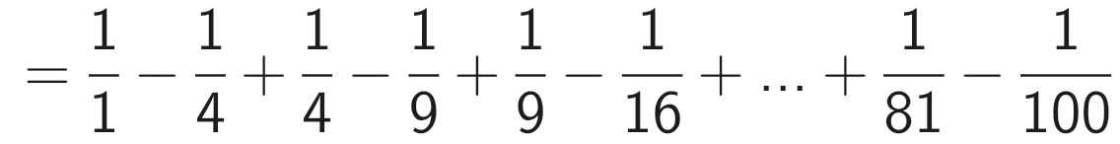
a, \(\dfrac{1}{2}< \dfrac{12}{a}< \dfrac{4}{3}\Leftrightarrow\dfrac{1}{24}< \dfrac{1}{a}< \dfrac{1}{9}\Leftrightarrow9< a< 24\)

b, \(\dfrac{14}{5}< \dfrac{a}{5}< 4\Leftrightarrow14< a< 20\)

a) \(\dfrac{1}{2}< \dfrac{12}{a}< \dfrac{4}{3}\)

\(6\cdot\dfrac{1}{2}< 6\cdot\dfrac{12}{a}< 6\cdot\dfrac{4}{3}\)

\(3< \dfrac{72}{a}< 8\)

\(\dfrac{72}{3}>a>\dfrac{72}{8}\)

\(24>a>9\) 

Vậy: ... 

b) \(\dfrac{14}{5}< \dfrac{a}{5}< 4\)

\(\dfrac{14}{5}\times5< a< 5\times4\)

\(14< a< 20\)

\(\dfrac{ab}{a^2b^3}=\dfrac{1}{ab^2}\)

\(\dfrac{a\cdot b}{b^3\cdot a^2}=\dfrac{1}{ab^2}\)

\(y=\dfrac{a+2}{a-1}=\dfrac{a-1+3}{a-1}=1+\dfrac{3}{a-1}\)

De y nguyen thi 3/a-1 nguyen 

\(a-1\in U\left(3\right)=\left\{\pm1;\pm3\right\}\)

Tập hợp \(M=\left\{3;4;5;6;7\right\}\)

\(8^{11}\cdot9^4\cdot15^6:\left(4^{13}\cdot18^2\cdot3\cdot5^5\right)\)

\(=\left(2^3\right)^{11}\cdot\left(3^2\right)^4\cdot\left(3\cdot5\right)^6:\left[\left(2^2\right)^{13}\cdot\left(2\cdot3^2\right)^2\cdot3\cdot5^5\right]\)

\(=2^{33}\cdot3^8\cdot3^6\cdot5^6:\left(2^{26}\cdot2^2\cdot3^4\cdot3\cdot5^5\right)\)

\(=2^{33}\cdot3^{14}\cdot5^6:\left(2^{28}\cdot3^5\cdot5^5\right)\)

\(=\left(2^{33}:2^{28}\right)\cdot\left(3^{14}:3^5\right)\cdot\left(5^6:5^5\right)\)

\(=2^5\cdot3^9\cdot5\)

Bài 8:

a: Quy luật là số sau bằng số trước cộng thêm 5 đơn vị

b: A={3;5;8;13;18;23;28;33}

Bài 9:

a: Quy luật là số sau bằng số trước cộng thêm 3 đơn vị

b: B={2;5;8;11;14;17;20;23;26;29}

Bài 7:

a: A={6;7;8;9;11}

A={\(x\in\)N|5<x<12}

B={2;3;4;...;11}

B={\(x\in\)N|1<x<12}

b: C={6;7;8;9;11}

\(16^5:8^3\)

\(=\left(2^4\right)^5:\left(2^3\right)^3\)

\(=2^{4\cdot5}:2^{3\cdot3}\)

\(=2^{20}:2^9\)

\(=2^{20-9}\)

\(=2^{11}\)

\(=2048\)

a, A = { n \(\in N\)| 1 =< n =< 5 } 

b, B = { n \(\in\)N| 0 =< n =< 4 } 

c, C = { n \(\in N\)| 1 =< n =< 4 } 

d, D = { \(n\in N\)| 0 =< n =< 3, 2n+2 } 

e, E = { \(n\in\)N| 0 =< n =< 24, 2n+1 }

f, F = { n \(\in\)N| 1 =< n =< 9, 11n }

Bài 2:

a) \(A=\left\{x\in N|1\le x\le5\right\}\) 

b) \(B=\left\{x\in N|0\le x\le4\right\}\)

c) \(C=\left\{x\in N|1\le x\le4\right\}\)

d) \(D=\left\{x=2k|k\in N;0\le k\le4\right\}\)

e) \(E=\left\{x=2k+1|k\in N;0\le k\le21\right\}\)

f) \(F=\left\{x=11k|k\in N;1\le k\le9\right\}\)

Bài 4:

\(B=\left[\left(-\dfrac{1}{2}\right):0,07-\dfrac{1}{5}:0,07\right]\left(\dfrac{3}{2}\cdot2,5+1,5\cdot\dfrac{15}{2}\right)\)

\(=\left[\left(-\dfrac{1}{2}\right)\cdot\dfrac{100}{7}-\dfrac{1}{5}\cdot\dfrac{100}{7}\right]\left(\dfrac{3}{2}\cdot\dfrac{5}{2}+\dfrac{3}{2}\cdot\dfrac{15}{2}\right)\)

\(=\dfrac{100}{7}\cdot\left(-\dfrac{1}{2}-\dfrac{1}{5}\right)\cdot\dfrac{3}{2}\left(\dfrac{5}{2}+\dfrac{15}{2}\right)\)

\(=\dfrac{100}{7}\cdot-\dfrac{7}{10}\cdot\dfrac{3}{2}\cdot\dfrac{20}{2}\)

\(=-10\cdot15\)

\(=-150\)

Chọn C 

Bài 5:

\(A=\left(\dfrac{20}{21}-1\right):\left(\dfrac{4141}{4242}-1\right):\left(\dfrac{636363}{646464}-1\right)\)

\(=\left(1-\dfrac{1}{21}-1\right):\left(\dfrac{41\cdot101}{42\cdot101}-1\right):\left(\dfrac{63\cdot10101}{64\cdot10101}-1\right)\)

\(=\left(-\dfrac{1}{21}\right):\left(\dfrac{41}{42}-1\right):\left(\dfrac{63}{64}-1\right)\)

\(=\left(-\dfrac{1}{21}\right):\left(1-\dfrac{1}{42}-1\right):\left(1-\dfrac{1}{64}-1\right)\)

\(=\left(-\dfrac{1}{21}\right):\left(-\dfrac{1}{42}\right):\left(-\dfrac{1}{64}\right)\)

\(=\left(-\dfrac{1}{21}\right)\cdot\left(-42\right)\cdot\left(-64\right)\)

\(=\left(-\dfrac{1}{21}\cdot-42\right)\cdot64\)

\(=2\cdot64\)

\(=128\)

Chọn A