cho hai số có tổng là 140.Biết 3/5 số thứ nhất thì hơn 1/4 số thứ 2 là 33 đơn vị tìm hai số đó?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8$
$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$
b.
Xét tam giác $AEH$ và $AHB$ có:
$\widehat{A}$ chung
$\widehat{AEH}=\widehat{AHB}=90^0$
$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)
$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$
$\Rightarrow AH^2=AE.AB(1)$
Hoàn toàn tương tự: $\triangle AFH\sim \triangle AHC$
$\Rightarrow AH^2=AF.AC(2)$
Từ $(1); (2)\Rightarrow AE.AB=AF.AC$
c.
$HE\perp AB, AB\perp AC$ nên $HE\parallel AC$
Tam giác vuông $BEH$ vuông tại $E$ có trung tuyến $EM$ ứng với cạnh huyền $BH$
nên $EM=\frac{BH}{2}=MH$
$\Rightarrow EMH$ cân tại $M$
$\Rightarrow \widehat{MEH}=\widehat{MHE}=\widehat{HCA}(3)$ (2 góc đồng vị)
Tứ giác $AEHF$ có 3 góc $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hcn.
$\Rightarrow \widehat{HEF}=\widehat{HAF}=\widehat{HAC}(4)$
Từ $(3); (4)\Rightarrow \widehat{MEH}+\widehat{HEF}=\widehat{HCA}+\widehat{HAC}$
$\Rightarrow \widehat{MEF}=\widehat{HCA}+\widehat{HAC}=90^0$
$\Rightarrow EM\perp EF$

`#3107.101107`
`g)`
\(\dfrac{4}{19}\cdot\dfrac{-3}{7}+\dfrac{-3}{7}\cdot\dfrac{15}{19}+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\left(\dfrac{4}{19}+\dfrac{15}{19}\right)+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\cdot1+\dfrac{5}{7}\)
\(=-\dfrac{3}{7}+\dfrac{5}{7}=\dfrac{2}{7}\)
`h)`
\(\dfrac{5}{9}\cdot\dfrac{7}{13}+\dfrac{5}{9}\cdot\dfrac{9}{13}-\dfrac{5}{9}\cdot\dfrac{3}{13}\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13}\right)\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7+9-3}{13}\right)\)
\(=\dfrac{5}{9}\cdot1=\dfrac{5}{9}\)
`i)`
\(\left(\dfrac{-4}{5}+\dfrac{4}{3}\right)+\left(\dfrac{-5}{4}+\dfrac{14}{5}\right)-\dfrac{7}{3}\)
\(=\dfrac{-4}{5}+\dfrac{4}{3}+\dfrac{-5}{4}+\dfrac{14}{5}-\dfrac{7}{3}\)
\(=\left(-\dfrac{4}{5}+\dfrac{14}{5}\right)+\left(\dfrac{4}{3}-\dfrac{7}{3}\right)-\dfrac{5}{4}\)
\(=\dfrac{10}{5}+\dfrac{-3}{3}-\dfrac{5}{4}\)
\(=2-1-\dfrac{5}{4}\)
\(=1-\dfrac{5}{4}\)
\(=-\dfrac{1}{4}\)
`j)`
\(\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\)
\(=\left(\dfrac{8}{3}\cdot\dfrac{3}{8}\right)\cdot\left(\dfrac{2}{5}\cdot10\right)\cdot\dfrac{19}{92}\)
\(=1\cdot\dfrac{20}{5}\cdot\dfrac{19}{92}\)
\(=4\cdot\dfrac{19}{92}=\dfrac{19}{23}\)
`k)`
\(\dfrac{-5}{7}\cdot\dfrac{2}{11}+\dfrac{-5}{7}\cdot\dfrac{9}{14}+1\dfrac{5}{7}\)
\(=-\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{9}{14}+1+\dfrac{5}{7}\)
\(=\dfrac{5}{7}\cdot\left(-\dfrac{2}{11}-\dfrac{9}{14}+1\right)+1\)
\(=\dfrac{5}{7}\cdot\dfrac{27}{154}+1\)
\(=\dfrac{135}{1078}+1=\dfrac{1213}{1078}\)
`l)`
\(\dfrac{12}{19}\cdot\dfrac{7}{15}\cdot\dfrac{-13}{17}\cdot\dfrac{19}{12}\cdot\dfrac{17}{13}\)
\(=\left(\dfrac{12}{19}\cdot\dfrac{19}{12}\right)\cdot\left(-\dfrac{13}{17}\cdot\dfrac{17}{13}\right)\cdot\dfrac{7}{15}\)
\(=1\cdot\left(-1\right)\cdot\dfrac{7}{15}=-\dfrac{7}{15}\)

Giải:
Từ 1 đến 112 có các số lẻ là các số lần lượt thuộc dãy số sau:
1; 3; 5; 7; 9; 11;...; 111
Đây là dãy số cách đều với khoảng cách là:
3 - 1 = 2
Dãy số trên có số các số hạng là:
(111 - 1) : 2 + 1 = 56 (số hạng)
Vậy từ 1 đến 112 có 56 số lẻ
Đáp số: 56 số lẻ

a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>CD\(\perp\)AB tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)AC tại E
Xét ΔABC có
BE,CD là các đường cao
BE cắt CD tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
Xét tứ giác HECF có \(\widehat{HEC}+\widehat{HFC}=90^0+90^0=180^0\)
nên HECF là tứ giác nội tiếp
=>\(\widehat{HEF}=\widehat{HCF}\)
b: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
nên ADHE là tứ giác nội tiếp
=>\(\widehat{DEH}=\widehat{DAH}\)
mà \(\widehat{HEF}=\widehat{HCF}\)
và \(\widehat{DAH}=\widehat{HCF}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{DEB}=\widehat{FEB}\)
=>EB là phân giác của góc DEF

a: Để hàm số y=(m-2)x+m+3 đồng biến thì m-2>0
=>m>2
b: Để đồ thị hàm số y=(m-2)x+m+3 song song với đường thẳng y=2x+7 thì
\(\left\{{}\begin{matrix}m-2=2\\m+3\ne7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=4\\m\ne4\end{matrix}\right.\)
=>\(m\in\varnothing\)
Hàm số y = (m + 2)x + 3 là hàm số bậc nhất khi m + 2 ≠ 0, hay m ≠ – 2.
Vậy ta có điều kiện m ≠ – 2.
a) Đồ thị hàm số đã cho song song với đường thẳng y = –x khi m + 2 = –1, tức là m = –3.
Giá trị này thỏa mãn điều kiện m ≠ – 2.
Vậy giá trị m cần tìm là m = –3.
b) Với m = –3 ta có hàm số y = –x + 3.
Đồ thị hàm số y = –x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0).
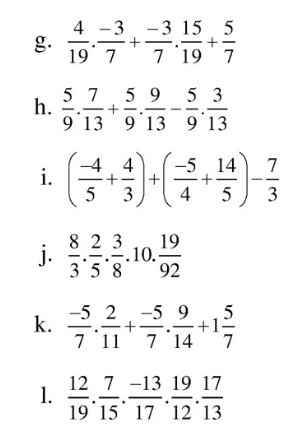
Đây là dạng toán nâng cao chuyên đề toán hai tỉ số, cấu trúc thi chuyên thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ như sau:
Giải:
\(\dfrac{3}{5}\) số thứ nhất và \(\dfrac{3}{5}\) số thứ hai là: 140 x \(\dfrac{3}{5}\) = 84
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
\(\dfrac{1}{4}\) số thứ hai và \(\dfrac{3}{5}\) số thứ hai là: 84 - 33 = 51
51 ứng với: \(\dfrac{1}{4}\) + \(\dfrac{3}{5}\) = \(\dfrac{17}{20}\) (số thứ hai)
Số thứ hai là: 51 : \(\dfrac{17}{20}\) = 60
Số thứ nhất là: 140 - 60 = 80
Đáp số: số thứ nhất 80
số thứ hai 60
Lời giải:
Gọi số thứ nhất là $a$ và số thứ hai là $b$. Theo bài ra ta có:
$a+b=140$
$a=140-b$
$\frac{3}{5}\times a-\frac{1}{4}\times b=33$
Thay $a=140-b$ vào điều kiện trên thì:
$\frac{3}{5}\times (140-b)-\frac{1}{4}\times b=33$
$84-\frac{3}{5}\times b-\frac{1}{4}\times b=33$
$84-b\times (\frac{3}{5}+\frac{1}{4})=33$
$84-b\times \frac{17}{20}=33$
$b\times \frac{17}{20}=84-33=51$
$b=51:\frac{17}{20}=60$
$a=140-b=140-60=80$
Vậy hai số cần tìm là $80$ và $60$