
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Áp dụng BĐT Cô-si:
$\frac{x^3}{y^2}+y+y\geq 3\sqrt[3]{x^3}=3x$
$\frac{y^3}{z^2}+z+z\geq 3\sqrt[3]{y^3}=3y$
$\frac{z^3}{x^2}+x+x\geq 3\sqrt[3]{z^3}=3z$
Cộng 3 BĐT trên theo vế và thu gọn thì:
$P+2(x+y+z)\geq 3(x+y+z)$
$\Rightarrow P\geq x+y+z=2023$
Vậy $P_{\min}=2023$. Giá trị này đạt tại $x=y=z=\frac{2023}{3}$
Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn và hỗ trợ tốt hơn nhé.

Câu 6:
a: ĐKXĐ: \(x\notin\left\{0;3;2;-2\right\}\)
\(A=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\left(\dfrac{x^2-3x}{2x^2-x^3}\right)\)
\(=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right):\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{-\left(x+2\right)^2-4x^2+\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x+2\right)}\cdot\dfrac{-x}{x-3}\)
\(=\dfrac{-4x^2-8x}{\left(x+2\right)}\cdot\dfrac{-x}{x-3}=\dfrac{4x^2+8x}{x+2}\cdot\dfrac{x}{x-3}\)
\(=\dfrac{4x^2}{x-3}\)
b: Để A>0 thì \(\dfrac{4x^2}{x-3}>0\)
=>x-3>0
=>x>3
c: |x-7|=4
=>\(\left[{}\begin{matrix}x-7=4\\x-7=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=11\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
Thay x=11 vào A, ta được:
\(A=\dfrac{4\cdot11^2}{11-3}=\dfrac{4\cdot121}{8}=\dfrac{121}{2}\)

I: Trắc nghiệm
Câu 1: C
Câu 2: A
Câu 3: D
Câu 4: A
II: Tự luận
Câu 5:
a: ĐKXĐ: x<>-1/2
\(\dfrac{5-3x}{2x+1}-\dfrac{-2+5x}{2x+1}\)
\(=\dfrac{5-3x+2-5x}{2x+1}\)
\(=\dfrac{-8x+7}{2x+1}\)
b: ĐKXĐ: x<>-1
\(\dfrac{3}{x+1}-\dfrac{2+3x^2}{x^3+1}\)
\(=\dfrac{3}{x+1}-\dfrac{3x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{3\left(x^2-x+1\right)-3x^2-2}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{-3x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)

Câu 6(Đề 4)
a: \(A=\left(\dfrac{3x^2+3}{x^3-1}-\dfrac{x-1}{x^2+x+1}-\dfrac{1}{x-1}\right):\dfrac{2x^2-5x+5}{x-1}\)
\(=\left(\dfrac{3x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x-1}{x^2+x+1}-\dfrac{1}{x-1}\right)\cdot\dfrac{x-1}{2x^2-5x+5}\)
\(=\dfrac{3x^2+3-\left(x-1\right)^2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{2x^2-5x+5}\)
\(=\dfrac{2x^2-x+2-x^2+2x-1}{x^2+x+1}\cdot\dfrac{1}{2x^2-5x+5}\)
\(=\dfrac{x^2+x+1}{x^2+x+1}\cdot\dfrac{1}{2x^2-5x+5}=\dfrac{1}{2x^2-5x+5}\)
b: \(2x^2-5x+5=2\left(x^2-\dfrac{5}{2}x+\dfrac{5}{2}\right)\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{15}{16}\right)\)
\(=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{15}{8}>=\dfrac{15}{8}\forall x\)
=>\(A=\dfrac{1}{2x^2-5x+5}< =1:\dfrac{15}{8}=\dfrac{8}{15}\forall x\)
Dấu '=' xảy ra khi x=5/4

I: Trắc nghiệm:
Câu 1: C
Câu 2: D
Câu 3: B
Câu 4: A
II: tự luận
Câu 5:
a: ĐKXĐ: x<>-2
\(\dfrac{2-x}{x+2}+\dfrac{x}{x+2}=\dfrac{2-x+x}{x+2}=\dfrac{2}{x+2}\)
b: ĐKXĐ: y<>2x
\(\dfrac{2x}{2x-y}+\dfrac{y}{y-2x}\)
\(=\dfrac{2x}{2x-y}-\dfrac{y}{2x-y}\)
\(=\dfrac{2x-y}{2x-y}=1\)

\(\left(d\right)y=\left(3m+1\right)x+m-3\left(m\ne-\dfrac{1}{3}\right)\); \(\left(d'\right)y=-5x+m-1\)
a) Để (d) đồng biến trên R thì:
\(3m+1>0\)
\(\Leftrightarrow3m>-1\)
\(\Leftrightarrow m>-\dfrac{1}{3}\)
b) Để (d) // (d') thì \(3m+1=-5\)
\(\Leftrightarrow3m=-6\)
\(\Leftrightarrow m=-2\)

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB~ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
b: Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\widehat{DAE}\) chung
Do đó: ΔADE~ΔABC
c: Ta có: ΔADE~ΔABC
=>\(\widehat{AED}=\widehat{ACB}\)
mà \(\widehat{AED}=\widehat{IEB}\)(hai góc đối đỉnh)
nên \(\widehat{IEB}=\widehat{ICD}\)
Xét ΔIEB và ΔICD có
\(\widehat{IEB}=\widehat{ICD}\)
\(\widehat{I}\) chung
Do đó: ΔIEB~ΔICD
=>\(\dfrac{IE}{IC}=\dfrac{IB}{ID}\)
=>\(IE\cdot ID=IB\cdot IC\)

Bài 3:
a: Xét ΔCNB vuông tại N và ΔCMA vuông tại M có
\(\widehat{C}\) chung
Do đó: ΔCNB~ΔCMA
=>\(\dfrac{CN}{CM}=\dfrac{CB}{CA}\)
=>\(CN\cdot CA=CM\cdot CB\)
b: Xét ΔANH vuông tại N và ΔAMC vuông tại M có
\(\widehat{NAH}\) chung
Do đó: ΔANH~ΔAMC
=>\(\dfrac{AN}{AM}=\dfrac{AH}{AC}\)
=>\(AN\cdot AC=AH\cdot AM\)
Bài 2:
Xét ΔOAE và ΔODB có
\(\dfrac{OA}{OD}=\dfrac{OE}{OB}\left(\dfrac{2}{3}=\dfrac{6}{9}\right)\)
\(\widehat{O}\) chung
Do đó: ΔOAE~ΔODB
=>\(\widehat{OEA}=\widehat{OBD}\)
Bài 1:
a: \(AH^2=HB\cdot HC\)
=>\(\dfrac{AH}{HB}=\dfrac{HC}{AH}\)
Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
\(\dfrac{HA}{HB}=\dfrac{HC}{HA}\)
Do đó: ΔHAC~ΔHBA
b: Ta có: ΔHAC~ΔHBA
=>\(\widehat{HAC}=\widehat{HBA}\)
mà \(\widehat{HAC}+\widehat{C}=90^0\)(ΔHAC vuông tại H)
nên \(\widehat{B}+\widehat{C}=90^0\)
=>ΔABC vuông tại A







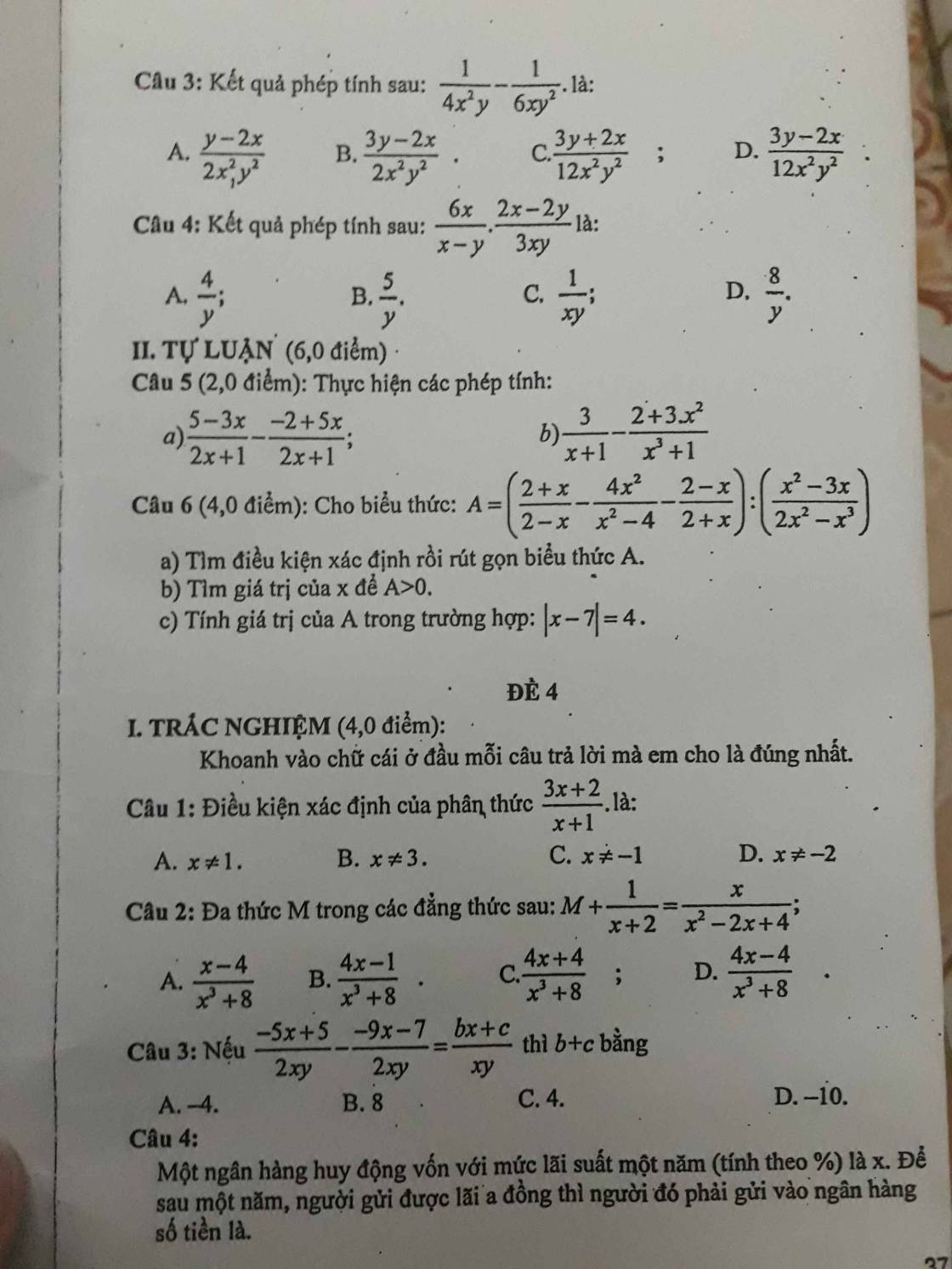



a) \(\dfrac{1+\dfrac{1}{x}}{x-\dfrac{1}{x}}=\dfrac{\dfrac{x+1}{x}}{\dfrac{x^2-1}{x}}=\dfrac{x+1}{x^2-1}=\dfrac{x+1}{\left(x+1\right)\left(x-1\right)}=\dfrac{1}{x-1}\left(x\ne0;x\ne1;x\ne-1\right)\)
b) \(\left(\dfrac{1}{x^2+4x+4}-\dfrac{1}{x^2-4x+4}\right):\left(\dfrac{1}{x+2}+\dfrac{1}{x-2}\right)\left(x\ne\pm2\right)\)
\(=\left[\dfrac{1}{\left(x+2\right)^2}-\dfrac{1}{\left(x-2\right)^2}\right]:\left(\dfrac{1}{x+2}+\dfrac{1}{x-2}\right)\)
\(=\dfrac{\left(\dfrac{1}{x+2}\right)^2-\left(\dfrac{1}{x-2}\right)^2}{\dfrac{1}{x+2}+\dfrac{1}{x-2}}\)
\(=\dfrac{\left(\dfrac{1}{x+2}-\dfrac{1}{x-2}\right)\left(\dfrac{1}{x+2}+\dfrac{1}{x-2}\right)}{\dfrac{1}{x+2}+\dfrac{1}{x-2}}\)
\(=\dfrac{1}{x+2}-\dfrac{1}{x-2}\)
\(=\dfrac{x-2-x-2}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{-4}{x^2-4}\)
c: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\left(\dfrac{x}{x+1}+1\right):\left(1-\dfrac{3x^2}{1-x^2}\right)\)
\(=\dfrac{x+x+1}{x+1}:\dfrac{1-x^2-3x^2}{1-x^2}\)
\(=\dfrac{2x+1}{x+1}\cdot\dfrac{x^2-1}{4x^2-1}\)
\(=\dfrac{2x+1}{x+1}\cdot\left(x-1\right)\cdot\dfrac{\left(x+1\right)}{\left(2x-1\right)\left(2x+1\right)}\)
\(=\dfrac{\left(x-1\right)}{2x-1}\)
d:
ĐKXĐ: x<>1
\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)
\(=\dfrac{3x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x-1}{x^2+x+1}\)
\(=\dfrac{3x+\left(x-1\right)^2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x-1}\)
e: ĐKXĐ: \(x\notin\left\{1;0;-1\right\}\)
\(\dfrac{1}{x-1}-\dfrac{x^3-x}{x^2+x}\left(\dfrac{1}{x^2-2x+1}+\dfrac{1}{1-x^3}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}\cdot\left(\dfrac{1}{\left(x-1\right)^2}-\dfrac{1}{\left(x-1\right)\left(x^2+x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\left(x-1\right)\cdot\left(\dfrac{x^2+x+1-\left(x-1\right)}{\left(x-1\right)^2\cdot\left(x^2+x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x^2+x+1-x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1-x^2-2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)