Ta thực hiện theo các bước sau:

Bước 1. Xác định ba điểm A, B, C nằm trên rìa mảnh gỗ .

Bước 2. Xác định ba đường trung trực của tam giác ABC.

Bước 3. Xác định giao điểm của ba đường trung trực của tam giác ABC.

Điểm đó là tâm của mảnh gỗ

Em cần làm gì với biểu thức này!

giúp mình với

Sửa đề:

ABC cân tại A có BH và CK là hai đường cao

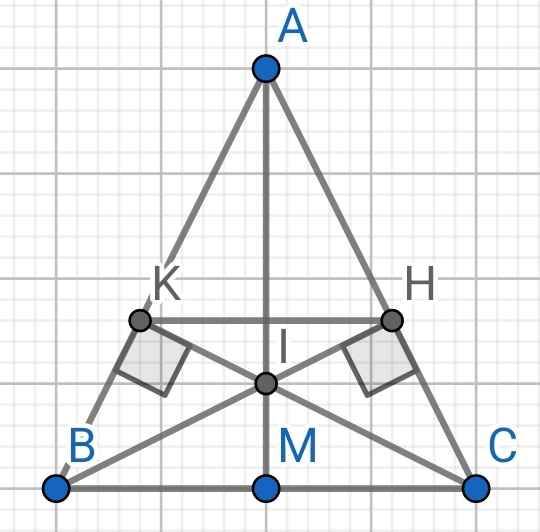
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆AHB và ∆AKC có:

AB = AC (cmt)

∠A chung

⇒ ∆AHB = ∆AKC (cạnh huyền - góc nhọn)

⇒ AH = AK (hai cạnh tương ứng)

⇒ ∆AKH cân tại A

b) ∆ABC cân tại A (gt)

BH và CK là hai đường cao cắt nhau tại I (gt)

⇒ AI là đường cao thứ ba

⇒ AI ⊥ BC

⇒ IM ⊥ BC

Do ∆ABC cân tại A có

AI là đường cao (cmt)

⇒ AM là đường cao

⇒ AM cũng là đường trung tuyến

⇒ M là trung điểm của BC

⇒ MB = MC

Xét hai tam giác vuông: ∆IBM và ∆ICM có:

IM là cạnh chung

MB = MC (cmt)

⇒ ∆IBM = ∆ICM (hai cạnh góc vuông)

⇒ ∠BIM = ∠CIM (hai góc tương ứng)

⇒ IM là tia phân giác của ∠BIC

c) Xét hai tam giác vuông: ∆AHI và ∆AKI có:

AI là cạnh chung

AH = AK (cmt)

⇒ ∆AHI = ∆AKI (cạnh huyền - cạnh góc vuông)

⇒ IH = IK (hai cạnh tương ứng)

⇒ I nằm trên đường trung trực của HK (1)

Do AH = AK (cmt)

⇒ A nằm trên đường trung trực của HK (2)

Từ (1) và (2) ⇒ AI là đường trung trực của HK

⇒ AI ⊥ HK

Lại có:

AI ⊥ BC (cmt)

⇒ HK // BC

\(\left(x+3\right)\left(x-1\right)=x\left(x-1\right)+3\left(x-1\right)=x^2-x+3x-3=x^2+2x-3\)

\(\left(3x^3-2x^2\right):3x^2=3x^3:3x^2-2x^2:3x^2=x-\dfrac{2}{3}\)

Đề bài sai, ví dụ với \(n=4\) thì \(n^2-3n+4=8\) ko chia hết \(n-1=3\)

a: Xét ΔABC có AB>AC
mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của cạnh AB,AC

nên \(\widehat{ACB}>\widehat{ABC}\)

b: ΔACF cân tại A

mà AE là đường phân giác

nên AE là đường trung trực của CF

trung điểm

trung điểm

\(B\left(x\right)=x^2-5x-3x^2+1+x-5\)

\(=\left(x^2-3x^2\right)+\left(-5x+x\right)+1-5\)

\(=-2x^2-4x-4\)

Để thu gọn biểu thức \( b(x) = x^2 - 5x - 3x^2 + 1 + x - 5 \), ta cần thực hiện các bước sau:

1. Kết hợp các thành phần giống nhau (cùng bậc) của biểu thức.
2. Tính tổng các hạng tử.

Bước 1: Kết hợp các thành phần giống nhau:
\[ b(x) = (x^2 - 3x^2) + (-5x + x) + (1 - 5) \]

Bước 2: Tính tổng các hạng tử:
\[ b(x) = (-2x^2) + (-4x) + (-4) \]

Vậy, kết quả thu gọn của \( b(x) \) là \( -2x^2 - 4x - 4 \).

a: Chiều dài sau khi mở rộng là x+10(m)

Chiều rộng sau khi mở rộng là x+3(m)

Diện tích khu đất sau khi mở rộng là:

\(S=\left(x+10\right)\left(x+3\right)\left(m^2\right)\)

b: Khi x=20 thì \(S=\left(20+10\right)\left(20+3\right)=30\cdot23=690\left(m^2\right)\)

a) Để tính diện tích khu đất sau khi mở rộng theo chiều dài \( x \), chúng ta cần tính diện tích hình chữ nhật mới.

Ban đầu, diện tích hình vuông là \( x^2 \) (vì cạnh vuông là \( x \)).

Sau khi mở rộng, chiều dài là \( x + 3 \) mét và chiều rộng là \( x + 10 \) mét, do đó diện tích hình chữ nhật mới là \( (x + 3) \times (x + 10) \).

Vậy, diện tích khu đất sau khi mở rộng theo \( x \) là \( (x + 3) \times (x + 10) \).

b) Khi \( x = 20 \), ta thay \( x \) bằng 20 vào công thức ở phần a) để tính diện tích khu đất sau khi mở rộng.
\[ \text{Diện tích khu đất} = (20 + 3) \times (20 + 10) \]
\[ = 23 \times 30 \]
\[ = 690 \text{ mét vuông}^2 \]

Vậy, khi \( x = 20 \), diện tích khu đất sau khi mở rộng là 690 mét vuông.