aaa + mmm + nnn

= a x 111 + m x 111 + n x 111

= 111 x (a + m + n) 

`overline{aaa} + overline{mmm} + overline{nnn} `

`= 111 a + 111m + 111n`

`= 111(a+m+n)`

Đề là \(\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\ge9\) với đúng chứ em?

thầy trả lời giúp em với

Gọi số đó là \(\overline{xy}\) (với x;y là các chữ số từ 0 tới 9, `x \neq 0`)

Do tổng 2 chữ số bằng 9 nên: \(x+y=9\) (1)

Số mới sau khi viết thêm chữ số 0 vào giữa: \(\overline{x0y}\)

Do số mới gấp 9 lần số cũ nên:

\(\overline{x0y}=9\overline{xy}\Leftrightarrow100x+y=9\left(10x+y\right)\)

\(\Leftrightarrow10x-8y=0\) (2)

Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}x+y=9\\10x-8y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\)

Vậy số đó là 45

Gọi số đó là `overline{ab} (a ne 0)`

`=> overline{a0b} = 9 . overline{ab}`

`=> b ∈ {0; 5}`

Xét `b = 0`

thì: `overline{a0} . 9 = overline{a00}`

`=> overline{a0} = overline{a00} : 9`

Hay `overline{a00} vdots 9`

`<=> a + 0 + 0 vdots 9`

`<=> a = 9`

Khi đó:  `overline{a00} : 9 = 900 : 9 = 100` (không thỏa mãn)

Xét `b = 5`

thì: `overline{a5} . 9 = overline{a05}`

`=> overline{a5} = overline{a05} : 9`

Hay `overline{a05} vdots 9`

`<=> a + 0 + 5 vdots 9`

`<=> a = 4`

Khi đó:  `overline{a05} : 9 = 405 : 9 = 45` (Thỏa mãn)

Vậy số đó là `45`

\(A=\left(x+1\right)+\left(x+\dfrac{5}{45}\right)+\left(x+\dfrac{5}{117}\right)+\left(x+221\right)=10\\ \Rightarrow x+1+x+\dfrac{1}{9}+x+\dfrac{5}{117}+x+221=10\\ \Rightarrow4x+\left(1+\dfrac{1}{9}+\dfrac{5}{117}+221\right)=10\\ \Rightarrow4x+\dfrac{2888}{13}=10\\ \Rightarrow4x=10-\dfrac{2888}{13}\\ \Rightarrow4x=-\dfrac{2758}{13}\\ \Rightarrow x=-\dfrac{1379}{26}\)

Cho hỏi 1/9 ở đâu v ak

\(1)-\dfrac{3}{7}+\dfrac{5}{13}-\dfrac{4}{7}+\dfrac{8}{13}\\ =\left(\dfrac{-3}{7}+\dfrac{-4}{7}\right)+\left(\dfrac{5}{13}+\dfrac{8}{13}\right)\\ =\dfrac{-7}{7}+\dfrac{13}{13}\\ =-1+1\\ =0\\ 2)-\dfrac{5}{14}-\dfrac{2}{14}+\dfrac{1}{8}+\dfrac{1}{8}\\ =\left(\dfrac{-5}{14}-\dfrac{2}{14}\right)+\left(\dfrac{1}{8}+\dfrac{1}{8}\right)\\ =\dfrac{-7}{14}+\dfrac{2}{8}\\ =\dfrac{-1}{2}+\dfrac{1}{4}\\ =\dfrac{-1}{4}\\ 3)\dfrac{-5}{22}-1+\dfrac{3}{2}-\dfrac{6}{22}\\ =\left(\dfrac{-5}{22}-\dfrac{6}{22}\right)+\left(\dfrac{3}{2}-1\right)\\ =\dfrac{-11}{22}+\dfrac{1}{2}\\ =\dfrac{-1}{2}+\dfrac{1}{2}\\ =0\)

\(4,\dfrac{7}{16}+\dfrac{5}{9}+\dfrac{-3}{16}+\dfrac{-2}{9}\\ =\left(\dfrac{7}{16}-\dfrac{3}{16}\right)+\left(\dfrac{5}{9}-\dfrac{2}{9}\right)\\ =\dfrac{4}{16}+\dfrac{3}{9}\\ =\dfrac{1}{4}+\dfrac{1}{3}\\ =\dfrac{7}{12}\\ 5,\dfrac{2}{5}-\dfrac{3}{11}-\dfrac{7}{35}+\dfrac{14}{11}-\dfrac{1}{5}\\ =\left(-\dfrac{3}{11}+\dfrac{14}{11}\right)+\left(\dfrac{2}{5}-\dfrac{1}{5}\right)-\dfrac{7}{35}\\ =\dfrac{11}{11}+\dfrac{1}{5}-\dfrac{7}{35}\\ =1+\dfrac{1}{5}-\dfrac{1}{5}\\ =1\\ 6,\dfrac{3}{4}-\dfrac{3}{17}+\dfrac{-5}{6}+\dfrac{20}{17}-\dfrac{1}{4}\\ =\left(\dfrac{3}{4}-\dfrac{1}{4}\right)+\left(\dfrac{-3}{17}+\dfrac{20}{17}\right)+\dfrac{-5}{6}\\ =\dfrac{1}{2}+1+\dfrac{-5}{6}\\ =\dfrac{3}{2}-\dfrac{5}{6}\\ =\dfrac{9}{6}-\dfrac{5}{6}\\ =\dfrac{4}{6}=\dfrac{2}{3}\)

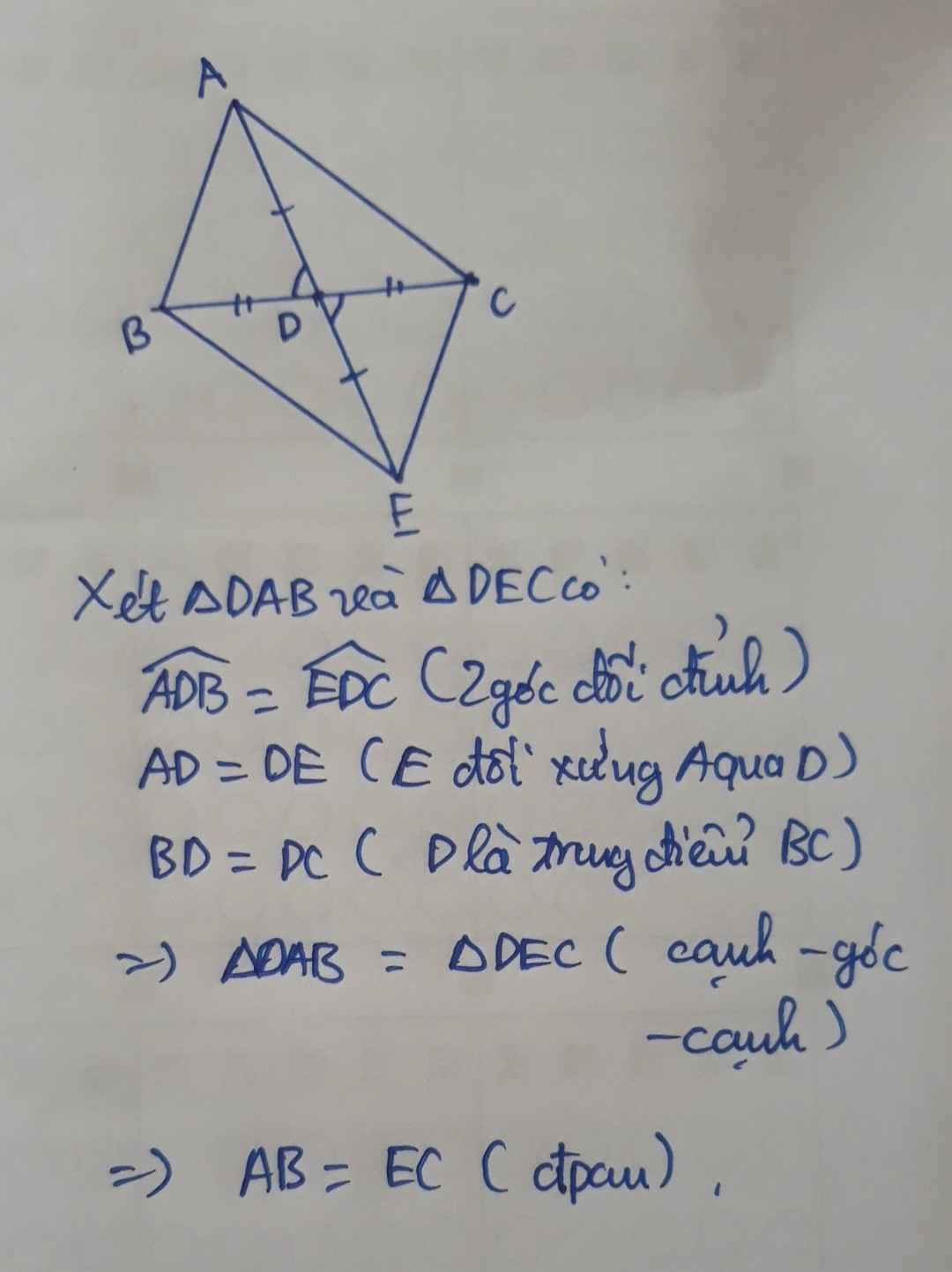
Do E đối xứng A qua D \(\Rightarrow D\) là trung điểm AE

Mà D là trung điểm BC

\(\Rightarrow AE\) và BC cắt nhau tại trung điểm D của mỗi đường

\(\Rightarrow ABEC\) là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)

\(\Rightarrow AB=CE\)

Ta có : tam giác ABC cân tại A có AM là tia phân giác 

=> AM vừa là phân giác vừa là đường cao 

=> AM vuông góc vs BC 

=> C,M,B thẳng hàng

\(\Leftrightarrow\left(6x^2+2xy-8x\right)+\left(3xy+y^2-4y\right)+\left(3x+y-4\right)=1\)

\(\Leftrightarrow2x\left(3x+y-4\right)+y\left(3x+y-4\right)+\left(3x+y-4\right)=1\)

\(\Leftrightarrow\left(3x+y-4\right)\left(2x+y+1\right)=1\)

Pt ước số đơn giản, em có thể tự lập bảng giá trị

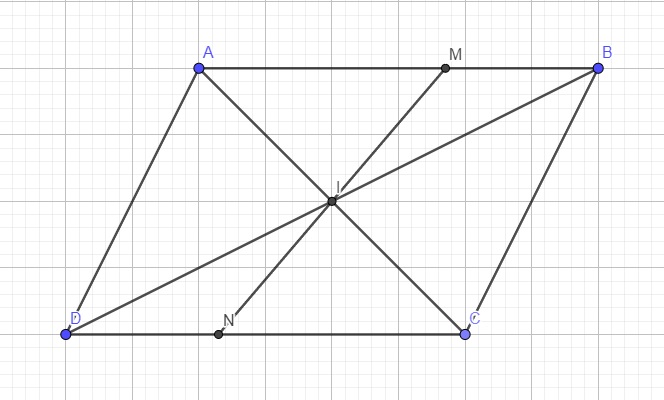
Do I là giao điểm của AC và BD \(\Rightarrow\) I là trung điểm BD

\(\Rightarrow IB=ID\)

Xét hai tam giác IMB và IND có: 

\(\left\{{}\begin{matrix}\widehat{IBM}=\widehat{IDN}\left(\text{so le trong}\right)\\IB=ID\\\widehat{MIB}=\widehat{NID}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)  

\(\Rightarrow\Delta IMD=\Delta IND\left(g.c.g\right)\Rightarrow IM=IN\)

\(A=\left\{n^2\text{ }|\text{ }n\in N,\text{ }1\le n\le7\text{ }\right\}\)

Hoặc:

\(A=\left\{x\text{ }|\text{ }\text{x là số chính phương},\text{ }0< x< 50\right\}\)