|
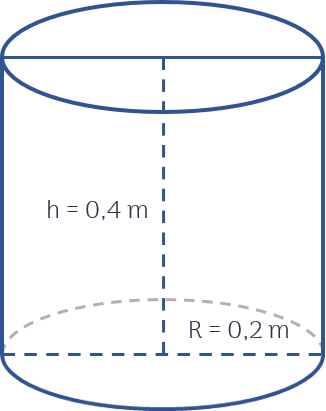
Anh Minh vừa mới xây một cái hồ trữ nước cạnh nhà có hình hộp chữ nhật kích thước $2m \times 2m \times 1m$. Hiện hồ chưa có nước nên anh Minh phải ra sông lấy nước. Mỗi lần ra sông anh gánh được 1 đôi nước đầy gồm hai thùng hình trụ bằng nhau có kích thước đáy $0,2m$, chiều cao $0, 4m$. a. Tính lượng nước ($m^3$) anh Minh đổ vào hồ sau mỗi lần gánh (ghi kết quả làm tròn đến hai chữ số thập phân). Biết trong quá trình gánh nước về hao hụt khoảng $10\%$ và công thức tính thể tích hình trụ là $V = \pi R^2h$. b. Hỏi anh Minh phải gánh ít nhất bao nhiêu lần để đầy hồ? Bỏ qua thể tích thành hồ. |
 |





a, Tính lượng nước \(\left(m^3\right)\)anh Minh đổ vào hố sau mỗi làn gánh ( ghi kết quả làm tròn đến 2 chữ số thập phân )
Biết trong quá trình gánh nước thì lượng nước bị hao hụt khoảng 10% nên
Công thức tính thể tích hình trụ là : \(V=ttR^2h\)
Thể tích của 2 thùng nước mỗi lần anh Minh gánh được là :
\(V_1=2ttR^2h=2tt\times0,0^2\times0,4=0,032tt\left(m^3\right)\)
Trong quá trình gánh , lượng nước hao hụt 10% nên lượng nước thực tế anh Minh đổ vào hồ sau mỗi lần gánh là :
\(V=0,032tt\times90\%=0,09\left(m^3\right)\)
b, Thể tích của hồ nước hình chữ nhật là :
\(V_0=2\times2\times1=4\left(m^3\right)\)
Số lần ít nhất anh Minh cần gánh để đổ đầy hồ nước là :
\(n=[\frac{V_0}{V}]+1=[\frac{4}{0,09}]+1=44+1=45\)Lần
Vtrụ = 0,05 mét khối
V = 0,09 mét khối