Câu 17: Tìm $x$ sao cho $\dfrac{x+2022}{\sqrt{25}}-\dfrac{x+|-2022|}{3}=\dfrac{x}{2}+1011$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


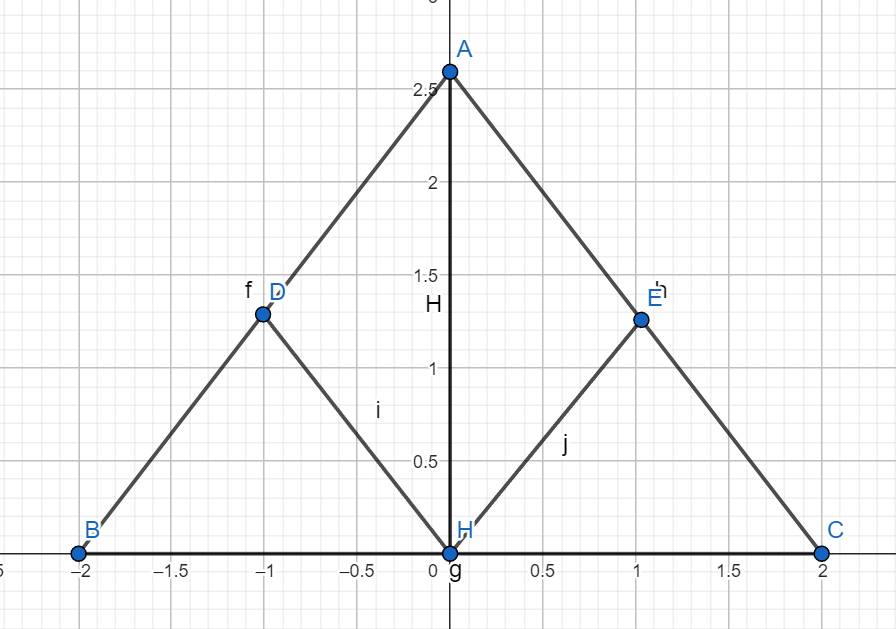
a) Xét ΔABH và ΔACH có:
AH cạnh chung
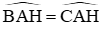
AB = AC (gt)
=> ΔABH = ΔACH (c – g – c)
c.
Gọi I là giao điểm của AH và DE
Xét hai tam giác vuông: ΔADH và ΔAEH có:
AH cạnh chung
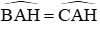
Suy ra: ΔADH = ΔAEH (ch – gn)
Xét ΔADI và ΔAEI có:
AI: cạnh chung
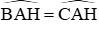
AD = AE (ΔADH = ΔAEH)
=> ΔADI = ΔAEI (c – g – c)
=>\(\left\{{}\begin{matrix}AD=AE\\\widehat{DAI}=\widehat{EAI}\end{matrix}\right.\)
Xét tam giác ADH và tam giác AEH có:
AD = AE
góc DAI = góc EAI
=> tam giác ADH = tam giác AEH (c.g.c)
=> HD = HE (đcpcm)

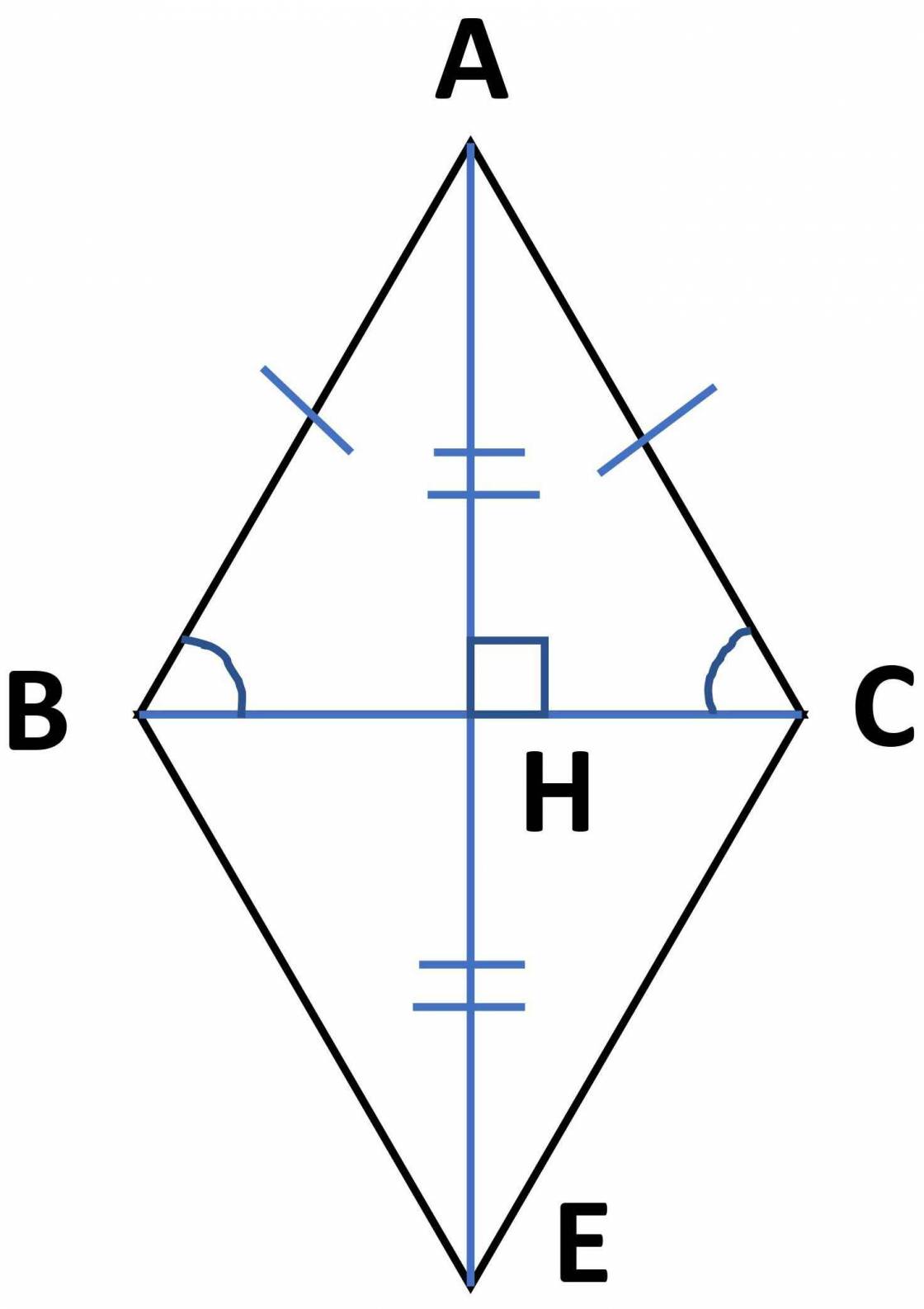
a)
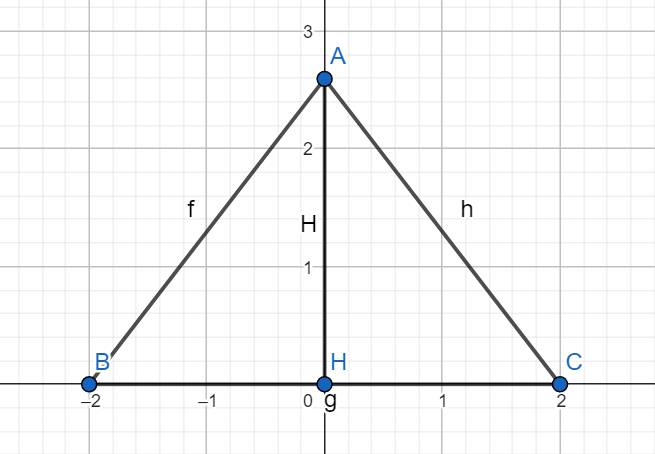
Vì △ABC có AB = AC
\(\rightarrow\)B = C
\(\rightarrow\) △ABC là tam giác cân (2 cạnh đáy bằng nhau)
Xét △ABH và △ ACH có:
AC chung
AB = AC (gt)
BH = CH (H là trung điểm của BC)
\(\Rightarrow\) △ABH = △ACH
b)
Có △ABH = △ACH (câu a)
\(\rightarrow\)góc BAH = góc CAH(2 góc tương ứng)
Mà góc BAH + góc CAH = 180 độ (2 góc kề bù)
\(\rightarrow\) góc BAH = góc CAH = 90 độ
\(\Rightarrow\) AH ⊥ BC
c)

a) Hình vuông với diện tích cm có độ dài cạnh bằng .
Sử dụng MTCT ta tính được
Làm tròn kết quả đến cữ số thập phân thứ hai ta được độ dài cạnh hình vuông cần tính là cm.
b) Uớc lượng số liệu với độ chính xác nên phải làm tròn số đến hàng nghìn.
Số dân thành phố uớc tính là người.
a) Hình vuông với diện tích cm có độ dài cạnh bằng: \(\sqrt{10}\)
-sử dung máy tính cầm tay ta tính được \(\sqrt{10}\)=3,4622...
Làm tròn kết quả đến cữ số thập phân thứ hai ta được độ dài cạnh hình vuông cần tính là cm.
b) Uớc lượng số liệu với độ chính xác nên phải làm tròn số đến hàng nghìn.
Số dân thành phố uớc tính là người.

\(a.5,3.4,7+\left(-17\right).5,3-5,9\)
\(=5,3.\left[4,7+\left(-17\right)\right]-5,9\)
\(=5,3.\left(-12,3\right)-5,9\)
\(=-65,19-5,9=-71,09\)
\(b.\dfrac{2}{3}+\dfrac{-1}{3}+\dfrac{7}{15}=\dfrac{10}{15}+\dfrac{-5}{15}+\dfrac{7}{15}=\dfrac{12}{15}=\dfrac{4}{5}\)
giá trị của biểu thức \(\dfrac{1}{3}.\sqrt{\dfrac{9}{25}}-\left(\dfrac{1}{3}+\dfrac{1}{2}\right)^2\)

\(=\dfrac{1}{3}.\dfrac{3}{5}-\left(\dfrac{5}{6}\right)^2\\ =\dfrac{1}{5}-\dfrac{25}{36}\\ =-\dfrac{89}{180}\)

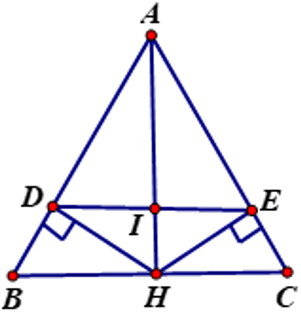
a) xét ΔABH và ΔACH, ta có :
AB = AC (giả thiết)
\(\widehat{ABC}=\widehat{ACB}\) (vì AB = AC => đó là tam giác cân, mà tam giác cân thì có 2 góc ở đáy bằng nhau)
AH là cạnh chung
ð ΔABH = ΔACH (c.c.c)
b) vì ΔABH = ΔACH, nên :
=> HB = HC (2 cạnh tương ứng)
c) hơi khó nha !

( \(\dfrac{1}{125}\) - \(x^3\) ) ( \(x^2\) + 22.66) = 0
\(\left[{}\begin{matrix}\dfrac{1}{125}-x^3=0\\x^2-2^2.6^6=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x^3=\dfrac{1}{125}\\x^2=2^2(6^3)^2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{1}{5}\\x^2=(2.6^3)^2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=432^2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=432\\x=-432\end{matrix}\right.\)
\(x\) ϵ { -432; \(\dfrac{1}{5}\); 432; }


\(\dfrac{19}{8}\times\dfrac{16}{9}+\dfrac{19}{8}\times\dfrac{2}{9}-\dfrac{19}{8}\)
= \(\dfrac{19}{8}\times\left(\dfrac{16}{9}+\dfrac{2}{9}-1\right)\)
= \(\dfrac{19}{8}\times\left(\dfrac{16+2}{9}-1\right)\)
= \(\dfrac{19}{8}\times\left(2-1\right)\)
= \(\dfrac{19}{8}\)

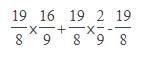
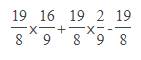
25x+2022−3x+∣−2022∣=2x+1011
�+20225−�+20223−�+20222=05x+2022−3x+2022−2x+2022=0
(15−13−12)(�+2022)=0(51−31−21)(x+2022)=0
(�+2022)=0(x+2022)=0