P= (\(\dfrac{2}{\sqrt{x}-1}\)-\(\dfrac{5}{x+\sqrt{x}-2}\)):(1+\(\dfrac{3-x}{\left(\sqrt{x}-1\right).\left(\sqrt{x}+2\right)}\)
a) rút gọn bt (làm mỗi ý này thôi cũng đc ạ)
b) Tính P khi x=6-2\(\sqrt{5}\)
c) Tìm giá trị của x để P= \(\dfrac{1}{\sqrt{x}}\)
d) Tìm x thuộc Z để P thuộc Z
e) Tìm x để P< 1-\(\sqrt{x}\)
g) Tìm min P


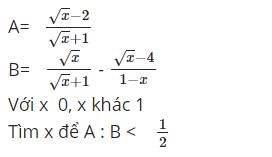 tính giá trị của A khi x= 6 -2
tính giá trị của A khi x= 6 -2