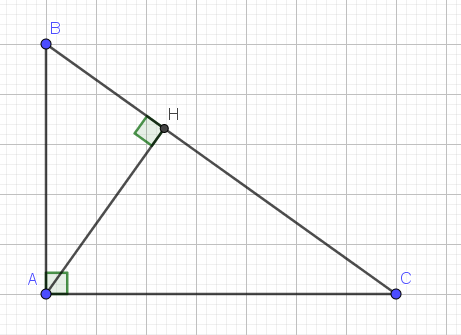
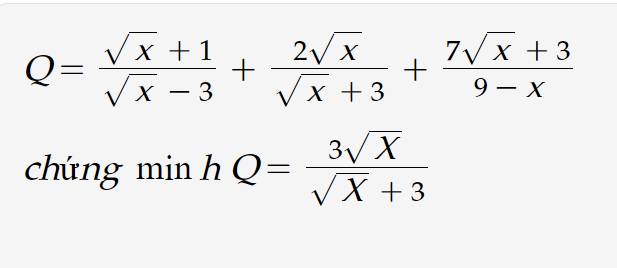cho tam giác ABC vuông tại A dường cao AH có AB=5cm,AC=12cm. a)tính ah,số do góc C.b)đg phân giác BD.kẻ tia Bx vuông gcs vs BD,tia Bx cắt AC tại E.CM rằng AD.EC=DC.AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$BC=BH+HC=61+84=145$ (cm)
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=61.84=5124$
Áp dụng định lý Pitago cho tam giác vuông $ABH, ACH$:
$AB=\sqrt{AH^2+BH^2}=\sqrt{5124+61^2}\approx 94$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{5124+84^2}\approx 110,4$ (cm)
$\cos B =\frac{AB}{BC}=\frac{94}{145}\Rightarrow \widehat{B}\approx 50^0$
$\widehat{C}=90^0-\widehat{B}\approx 90^0-50^0=40^0$

Lời giải:
ĐKXĐ: $x\geq 0 ; x\neq 9$
\(Q=\frac{(\sqrt{x}+1)(\sqrt{x}+3)+2\sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{7\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}+3)}\)
\(=\frac{x+4\sqrt{x}+3+2x-6\sqrt{x}}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{7\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}+3)}\)
$=\frac{3x-2\sqrt{x}+3-7\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)}$
$=\frac{3x-9\sqrt{x}}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{3\sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{3\sqrt{x}}{\sqrt{x}+3}$
Ta có đpcm.

\(B=\dfrac{2010}{4x+20\sqrt{x}+30}\)
\(B=\dfrac{2010}{\left(2\sqrt{x}\right)^2+2\cdot2\sqrt{x}\cdot5+25+5}\)
\(B=\dfrac{2010}{\left(2\sqrt{x}+5\right)^2+5}\)
Ta có: \(\left(2\sqrt{x}+5\right)^2+5\ge5\)
\(\Rightarrow B=\dfrac{2010}{\left(2\sqrt{x}+5\right)^2+5}\le\dfrac{2010}{5}=402\)
Vậy: \(B_{min}=402\)

Ta có
\(DG\perp AB\left(gt\right)\Rightarrow\widehat{BGD}=90^o\)
\(DF\perp BC\left(gt\right)\Rightarrow\widehat{BFD}=90^o\)
=> G và F cùng nhìn BD dưới 1 góc vuông => BGDF là tứ giác nội tiếp
\(\Rightarrow\widehat{DGF}=\widehat{DBF}\) (góc nội tiếp cùng chắn cung DF) (1)
Ta có
\(BD\perp AC\left(gt\right)\Rightarrow\widehat{BDC}=90^o\)
\(CE\perp AB\left(gt\right)\Rightarrow\widehat{BEC}=90^o\)
=> E và D cùng nhìn BC dưới 1 góc vuông => BEDC là tứ giác nội tiếp
\(\Rightarrow\widehat{DBF}=\widehat{DEC}\) (góc nội tiếp cùng chắn cung DC) (2)
Ta có
GD//CE (cùng vg với AB) \(\Rightarrow\widehat{EDG}=\widehat{DEC}\) (góc sole trong) (3)
Từ (1) (2) và (3) \(\Rightarrow\widehat{DGF}=\widehat{EDG}\) => tg IDG cân tại I
=> IG=ID (4)
Ta có
\(\widehat{DGF}+\widehat{EGF}=\widehat{DGE}=90^o\)
\(\widehat{DEC}+\widehat{DEG}=\widehat{CEG}=90^o\)
Mà từ (1) và (2) \(\Rightarrow\widehat{DGF}=\widehat{DEC}\)
\(\Rightarrow\widehat{EGF}=\widehat{DEG}\) => tg IGE cân tại I => IG=IE (5)
Từ (4) và (5) => ID=IE


Lời giải:
Trừ 2 PT theo vế ta có:
$x^2y-xy^2=y^2-x^2$
$\Leftrightarrow x^2y-xy^2+x^2-y^2=0$
$\Leftrightarrow xy(x-y)+(x-y)(x+y)=0$
$\Leftrightarrow (x-y)(xy+x+y)=0$
$\Rightarrow x-y=0$ hoặc $xy+x+y=0$
Nếu $x-y=0\Leftrightarrow x=y$. Thay vào PT(1):
$x^3+2=x^2$
$\Leftrightarrow (x+1)(x^2-2x+2)=0$
$\Leftrightarrow (x+1)[(x-1)^2+1]=0$
Hiển nhiên $(x-1)^2+1>0$ nên $x+1=0$
$\Leftrightarrow x=-1$. Vậy $(x,y)=(-1,-1)$
Nếu $xy+x+y=0$
$\Leftrightarrow xy=-(x+y)$. Thay vào pt(1):
$x(-x-y)+2=y^2$
$\Leftrightarrow 2=x^2+xy+y^2=(x+y)^2-xy=(x+y)^2+(x+y)$
$\Leftrightarrow (x+y)^2+(x+y)-2=0$
$\Leftrightarrow (x+y-1)(x+y+2)=0$
$\Rightarrow x+y=1$ hoặc $x+y=-2$
Nếu $x+y=1$ thì $xy=-1$. Theo định lý Viet thì $x,y$ là nghiệm của $T^2-T-1=0$
$\Rightarrow (x,y)=(\frac{1+\sqrt{5}}{2}, \frac{1-\sqrt{5}}{2})$ và hoán vị
Nếu $x+y=-2$ thì $xy=2$. Theo định lý Viet thì $x,y$ là nghiệm của pt $T^2+2T+2=0$
Hiển nhiên pt này vô nghiệm nên loại
Vậy...........