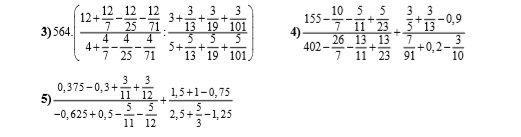
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề:
`x^2 + x + x + 1`
`= (x^2 + x) + (x+1) `
`= x(x+1) + (x+1) `
`= (x+1)(x+1)`
`x^4 +x + x + 1`
`= (x^4 + x) + (x+1) `
`= x(x^3 + 1) + (x+1) `
`= x(x+1)(x^2 - x +1) + (x+1) `
`= (x+1) (x^3 - x^2 + x) + (x+1) `
`= (x+1) (x^3 - x^2 + x+1) `

a: \(\dfrac{3x+5}{2}-x>=1+\dfrac{x+2}{3}\)
=>\(\dfrac{3x+5-2x}{2}>=\dfrac{3+x+2}{3}\)
=>\(\dfrac{x+5}{2}-\dfrac{x+5}{3}>=0\)
=>\(\dfrac{3\left(x+5\right)-2\left(x+5\right)}{6}>=0\)
=>\(\dfrac{x+5}{6}>=0\)
=>x+5>=0
=>x>=-5
b: \(\dfrac{x-2}{3}-x-2< =\dfrac{x-17}{2}\)
=>\(\dfrac{2\left(x-2\right)}{6}+\dfrac{6\left(-x-2\right)}{6}< =\dfrac{3\left(x-17\right)}{6}\)
=>\(2\left(x-2\right)+6\left(-x-2\right)< =3\left(x-17\right)\)
=>\(2x-4-6x-12< =3x-51\)
=>-4x-16<=3x-51
=>-7x<=-35
=>x>=5
c: \(\dfrac{2x+1}{3}-\dfrac{x-4}{4}< =\dfrac{3x+1}{6}-\dfrac{x-4}{12}\)
=>\(\dfrac{4\left(2x+1\right)-3\left(x-4\right)}{12}< =\dfrac{2\left(3x+1\right)-x+4}{12}\)
=>4(2x+1)-3(x-4)<=2(3x+1)-x+4
=>8x+4-3x+12<=6x+2-x+4
=>5x+16<=5x+6
=>16<=6(sai)
Vậy: BPT vô nghiệm

a: \(\dfrac{3\left(2x+1\right)}{20}+1>\dfrac{3x+52}{10}\)
=>\(\dfrac{6x+3}{20}+\dfrac{20}{20}>\dfrac{6x+104}{20}\)
=>6x+23>6x+104
=>23>104(sai)
vậy: \(x\in\varnothing\)
b: \(\dfrac{4x-1}{2}+\dfrac{6x-19}{6}< =\dfrac{9x-11}{3}\)
=>\(\dfrac{3\left(4x-1\right)+6x-19}{6}< =\dfrac{2\left(9x-11\right)}{6}\)
=>12x-3+6x-19<=18x-22
=>-22<=-22(luôn đúng)
Vậy: \(x\in R\)


1: \(\left(\dfrac{1,5+1-0,75}{2,5+\dfrac{5}{3}-1,25}+\dfrac{0,375-0,3+\dfrac{3}{11}+\dfrac{3}{12}}{-0,625+0,5-\dfrac{5}{11}-\dfrac{5}{12}}\right):\dfrac{1890}{2005}+115\)
\(=\left(\dfrac{3\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}{5\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}+\dfrac{3\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}{-5\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}\right)\cdot\dfrac{2005}{1890}+115\)
\(=0\cdot\dfrac{2005}{1890}+115=115\)
2: \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{0,6-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-0,16-\dfrac{4}{125}-\dfrac{4}{625}}\)
\(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}=1\)

Nó còn tùy từng trường hợp cụ thể của đề bài chứ em?
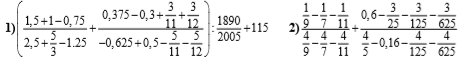

3: \(564\left(\dfrac{12+\dfrac{12}{7}-\dfrac{12}{25}-\dfrac{12}{71}}{4+\dfrac{4}{7}-\dfrac{4}{25}-\dfrac{4}{71}}:\dfrac{3+\dfrac{3}{13}+\dfrac{3}{19}+\dfrac{3}{101}}{5+\dfrac{5}{13}+\dfrac{5}{19}+\dfrac{5}{101}}\right)\)
\(=564\left(\dfrac{12\left(1+\dfrac{1}{7}-\dfrac{1}{25}-\dfrac{1}{71}\right)}{4\left(1+\dfrac{1}{7}-\dfrac{1}{25}-\dfrac{1}{71}\right)}:\dfrac{3\left(1+\dfrac{1}{13}+\dfrac{1}{19}+\dfrac{1}{101}\right)}{5\left(1+\dfrac{1}{13}+\dfrac{1}{19}+\dfrac{1}{101}\right)}\right)\)
\(=564:\left(3\cdot\dfrac{5}{3}\right)=564\cdot5=2820\)
4: \(\dfrac{155-\dfrac{10}{7}-\dfrac{5}{11}+\dfrac{5}{23}}{402-\dfrac{26}{7}-\dfrac{13}{11}+\dfrac{13}{23}}+\dfrac{\dfrac{3}{5}+\dfrac{3}{13}-0,9}{\dfrac{7}{91}+0,2-\dfrac{3}{10}}\)
\(=\dfrac{5\left(31-\dfrac{2}{7}-\dfrac{1}{11}+\dfrac{1}{23}\right)}{13\left(31-\dfrac{2}{7}-\dfrac{1}{11}+\dfrac{1}{23}\right)}+\dfrac{\dfrac{3}{5}+\dfrac{3}{13}-\dfrac{9}{10}}{\dfrac{1}{13}+\dfrac{1}{5}-\dfrac{1}{10}}\)
\(=\dfrac{5}{13}+\dfrac{3\left(\dfrac{1}{5}+\dfrac{1}{13}-\dfrac{1}{10}\right)}{\dfrac{1}{5}+\dfrac{1}{13}-\dfrac{1}{10}}=\dfrac{5}{13}+3=\dfrac{44}{13}\)
5: \(\dfrac{0,375-0,3+\dfrac{3}{11}+\dfrac{3}{12}}{-0,625+0,5-\dfrac{5}{11}-\dfrac{5}{12}}+\dfrac{1,5+1-0,75}{2,5+\dfrac{5}{3}-1,25}\)
\(=-\dfrac{\dfrac{3}{8}-\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}}{\dfrac{5}{8}-\dfrac{5}{10}+\dfrac{5}{11}+\dfrac{5}{12}}+\dfrac{\dfrac{3}{2}+\dfrac{3}{3}-\dfrac{3}{4}}{\dfrac{5}{2}+\dfrac{5}{3}-\dfrac{5}{4}}\)
\(=-\dfrac{3\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}{5\left(\dfrac{1}{8}-\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)}+\dfrac{3\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}{5\left(\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}\right)}\)
\(=-\dfrac{3}{5}+\dfrac{3}{5}=0\)