a)Áp suất ở dưới pittong nhỏ là: \(\dfrac{10m_2}{S_2}=\dfrac{10m_1}{S_1}+10D\cdot h\)

\(\Rightarrow\dfrac{10m_2}{25\cdot10^{-4}}=\dfrac{10\cdot1}{50\cdot10^{-4}}+10\cdot1000\cdot0,1\Rightarrow m_2=0,75kg=750g\)

b)Khi đặt lên pittong bên trái một lượng \(m=300g=0,3kg\) thì nó di chuyển xuống dưới một đoạn:

\(\dfrac{10\left(m_2+m\right)}{S_2}=\dfrac{10m_1}{S_1}+10D\cdot\Delta h\)

\(\Rightarrow\dfrac{10\cdot\left(0,75+0,3\right)}{25\cdot10^{-4}}=\dfrac{10\cdot1}{50\cdot10^{-4}}+10\cdot1000\cdot\Delta h\)

\(\Rightarrow\Delta h=0,22m=22cm\)

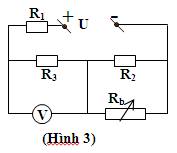
CTM: \((R_1nt(R_3//R_4))//R_2\)

\(R_{34}=\dfrac{R_3\cdot R_4}{R_3+R_4}=\dfrac{6\cdot2}{6+2}=\dfrac{3}{2}\Omega\)

\(R_{134}=R_1+R_{34}=6+1,5=7,5\Omega\)

\(R_{tđ}=\dfrac{R_{134}\cdot R_2}{R_{134}+R_2}=\dfrac{7,5\cdot6}{7,5+6}=\dfrac{10}{3}\Omega\)

\(I_{34}=I_{134}=\dfrac{U_{134}}{R_{134}}=\dfrac{U_{AB}}{R_{134}}=\dfrac{18}{7,5}=2,4A\)

\(U_3=U_4=U_{34}=I_{34}\cdot R_{34}=2,4\cdot1,5=3,6V\)

\(I_A=I_3=\dfrac{U_3}{R_3}=\dfrac{3,6}{6}=0,6A\)

a) Để x + 4 là số nguyên dương nhỏ nhất thì:

x + 4 = 1

⇒ x = 1 - 4

⇒ x = -3 

b) Để 2x + 5 là số nguyên âm nhỏ có 2 chữ số thì:

2x + 5 = -99 

⇒ 2x = -99 - 5

⇒ 2x = -104 

⇒ x = -104 : 2

⇒ x = -52 

c) Để 2023 - x là số nguyên âm lớn nhất thì:

2023 - x = -1

⇒ x = 2023 + 1

⇒ x = 2024 

d) Để 3x + 5 là số nguyê âm lớn nhất có 3 chữ số thì:

3x + 5 = -100 

⇒ 3x = -100 - 5

⇒ 3x = -105

⇒ x = -105 : 3

⇒ x = -35

Đặt đúng môn học Toán bạn nhé. -

\(1mm=1.10^{-3}m\\ S=\dfrac{d^2\pi}{4}=\dfrac{\left(1.10^{-3}\right)^2.3,14}{4}=7,85.10^{-7}\\ R=\rho\cdot\dfrac{l}{S}=0,4.10^{-6}\cdot\dfrac{4}{7,85.10^{-7}}\approx2,04\Omega\)

\(A=4\cdot4^2\cdot4^3\cdot4^4\cdot4^5\cdot...\cdot4^{198}\cdot4^{199}\cdot4^{200}\)

    \(=4^{1+2+3+4+5+...+198+199+200}\)

Đặt \(B=1+2+3+4+5+...+198+199+200\)

Số số hạng của B là: \(N=\left(200-1\right):1+1=200\left(số\right)\)

Tổng \(B=\dfrac{\left(200+1\right)\cdot200}{2}=20100\)

Vậy \(A=4^{20100}\)