giai giupe em
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b) \(\left(x+3\right)^2-5x-15=0\\ \Leftrightarrow\left(x+3\right)^2-5\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x+3-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+3=0\\x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là : \(S=\left\{-3;2\right\}\)
c) \(2x^5-4x^3+2x=0\\ \Leftrightarrow2x\left(x^4-2x^2+1\right)=0\\ \Leftrightarrow2x\left(x^2-1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\\left(x^2-1\right)^2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Vậy tập nghiệm của pt là : \(S=\left\{0;1;-1\right\}\)

a) 2x(x² - xy³)
= 2x.x² - 2x.xy³
= 2x³ - 2x²y³
b) (12x³y⁵ - 21x⁴y²) : 3x²y²
= 12x³y⁵ : 3x²y² - 21x⁴y² : 3x²y²
= 4xy³ - 7x²
a, 2\(x\).(\(x^2\) - \(xy^3\))
= 2\(x^3\) - 2\(x^2\)y3
b, (12\(x^3\)y5 - 21\(x^4\)y2) :(3\(x^2\)y2)
= 3\(x^2\).y2.(4\(xy^3\) - 7\(x^2\))
= 4\(xy^3\) - 7\(x^2\)

a) 2x2- 6x2
= -4x2
b) x2-6x+9-y2
= (x-3)2 -y2
= (x-3-y).(x-3+y)

Lời giải:
Ta có:
$a^3+b^3=(a+b)(a^2-ab+b^2)=(a+b)[(a^2+ab+b^2)-2ab]$
Áp dụng BĐT AM-GM:
$a^2+ab+b^2=(a^2+b^2)+ab\geq 2ab+ab=3ab$
$\Rightarrow 2ab\leq \frac{2(a^2+ab+b^2)}{3}$
$\Rightarrow a^2-ab+b^2=a^2+b^2+ab-2ab\geq a^2+b^2+ab- \frac{2}{3}(a^2+ab+b^2)=\frac{1}{3}(a^2+ab+b^2)$
$\Rightarrow a^3+b^3=(a+b)(a^2-ab+b^2)\geq \frac{1}{3}(a+b)(a^2+ab+b^2)$
$\Rightarrow \frac{a^3+b^3}{a^2+ab+b^2}\geq \frac{1}{3}(a+b)$
Hoàn toàn tương tự với các phân thức khác và cộng theo vế thu được:
$P\geq \frac{1}{3}(a+b)+\frac{1}{3}(b+c)+\frac{1}{3}(c+a)=\frac{2}{3}(a+b+c)$
$\geq \frac{2}{3}.3\sqrt[3]{abc}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $a=b=c=1$
Lời giải:
Ta có:
$a^3+b^3=(a+b)(a^2-ab+b^2)=(a+b)[(a^2+ab+b^2)-2ab]$
Áp dụng BĐT AM-GM:
$a^2+ab+b^2=(a^2+b^2)+ab\geq 2ab+ab=3ab$
$\Rightarrow 2ab\leq \frac{2(a^2+ab+b^2)}{3}$
$\Rightarrow a^2-ab+b^2=a^2+b^2+ab-2ab\geq a^2+b^2+ab- \frac{2}{3}(a^2+ab+b^2)=\frac{1}{3}(a^2+ab+b^2)$
$\Rightarrow a^3+b^3=(a+b)(a^2-ab+b^2)\geq \frac{1}{3}(a+b)(a^2+ab+b^2)$
$\Rightarrow \frac{a^3+b^3}{a^2+ab+b^2}\geq \frac{1}{3}(a+b)$
Hoàn toàn tương tự với các phân thức khác và cộng theo vế thu được:
$P\geq \frac{1}{3}(a+b)+\frac{1}{3}(b+c)+\frac{1}{3}(c+a)=\frac{2}{3}(a+b+c)$
$\geq \frac{2}{3}.3\sqrt[3]{abc}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $a=b=c=1$

Bài 2
a) A = (-2x²y² + 4xy - 6xy³) : 2xy
= -xy + 2 - 3y²
Thay x = 1/2; y = 4 vào A, ta có:
A = -1/2 . 4 + 2 - 3 . 2²
= -2 + 2 - 12
= -12
b) B = 25x² - 10xy² + y⁴
= (5x - y²)²
Thay x = 2; y = 3 vào B, ta có:
B = (5.2 - 3²)²
= (10 - 9)²
= 1²
= 1
c) C = (3x + 2)² + 2(3x + 2)(2y - 1)² + (2y - 1)²
= (3x + 2 + 2y - 1)²
= (3x + 2y + 1)²
Thay x = 1/3; y = -1/2 vào C, ta có:
C = [3 . 1/3 + 2 . (-1/2) + 1]²
= (1 - 1 + 1)²
= 1²
= 1
Bài 3
a) x³ + 2x² = x²(x + 2)
b) 3(x - y) - 5x(y - x)
= 3(x - y) + 5x(x - y)
= (x - y)(3 + 5x)
c) 4x³ - 9x
= x(4x² - 9)
= x(2x - 3)(2x + 3)
d) (x - 2y)² - 4(x + y)²
= (x - 2y)² - [2(x + y)]²
= (x - 2y) - (2x + 2y)²
= (x - 2y - 2x - 2y)(x - 2y + 2x + 2y)
= (-x - 4y).3x
= -3x(x + 4y)
e) x²y + x² - 4y - 4
= (x²y + x²) - (4y + 4)
= x²(y + 1) - 4(y + 1)
= (y + 1)(x² - 4)
= (y + 1)(x - 2)(x + 2)
f) -27x³(x + 1) + x + 1
= - 27x³(x + 1) + (x + 1)
= (x + 1)(-27x³ + 1)
= (x + 1)(1 - 27x³)
= (x + 1)(1 - 3x)(1 + 3x + 9x²)

b, 9a2 - 6a + 1 - 25b2
= (3a - 1)2 - (5b)2
= (3a - 1 - 5b).(3a -1 + 5b)

b,
B = \(\dfrac{1}{x+2}\) + \(\dfrac{5}{x-2}\) - \(\dfrac{2x}{x^2-4}\) (đk \(x\) ≠ -2; 2)
B = \(\dfrac{1}{x+2}+\dfrac{5}{x-2}-\dfrac{2x}{\left(x-2\right)\left(x+2\right)}\)
B = \(\dfrac{x-2+5.\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\) - \(\dfrac{2x}{\left(x-2\right)\left(x+2\right)}\)
B = \(\dfrac{x-2+5x+10-2x}{\left(x+2\right).\left(x-2\right)}\)
B = \(\dfrac{4x+8}{\left(x-2\right)\left(x+2\right)}\)
B = \(\dfrac{4}{x-2}\)
C,
C = \(\dfrac{1}{x+1}\) + \(\dfrac{2}{1-x}\) - \(\dfrac{1-5x}{x^2-1}\) Đk \(x\ne\) -1; 1
C = \(\dfrac{x-1}{\left(x+1\right)\left(x-1\right)}\) - \(\dfrac{2.\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\) - \(\dfrac{1-5x}{\left(x-1\right)\left(x+1\right)}\)
C = \(\dfrac{x-1-2x-2-1+5x}{\left(x-1\right)\left(x+1\right)}\)
C = \(\dfrac{-4x-4}{\left(x+1\right)\left(x-1\right)}\)
C = \(\dfrac{-4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
C = \(\dfrac{-4}{x-1}\)


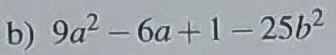

đề đâu ạ?