giúp mình vs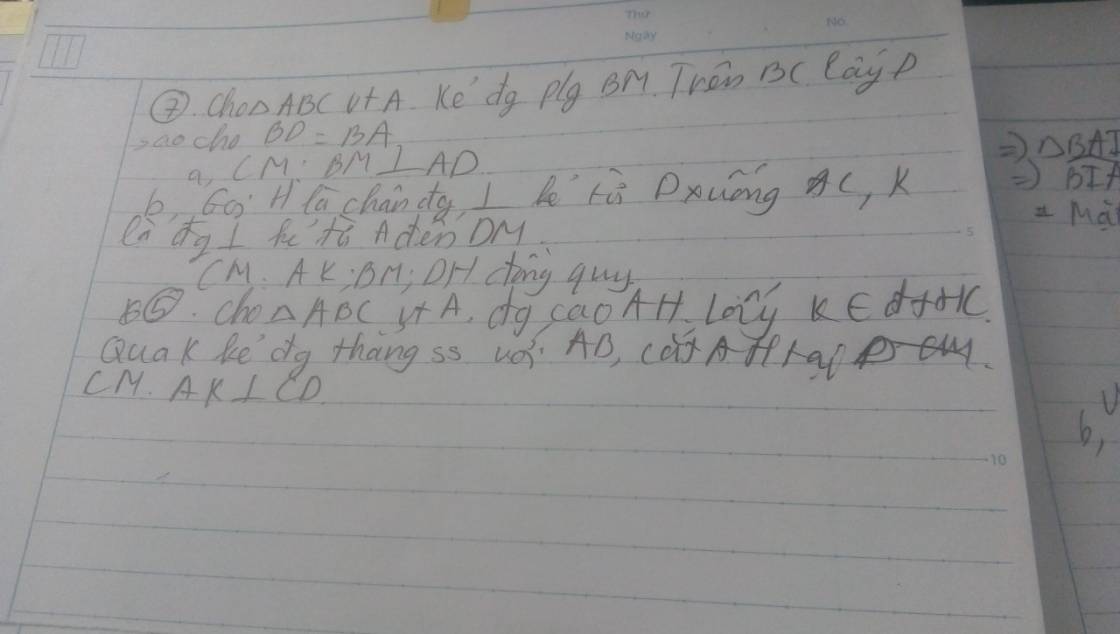
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

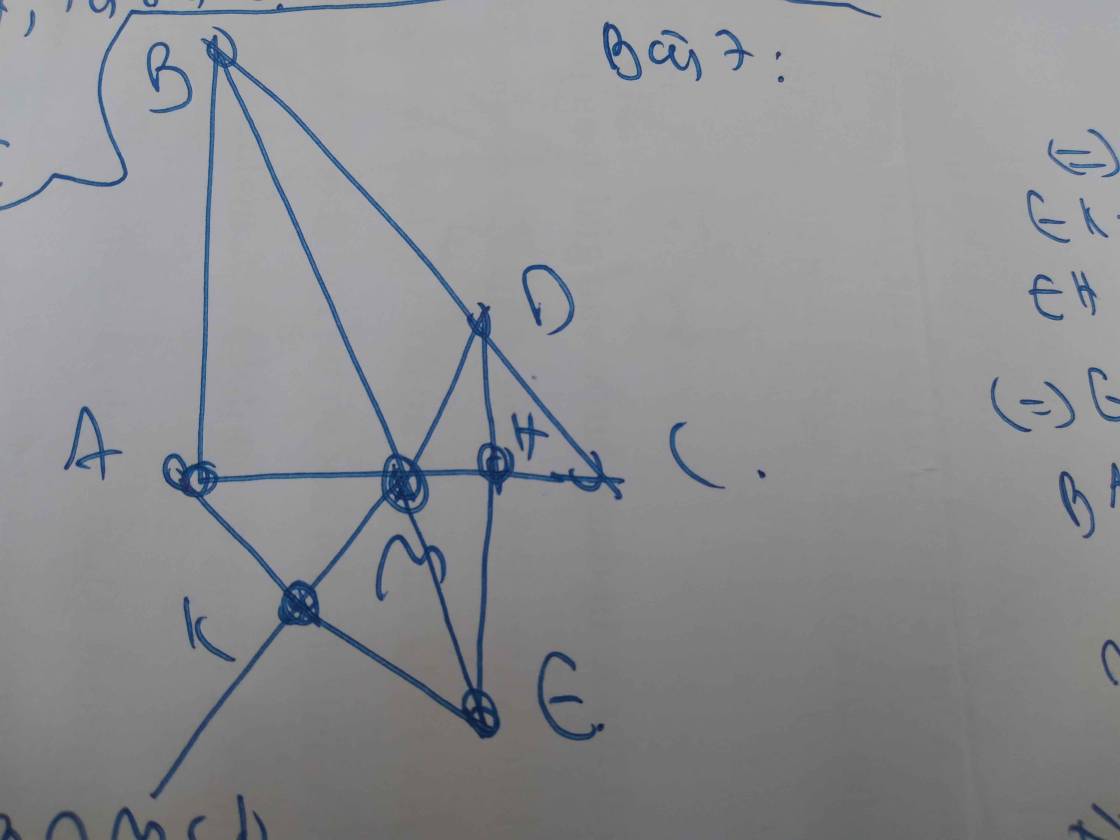
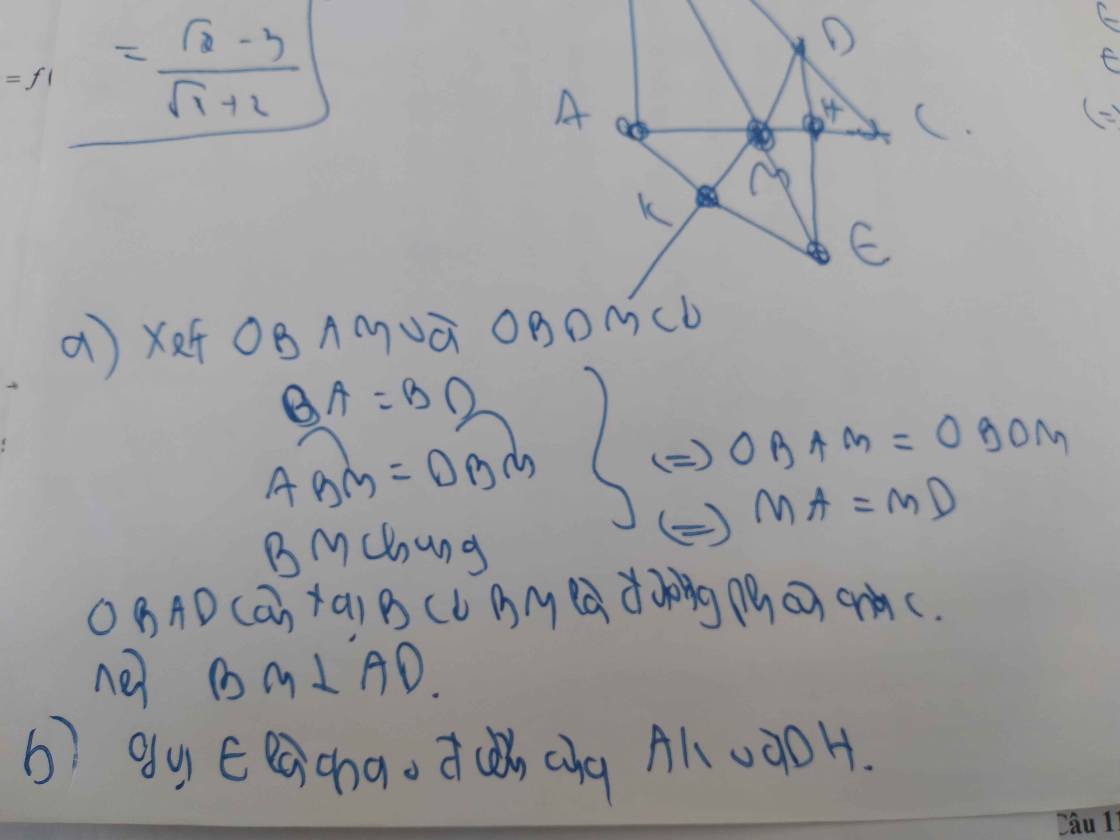

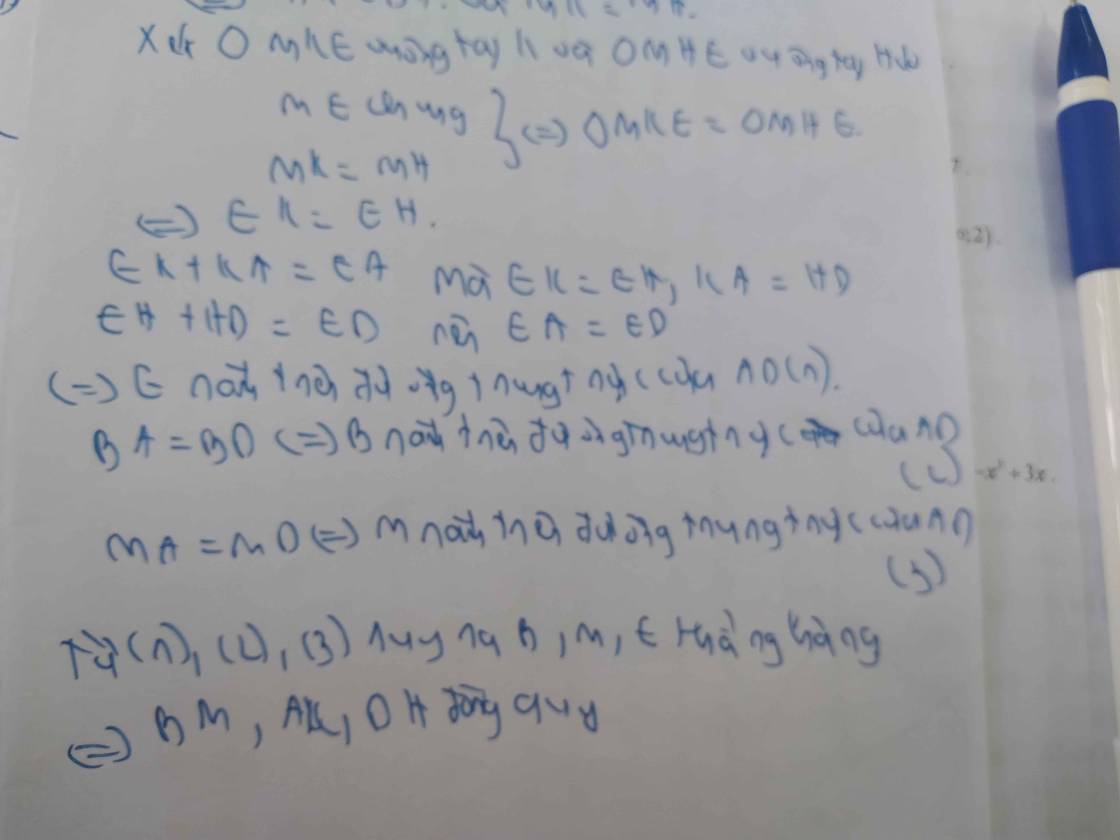

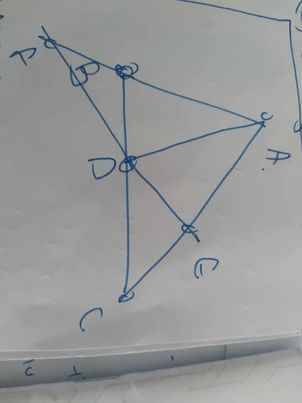
=>BD=DE
=>D nằm trên đường trung trực của BE(1)
Ta có: AB=AE
=>A nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra AD là đường trung trực của BE
=>AD\(\perp\)BE
b: Ta có: ΔABD=ΔAED
=>\(\widehat{ABD}=\widehat{AED}\)
mà \(\widehat{ABD}+\widehat{DBF}=180^0\)(hai góc kề bù)
và \(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
nên \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDBF=ΔDEC
d: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
mà AB<AC
nên BD<CD
a) Do AE = AB và AD là tia phân giác của góc BAC nên tam giác ABD = tam giác AED (theo định lý cạnh góc cạnh).
Từ đó, suy ra AD vuông góc với BE (do hai tam giác cân tại D).
b) Do tam giác ABD = tam giác AED nên góc BAD = góc EAD.
Lại có góc BAF = góc EAD (cùng chắn cung BE).
Suy ra tam giác BAF = tam giác EAD (theo định lý góc cạnh góc).
Do đó, tam giác BDF = tam giác EDC.
c) Để chứng minh AI vuông góc BC, cần phải xác định rõ vị trí của điểm I. Nếu I là trung điểm của BD thì AI sẽ vuông góc với BC.
d) Do AB < AC và tam giác ABD = tam giác AED nên BD < DC.

Gọi A là biến cố "quả bóng lấy ra là số nguyên tố"
=>A={5}
=>n(A)=1
\(P\left(A\right)=\dfrac{1}{5}\)
Gọi B là biến cố "Quả bóng lấy ra ghi số chia hết cho 5"
=>B={5;10;15;20;25}
=>n(B)=5
\(P\left(B\right)=\dfrac{5}{5}=1\)
Gọi C là biến cố "Quả bóng lấy ra ghi số chia hết cho 6"
=>C=\(\varnothing\)
=>\(P\left(C\right)=0\)
a: Biến cố chắc chắn là biến cố B
b: \(P\left(A\right)=\dfrac{1}{5}\)

Hình bạn tự vẽ nhé
a,Xét tam giác BAD và tam giác EDA:
AD chung
ABD=AED=90 độ( tam giác ABC vuông tại B, DE vuông góc AC)
BAD=CAD(AD là tia phân giác)
Suy ra tam giác BAD= tam giác EDA(cạnh huyền - góc nhọn)
b, Vì tam giác BAD= tam giác EDA (cmt)
Suy ra: AB=AE(2 cạnh tương ứng)
Suy ra A thuộc trung trực BE 1
Vì tam giác BAD = tam giác EDA(CMA)
Suy ra:BD=DE
Suy ra: D thuộc trung trực BE 2
Từ 1 và 2
Suy ra AD là đường trung trực BE
c,AB=AE(cmt) 3
BK=EC(gt) 4
AB+BK=AK 5
AE+EC=AC 6
Từ 3,4,5,6
Suya ra AK =AC
Suy ra tam giác AKC cân tại A 7
Mà AD là tia phân giác 8
Từ 7 và 8
Suy ra AD là đg cao tam giác AKC
Xét tam giác AKC có:
Đg cao CB( tam giác ABC vuông tại B)
Đg cao AD (cmt)
Mà AD cắt CB tại D
Suy ra D là trực tâm tam giác AKC 9
Suy ra KE là đg cao còn lại 10
Từ 9,10
Suy ra D thuộc KE
Suy ra K,D,E thg hàng

a, P(x) = 6x^3 - 3x^2 + 5x - 1
Q(x) = -6x^3 + 3x^2 - 2x + 7
b, P(x) + Q(x)
= ( 6x^3 - 3x^2 + 5x - 1 ) + ( -6x^3 +3x^2 - 2x +7 )
= 6x^3 - 3x^2 + 5x -1 + ( -6x^3 ) + 3x^2 - 2x +7
= [ 6x^3 + ( -6x^3) ] + (-3x^2 + 3x^2 ) + ( 5x - 2x ) + ( -1 +7 )
= 3x + 6
P(x) - Q(x)
= (6x^3 - 3x^2 + 5x - 1 ) - (-6x^3 + 3x^2 - 2x + 7 )
= 6x^3 - 3x^2 + 5x -1 - 6x^3 - 3x^2 + 2x - 7
= ( 6x^3 - 6x^3 ) + (-3x^2 - 3x^2 ) + ( 5x +2x ) + ( -1 - 7 )
= -6x^2 + 7x + ( -8)

Lời giải:
\(A=(\frac{-3}{4}x^2y^5).(4x^3y)=\frac{-3}{4}.4(x^2.x^3)(y^5.y)\\
=-3x^5y^6\)
Hệ số: $-3$
Phần biến: $x^5y^6$
Bậc: $5+6=11$
c.
Tại $x=-1$ và $y=1$ thì:
$A=-3(-1)^5.1^6=3$

`#3107.101107`
`1.`
`a)`
`A(x) = 2x^3 - 3x^2 + 2x + 1`
Bậc của đa thức: `3`
`B(x) = 3x^3 + 2x^2 - x - 6`
Bậc của đa thức: `3`
`b)`
Thay `x = 2` vào A:
`A(2) = 2 * 2^3 - 3 * 2^2 + 2 * 2 + 1`
`= 2^4 - 3 * 4 + 2^2 + 1`
`= 16 - 12 + 4 + 1 = 9`
Vậy, tại `x = 2` thì `A(2) = 9`
`c)`
`A(x) + B(x)`
`= 2x^3 - 3x^2 + 2x + 1 + 3x^3 + 2x^2 - x - 6`
`= (2x^3 + 3x^3) + (-3x^2 + 2x^2) + (2x - x) + (1 - 6)`
`= 5x^3 - x^2 + x - 5`
`A(x) - B(x)`
`= 2x^3 - 3x^2 + 2x + 1 - (3x^3 + 2x^2 - x - 6)`
`= 2x^3 - 3x^2 + 2x + 1 - 3x^3 - 2x^2 + x + 6`
`= (2x^3 - 3x^3) - (3x^2 + 2x^2) + (2x + x) + (1 + 6)`
`= -x^3 - 5x^2 + 3x + 7.`

a: Xét ΔACB có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: E nằm trên đường trung trực của AC
=>EA=EC
=>ΔEAC cân tại E
c: Ta có: \(\widehat{EAC}+\widehat{EAB}=\widehat{BAC}=90^0\)
\(\widehat{ECA}+\widehat{EBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{EAC}=\widehat{ECA}\)(ΔEAC cân tại E)
nên \(\widehat{EAB}=\widehat{EBA}\)
=>ΔEAB cân tại E
=>EA=EB
mà EA=EC
nên EB=EC
=>E là trung điểm của BC
Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>A,G,E thẳng hàng
a) So sánh các góc A, B, C:
Tam giác ABC là tam giác vuông tại A (vì BC2 = AB2 + AC2). Do đó ta có:
Góc A là góc vuông, có độ lớn là 90 độ.
Góc B nhỏ hơn góc C (vì cạnh đối diện góc B nhỏ hơn cạnh đối diện góc C).
b) Trung trực của AC cắt tại BC tại E chứng minh tam giác AEC cân:
Gọi D là trung điểm của AC. Khi đó, DE là trung trực của AC. Theo tính chất của trung trực, ta có BD = DC.
Do tam giác ABC là tam giác vuông tại A, nên BD = DC = \(\dfrac{1}{2}\)AC = 4cm.
Vì vậy, tam giác AEC là tam giác cân tại E (vì AE = EC).

\(B=2^{2016}-2^{2015}+...+2^2-2^1+1\)
=>\(2B=2^{2017}-2^{2016}+...+2^3-2^2+2\)
=>\(2B+B=2^{2017}-2^{2016}+...+2^3-2^2+2+2^{2016}-2^{2015}+...+2^2-2+1\)
=>\(3B=2^{2017}+1\)
=>\(B=\dfrac{2^{2017}+1}{3}\)
Lời giải:
$B=2^{2016}-2^{2015}+2^{2014}-2^{2013}+...+2^2-2^1+2^0$
$2B=2^{2017}-2^{2016}+2^{2015}-2^{2014}+...+2^3-2^2+2^1$
$\Rightarrow B+2B=2^{2017}+2^0=2^{2017}+1$
$\Rightarrow 3B=2^{2017}+1$
$\Rightarrow B=\frac{2^{2017}+1}{3}$
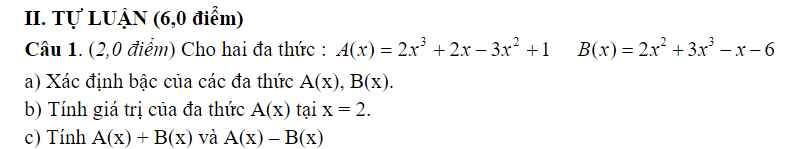




 giải theo cách hợp lí nhất nha sos!!!!!!
giải theo cách hợp lí nhất nha sos!!!!!!