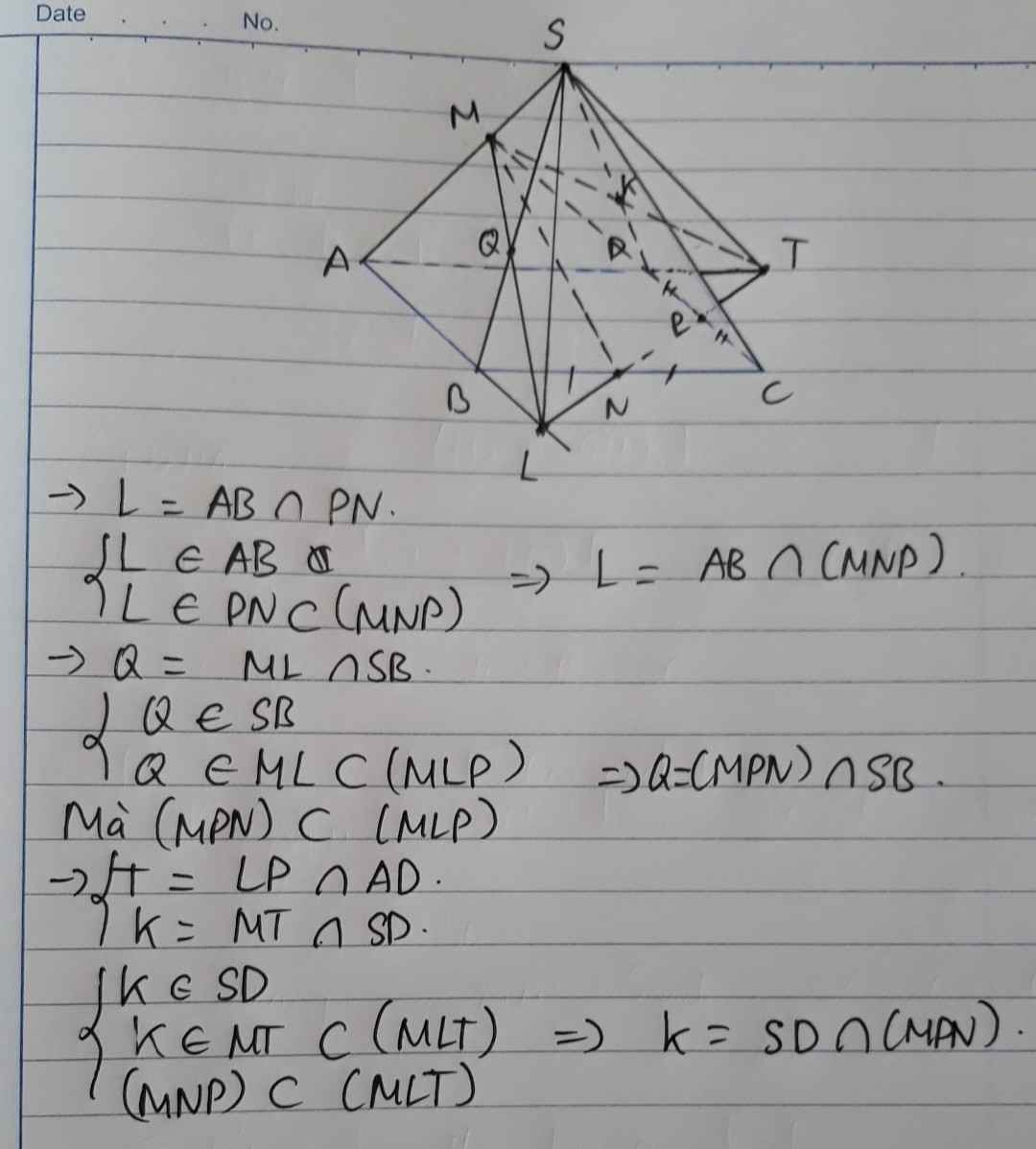
C1: Chóp SABCD có đáy ABCD là hình bình hành, M thuộc SA. Gọi N,P là trung điểm BC, CD . Tìm g/điểm của mp (MNP) với AB, SB, SD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số số hạng là \(\dfrac{\left(2x+1-3\right)}{2}+1=\dfrac{2x-2}{2}+1=x-1+1=x\left(số\right)\)
Tổng của dãy số là \(\dfrac{x\left(2x+1+3\right)}{2}=x\left(x+2\right)\)
Theo đề, ta có: x(x+2)=624
=>\(x^2+2x-624=0\)
=>(x+26)(x-24)=0
=>\(\left[{}\begin{matrix}x=-26\\x=24\end{matrix}\right.\)


1: DA=DK
=>ΔDAK cân tại D
=>\(\widehat{DAK}=\widehat{DKA}\)
mà \(\widehat{DKA}=\widehat{KAB}\)(hai góc so le trong, AB//DK)
nên \(\widehat{DAK}=\widehat{BAK}\)
=>AK là phân giác của góc BAD
2: ta có: CD=CK+KD
CD=AD+BC
Do đó: CK+KD=AD+BC
mà DA=DK
nên CK=CB
3: CK=CB
=>ΔCBK cân tại C
=>\(\widehat{CKB}=\widehat{CBK}\)
mà \(\widehat{CKB}=\widehat{ABK}\)(hai góc so le trong, AB//CK)
nên \(\widehat{ABK}=\widehat{CBK}\)
=>BK là phân giác của góc ABC

1:ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC tại H
Xét tứ giác AHCD có
O là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
2: AHCD là hình chữ nhật
=>AD//HC và AD=HC
Ta có: AD//HC
=>AD//HB
Ta có: AD=CH
mà CH=HB
nên AD=HB
Xét tứ giác ADHB có
AD//HB
AD=HB
Do đó: ADHB là hình bình hành
3: \(CH=\dfrac{CB}{2}=3\left(cm\right)\)
AHCD là hình chữ nhật
=>\(S_{AHCD}=AH\cdot HC=4\cdot3=12\left(cm^2\right)\)

a: Xét ΔBMO có \(\widehat{BMO}+\widehat{MBO}+\widehat{MOB}=180^0\)
=>\(\widehat{BMO}+\widehat{MOB}=180^0-60^0=120^0\)(1)
\(\widehat{MOB}+\widehat{MON}+\widehat{NOC}=180^0\)
=>\(\widehat{MOB}+\widehat{NOC}=180^0-60^0=120^0\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{BMO}=\widehat{CON}\)
Xét ΔBMO và ΔCON có
\(\widehat{BMO}=\widehat{CON}\)
\(\widehat{MBO}=\widehat{OCN}\left(=60^0\right)\)
Do đó: ΔBMO~ΔCON
b: ΔBMO~ΔCON
=>\(\dfrac{OM}{ON}=\dfrac{BM}{CO}=\dfrac{BM}{BO}\)
c:
\(\dfrac{OM}{ON}=\dfrac{BM}{BO}\)
=>\(\dfrac{BM}{OM}=\dfrac{BO}{ON}\)
Xét ΔBMO và ΔOMN có
\(\dfrac{BM}{OM}=\dfrac{BO}{ON}\)
\(\widehat{MBO}=\widehat{MON}\left(=60^0\right)\)
Do đó: ΔBMO~ΔOMN
=>\(\widehat{BMO}=\widehat{OMN}\)
=>MO là phân giác của góc BMN

a: \(101^2=\left(100+1\right)^2=100^2+2\cdot100\cdot1+1^2\)
=10000+200+1
=10201
b: \(64^2+36^2+72\cdot64\)
\(=64^2+2\cdot64\cdot36+36^2\)
\(=\left(64+36\right)^2=100^2=10000\)
c: \(54^2+46^2-2\cdot54\cdot46=\left(54-46\right)^2=8^2=64\)
d: \(98\cdot102=\left(100-2\right)\left(100+2\right)=100^2-4=9996\)

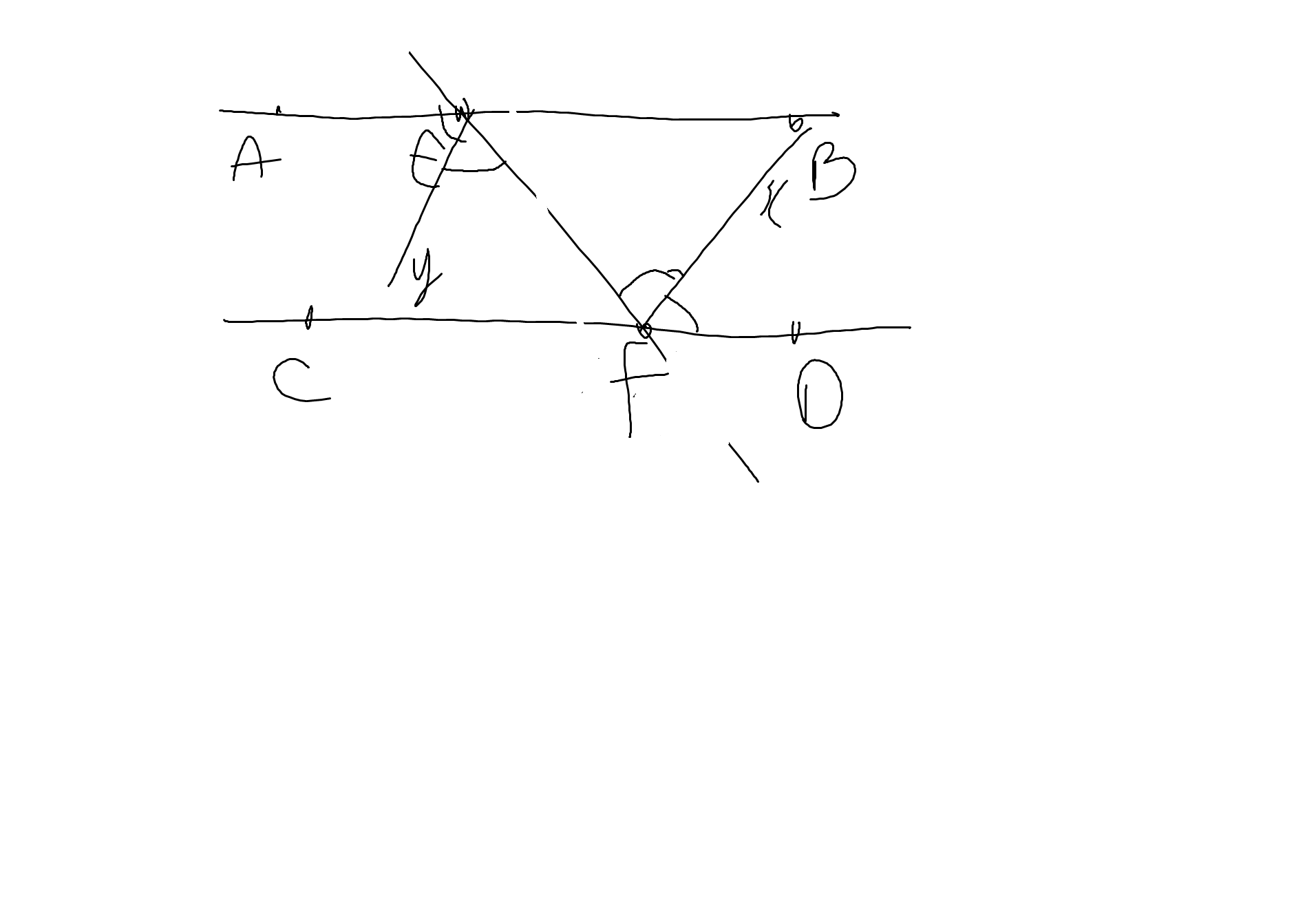
Gọi hai góc so le trong là \(\widehat{AEF};\widehat{EFD}\); Ey;Fx lần lượt là phân giác của góc AEF;góc EFD
Vì AB//CD nên \(\widehat{AEF}=\widehat{EFD}\)(hai góc so le trong)
mà \(\widehat{yEF}=\dfrac{\widehat{AEF}}{2};\widehat{xFE}=\dfrac{\widehat{EFD}}{2}\)
nên \(\widehat{yEF}=\widehat{xFE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ey//Fx