\(\sqrt{x^2+1}-x=3\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{\dfrac{45\left(x+y\right)^2.y^2}{16}}\left(dkxd:x\ge0,y\ge0\right)\\ =\dfrac{\sqrt{45\left(x+y\right)^2.y^2}}{\sqrt{16}}\\ =\dfrac{\sqrt{45}.\sqrt{\left(x+y\right)^2}.\sqrt{y^2}}{\sqrt{4^2}}\\ =\dfrac{\sqrt{3^2.5}.\left|x+y\right|.\left|y\right|}{4}\\ =\dfrac{3\sqrt{5}\left(x+y\right).y}{4}\\ =\dfrac{3\sqrt{5}\left(xy+y^2\right)}{4}\)

\(VT=\dfrac{a}{1+a^2}+\dfrac{b}{1+b^2}=\dfrac{a}{ab+a+b+a^2}+\dfrac{b}{ab+a+b+b^2}\)
\(=\dfrac{a}{\left(a+b\right).\left(a+1\right)}+\dfrac{b}{\left(a+b\right).\left(b+1\right)}\)
\(=\dfrac{\left(a+b\right).\left(ab+a+ab+b\right)}{\left(a+b\right)^2.\left(a+1\right).\left(b+1\right)}=\dfrac{ab+1}{\left(a+b\right).\left(ab+a+b+1\right)}\)
\(=\dfrac{ab+1}{2.\left(a+b\right)}\)(1)
\(VP=\dfrac{ab+1}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{ab+1}{\sqrt{2\left(a+b\right)^2.\left(a+1\right).\left(b+1\right)}}\)
\(=\dfrac{ab+1}{2\left(a+b\right)}\) (2)
Từ (1) (2) => ĐPCM
Giải
Với a,b > 0, ta có:
\(\dfrac{a}{1+a^2}+\dfrac{b}{1+b^2}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\)
Tương đương
\(\dfrac{a+ab^2+b+a^2b}{\left(1+a^2\right)\left(1+b^2\right)}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\\ \Leftrightarrow\dfrac{a+b+ab\left(a+b\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\\ \Leftrightarrow\dfrac{\left(a+b\right)\left(ab+1\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1+ab}{\sqrt{2}}\\ \Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1}{\sqrt{2}}\)
Mặt khác, \(\left(1+a^2\right)\left(1+b^2\right)=\left(a^2+a+b+ab\right)\left(b^2+a+b+ab\right)\\ =\left(a+b\right)\left(a+1\right)\left(a+b\right)\left(b+1\right)\\ =\left(a+b\right)^2\left[\left(a+1\right)\left(b+1\right)\right]\\ =\left(a+b\right)^2\left(a+b+ab+1\right)\\ =2\left(a+b\right)^2\)
Do đó phương trình đã cho tương đương:
\(\Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{2\left(a+b\right)^2}}=\dfrac{1}{\sqrt{2}}\\\Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{2}.\left(a+b\right)}=\dfrac{1}{\sqrt{2}}\left(a,b>0\right)\\ \Leftrightarrow\dfrac{1}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\left(1\right)\)
Vì phương trình (1) đúng nên phương trình ban đầu cũng đúng
Suy ra điều phải chứng minh

Ta có \(x^2+\dfrac{1}{x^2}=7\)
\(\Leftrightarrow x^2+\dfrac{1}{x^2}+2.x.\dfrac{1}{x}=9\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2=9\)
\(\Leftrightarrow x+\dfrac{1}{x}=3\) (Do x > 0) (1)
Từ (1) \(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^3=27\Leftrightarrow x^3+\dfrac{1}{x^3}+3.\left(x+\dfrac{1}{x}\right)=27\)
\(\Leftrightarrow x^3+\dfrac{1}{x^3}=18\)
Ta lại có \(\left(x+\dfrac{1}{x}\right)^5=x^5+5x^3+10x+\dfrac{10}{x}+\dfrac{5}{x^3}+\dfrac{1}{x^5}=243\)
\(\Leftrightarrow F=x^5+\dfrac{1}{x^5}=243-5.\left(\dfrac{1}{x^3}+x^3\right)-10.\left(x+\dfrac{1}{x}\right)=123\)

\(1,\sqrt{8}-3\sqrt{32}+\sqrt{72}=2\sqrt{2}-3.4\sqrt{2}+6\sqrt{2}=2\sqrt{2}-12\sqrt{2}+6\sqrt{2}=-4\sqrt{2}\)
\(2,6\sqrt{12}-2\sqrt{48}+5\sqrt{75}-7\sqrt{108}=6.2\sqrt{3}-2.4\sqrt{3}+5.5\sqrt{3}-7.6\sqrt{3}=12\sqrt{3}-8\sqrt{3}+25\sqrt{3}-42\sqrt{3}=-13\sqrt{3}\)
\(3,-\sqrt{20}+3\sqrt{45}-6\sqrt{80}-\dfrac{1}{5}\sqrt{125}\\ =-2\sqrt{5}+3.3\sqrt{5}-6.4\sqrt{5}-\dfrac{1}{5}.5\sqrt{5}\\ =-2\sqrt{5}+9\sqrt{5}-24\sqrt{5}-\sqrt{5}\\ =-18\sqrt{5}\)
\(4,2\sqrt{5}-\sqrt{125}-\sqrt{80}=2\sqrt{5}-5\sqrt{5}-4\sqrt{5}=\sqrt{5}\left(2-5-4\right)=-7\sqrt{5}\)
\(5,3\sqrt{2}-\sqrt{8}+\sqrt{50}-4\sqrt{32}=3\sqrt{2}-2\sqrt{2}+5\sqrt{2}-16\sqrt{2}=\sqrt{2}\left(3-2+5-16\right)=-10\sqrt{2}\)
\(6,\sqrt{27}-2\sqrt{3}+2\sqrt{48}-3\sqrt{75}\\ =\sqrt{3^2.3}-2\sqrt{3}+2\sqrt{4^2.3}-3\sqrt{5^2.3}\\ =3\sqrt{3}-2\sqrt{3}+8\sqrt{3}-15\sqrt{3}\\ =\sqrt{3}\left(3-2+8-15\right)\\ =-6\sqrt{3}\)
\(7,3\sqrt{2}-4\sqrt{18}+\sqrt{32}-\sqrt{50}\\ =3\sqrt{2}-4.3\sqrt{2}+4\sqrt{2}-5\sqrt{2}\\ =3\sqrt{2}-12\sqrt{2}+4\sqrt{2}-5\sqrt{2}\\ =-10\sqrt{2}\)
\(8,2\sqrt{3}-\sqrt{75}+2\sqrt{12}-\sqrt{147}\\ =2\sqrt{3}-5\sqrt{3}+2.2\sqrt{3}-7\sqrt{3}\\ =2\sqrt{3}-5\sqrt{3}+4\sqrt{3}-7\sqrt{3}\\ =-6\sqrt{3}\)

\(P^2=\left(\dfrac{\sqrt{x}}{\sqrt{x}+2}\right)^2=\dfrac{\sqrt{x^2}}{x+4\sqrt{x}+4}=\dfrac{x}{x+4\sqrt{x}+4}\)
\(P^2< \dfrac{1}{9}\Leftrightarrow\dfrac{x}{x+4\sqrt{x}+4}< \dfrac{1}{9}\\ \Leftrightarrow\dfrac{9x-x-4\sqrt{x}-4}{9\left(x+4\sqrt{x}+4\right)}< 0\\ \Leftrightarrow8x-4\sqrt{x}-4< 0\)
\(\Leftrightarrow4x-4\sqrt{x}+4x-4< 0\\ \Leftrightarrow4\sqrt{x}\left(\sqrt{x}-1\right)+4\left(x-1\right)< 0\)
\(\Leftrightarrow4\sqrt{x}\left(\sqrt{x}-1\right)+4\left(\sqrt{x}-1\right) \left(\sqrt{x}+1\right)< 0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left[4\sqrt{x}+4\left(\sqrt{x}+1\right)\right]< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1< 0\\8\sqrt{x}+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}< 1\\\sqrt{x}< -\dfrac{4}{8}\left(ktm\right)\end{matrix}\right.\)
\(\Leftrightarrow x< 1\)

Ta có thể sử dụng công thức Newton về đa thức để giải bài toán này. Đặt đa thức $P(x) = (x-a)(x-b)(x-c) = x^3 - (a+b+c)x^2 + (ab+bc+ca)x - abc$.
Do $a+b+c=0$, nên $P(x) = x^3 - 3kx - abc$ với $k = \frac{ab+bc+ca}{a+b+c}$.
Ta có thể tính được $a^2+b^2+c^2 = -2(ab+bc+ca)$.
Đặt $S_n = a^n + b^n + c^n$. Ta có thể suy ra các công thức sau:
$S_1 = 0$
$S_2 = a^2 + b^2 + c^2 = -2(ab+bc+ca)$
$S_3 = 3abc$
$S_4 = (a^2+b^2+c^2)^2 - 2(a^2b^2+b^2c^2+c^2a^2) = 2(ab+bc+ca)^2 - 3abc(a+b+c)$
$S_5 = 5(ab+bc+ca)(a^2+b^2+c^2) - 5abc(a+b+c)$
$S_6 = (a^2+b^2+c^2)^3 - 3(a^2+b^2+c^2)(a^2b^2+b^2c^2+c^2a^2) + 2(a^2b^2c^2)$
$S_7 = 7(ab+bc+ca)(a^2+b^2+c^2)^2 - 14abc(a^2+b^2+c^2) + 7a^2b^2c^2$
Từ đó, ta có thể tính được $S_1, S_2, S_3, S_4, S_5, S_6$ dựa trên các giá trị đã biết.
Đặt $T_n = a^n+b^n+c^n - S_n$. Ta có thể suy ra các công thức sau:
$T_1 = 0$
$T_2 = 2S_2$
$T_3 = 3S_3$
$T_4 = 2S_2^2 - 4S_4$
$T_5 = 5S_2S_3 - 5S_5$
$T_6 = 2S_2S_4 + 3S_3^2 - 6S_6$
$T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7$
Do $S_1=S_3=0$, nên $T_1=T_3=0$.
Từ $a+b+c=0$, ta có $a^2+b^2+c^2 = -2(ab+bc+ca)$. Do đó, $S_2 = 2(ab+bc+ca)$ và $S_4 = 2(ab+bc+ca)^2 - 3abc(a+b+c) = 2(ab+bc+ca)^2$.
Từ $a^7+b^7+c^7=0$, ta có $T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7 = 7S_2S_5 - 14S_4S_3 + 7S_7 = 7S_7$.
Từ $T_7 = 7S_7$, ta có $S_7 = \frac{T_7}{7} = 0$.
Do đó, $T_6 = 2S_2S_4 + 3S_3^2 - 6S_6 = 2(2(ab+bc+ca))(2(ab+bc+ca)^2) + 3(abc)^2 - 6S_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$.
Từ $T_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$, ta có $S_6 = \frac{1}{6}(12(ab+bc+ca)^2 + 3(abc
Giải
Vì a + b + c = 0 nên a + b = -c
Ta có:
\(a^7+b^7=\left(a+b\right)\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =-c\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =c\left(-a^6+a^5b-a^4b^2+a^3b^3-a^2b^4+ab^5-b^6\right)\\ =c\left[-\left(a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6\right)+\left(7a^5b+14a^4b^2+21a^3b^3+14a^2b^4+7ab^5\right)\right]\\ =c\left[-\left(a+b\right)^6+7ab\left(a^4+2a^3b+3a^2b^2+2ab^3+b^4\right)\right]\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)^2+2ab\left(a^2+b^2\right)+3a^2b^2-2a^2b^2\right]\right\}\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =c\left\{-c^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =-c^7+7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\\ \Rightarrow a^7+b^7+c^7=7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\Rightarrow7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]=0\)TH1: \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2=0\)
Vì \(a^2,b^2,\left(a+b\right)^2,a^2b^2\ge0\) nên \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\ge0\)
Dấu "=" xảy ra khi và chỉ khi a = b = 0
Mà a + b + c = 0 nên suy ra c = 0
Vậy \(a^{2023}+b^{2023}+c^{2023}=0\)
TH2: abc = 0
Vì abc = 0 nên sẽ có ít nhất một trong ba số a, b, c = 0
Vì a, b, c có vai trò như nhau nên không mất tính tổng quát, giả sử \(c=0\)
Mà a + b + c = 0 nên a + b =0 hay a = -b
\(\Rightarrow a^{2023}+b^{2023}+c^{2023}=0\)
Kết luận: \(a^{2023}+b^{2023}+c^{2023}=0\)

Lời giải:
Hiển nhiên $\sqrt{2011}> \sqrt{2010}$
$\sqrt{2009}>0$
$\Rightarrow \sqrt{2009}+\sqrt{2011}> \sqrt{2010}$

a) Thay \(b=a-1\) vào hệ thức thứ hai thì được \(a-1+c=a+4\) hay \(c=5\). Hơn nữa, ta thấy \(a>b\) nên \(b\) không thể là độ dài của cạnh huyền của tam giác vuông được. Sẽ có 2 trường hợp:
TH1: \(a\) là độ dài cạnh huyền. Khi đó theo định lí Pythagoras thì \(b^2+c^2=a^2\) \(\Rightarrow b^2+25=\left(b+1\right)^2\) \(\Leftrightarrow b^2+25=b^2+2b+1\) \(\Leftrightarrow2b=24\) \(\Leftrightarrow b=12\), suy ra \(a=13\). Vậy \(\left(a,b,c\right)=\left(13,12,5\right)\)
TH2: \(c\) là độ dài cạnh huyền. Khi đó cũng theo định lý Pythagoras thì \(a^2+b^2=c^2\) \(\Leftrightarrow\left(b+1\right)^2+b^2=25\) \(\Leftrightarrow2b^2+2b-24=0\) \(\Leftrightarrow b^2+b-12=0\) \(\Leftrightarrow\left[{}\begin{matrix}b=3\left(nhận\right)\\b=-4\left(loại\right)\end{matrix}\right.\) \(\Rightarrow a=b+1=4\). Vậy \(\left(a,b,c\right)=\left(4,3,5\right)\)
Như vậy, ta tìm được \(\left(a,b,c\right)\in\left\{\left(13,12,5\right);\left(4,3,5\right)\right\}\)
b) Bạn không nói rõ b', c' là gì thì mình không tính được đâu. Mình tính b, c trước nhé.
Do \(b:c=3:4\) nên rõ ràng \(c>b\). Vì vậy \(b\) không thể là độ dài cạnh huyền được. Sẽ có 2TH
TH1: \(c\) là độ dài cạnh huyền. Khi đó theo định lý Pythagoras thì \(a^2+b^2=c^2\). Do \(b:c=3:4\) nên \(b=\dfrac{3}{4}c\). Đồng thời \(a=125\) \(\Rightarrow125^2+\left(\dfrac{3}{4}c\right)^2=c^2\) \(\Rightarrow\dfrac{7}{16}c^2=125^2\) \(\Leftrightarrow c=\dfrac{500}{\sqrt{7}}\) \(\Rightarrow b=\dfrac{375}{\sqrt{7}}\). Vậy \(\left(b,c\right)=\left(\dfrac{375}{\sqrt{7}},\dfrac{500}{\sqrt{7}}\right)\)
TH2: \(a\) là độ dài cạnh huyền. Khi đó cũng theo định lý Pythagoras, ta có \(b^2+c^2=a^2=125^2\). Lại có \(b:c=3:4\Rightarrow\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{b^2+c^2}{25}=\dfrac{125^2}{25}=625\)
\(\Rightarrow b^2=5625\Rightarrow b=75\) \(\Rightarrow c=100\). Vậy \(\left(b,c\right)=\left(75,100\right)\).
Như vậy, ta tìm được \(\left(b,c\right)\in\left\{\left(75,100\right);\left(\dfrac{350}{\sqrt{7}};\dfrac{500}{\sqrt{7}}\right)\right\}\)


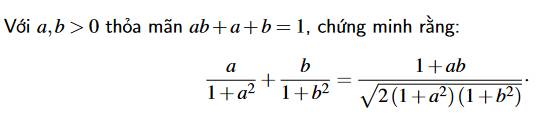


\(\sqrt{x^2+1}-x=3\\ < =>\sqrt{x^2+1}=3+x\\ < =>\left\{{}\begin{matrix}3+x\ge0\\x^2+1=9+6x+x^2\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}x\ge-3\\6x=-8\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}x\ge-3\\x=-\dfrac{4}{3}\left(tm\right)\end{matrix}\right.\\ < =>x=-\dfrac{4}{3}\)
Giải
\(\sqrt{x^2+1}-x=3\\ \Leftrightarrow\sqrt{x^2+1}=3+x\\ \Leftrightarrow\left\{{}\begin{matrix}3+x>0\left(x^2+1\ge0+1=1>0\right)\\x^2+1=\left(3+x\right)^2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>-3\\x^2+1=x^2+6x+9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>-3\\6x=-8\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>-3\\x=-\dfrac{4}{3}\end{matrix}\right.\\ \Leftrightarrow x=-\dfrac{4}{3}\)
Vậy \(S=\left\{-\dfrac{4}{3}\right\}\)