Để giải quyết bài toán này, ta thực hiện các bước sau:

### a) Tính diện tích nền nhà

Nền nhà có dạng hình chữ nhật với chiều dài là 8 mét và chiều rộng bằng một nửa chiều dài.

Chiều rộng của nền nhà:
\[ \text{Chiều rộng} = \frac{1}{2} \times \text{Chiều dài} = \frac{1}{2} \times 8 = 4 \text{ mét} \]

Diện tích của nền nhà được tính bằng công thức diện tích hình chữ nhật:
\[ \text{Diện tích} = \text{Chiều dài} \times \text{Chiều rộng} = 8 \text{ m} \times 4 \text{ m} = 32 \text{ m}^2 \]

### b) Tính số viên gạch cần dùng

Mỗi viên gạch có hình vuông với cạnh là 4 dm (decimet). Ta cần đổi đơn vị của kích thước gạch từ dm sang m để tính diện tích của từng viên gạch.

1 dm = 0,1 m, nên:
\[ \text{Cạnh của viên gạch} = 4 \text{ dm} = 4 \times 0,1 \text{ m} = 0,4 \text{ m} \]

Diện tích của một viên gạch là:
\[ \text{Diện tích của viên gạch} = \text{Cạnh} \times \text{Cạnh} = 0,4 \text{ m} \times 0,4 \text{ m} = 0,16 \text{ m}^2 \]

Số viên gạch cần dùng để lát nền nhà là:
\[ \text{Số viên gạch} = \frac{\text{Diện tích nền nhà}}{\text{Diện tích của một viên gạch}} = \frac{32 \text{ m}^2}{0,16 \text{ m}^2} = 200 \text{ viên} \]

### Kết quả

a) Diện tích nền nhà là \( 32 \text{ m}^2 \).

b) Số viên gạch cần dùng để lát nền nhà là 200 viên.

a) Chiều rộng nền nhà là: 

`8 : 2 = 4 (m)`

Diện tích nền nhà là: 

`8 . 4 = 32 (m^2)`

b) Diện tích 1 viên gạch là: 

`4 . 4 = 16 (dm^2)`

Đổi `16dm^2 = 0,16m^2`

Số viên gạch cần dùng lát nền nhà là: 

`32 : 0,16 = 200` (viên)

Đáp số: ....

\(x^3+ax+b\\ =\left(x^3+4x^2+3x\right)+\left(-4x^2-16x-12\right)+\left(a+13\right)x+\left(b+12\right)\\ =x\left(x^2+4x+3\right)-4\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\\ =\left(x-4\right)\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\)

Để `x^3+ax+b` chia hết cho `x^2+4x+3` thì:

\(\left\{{}\begin{matrix}a+13=0\\b+12=0\end{matrix}\right.=>\left\{{}\begin{matrix}a=-13\\b=-12\end{matrix}\right.\)

Gọi cạnh của hình lập phương đó là `x (cm)`

Điều kiện: `x > 0`

Diện tích toán phần của hình lập phương là: 

`x . x . 6 = 6x^2`

Thể tích hình lập phương là: 

`x . x . x = x^3`

Mà diện tích toàn phần của hình lập phương bằng thể tích của nó

`=> x^3 = 6x^2`

`=> x^3 - 6x^2 = 0`

`=> x^2 (x - 6) = 0`

`=> x = 0` hoặc `x = 6`

Mà `x > 0` nên `x = 6`

Vậy cạnh của hình lập phương là `6cm`

Thể tích hình lập phương là: 

`6^3 = 216 (cm^3)`

Vậy ....

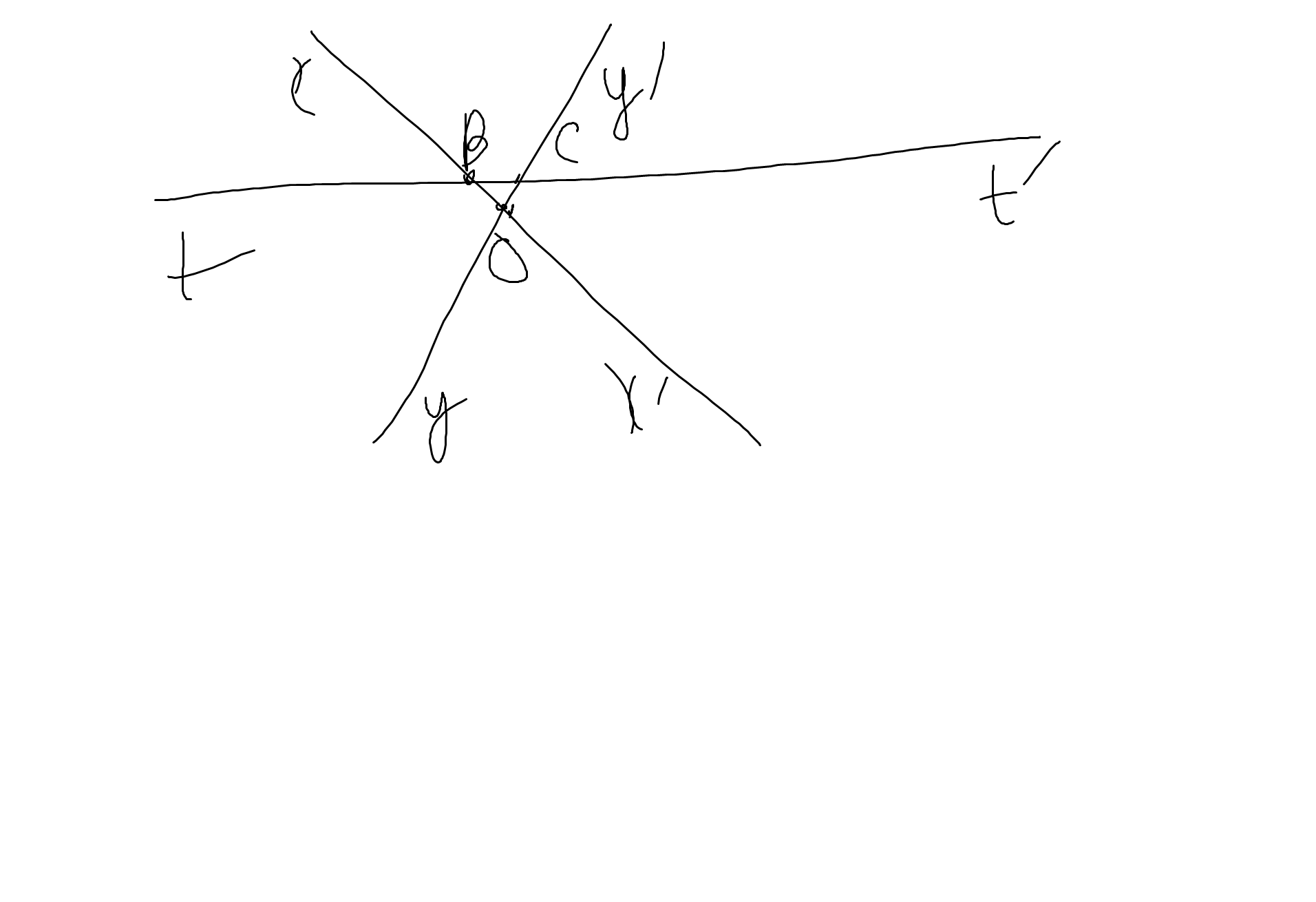
Bài 3: Các cặp góc so le trong là: \(\widehat{tBO};\widehat{BOC}\); \(\widehat{OBC};\widehat{yOB}\); \(\widehat{BCO};\widehat{x'OC}\); \(\widehat{t'CO};\widehat{BOC}\)

Các cặp góc đồng vị là:

\(\widehat{xBt};\widehat{xOy}\); \(\widehat{tBO};\widehat{x'Oy}\); \(\widehat{y'Ct'};\widehat{x'Oy'}\); \(\widehat{t'CO};\widehat{x'Oy}\)

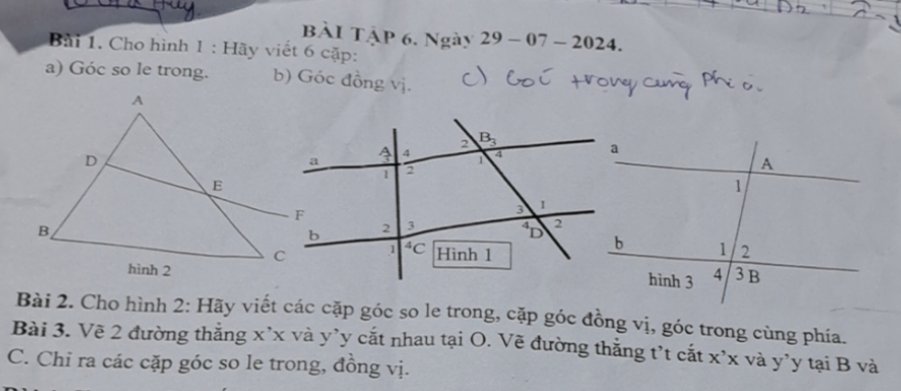
Bài 2: 

Các cặp góc so le trong là \(\widehat{FEC};\widehat{ACB}\)

Các cặp góc đồng vị là \(\widehat{ADE};\widehat{ABC}\); \(\widehat{AED};\widehat{ACB}\)

Các cặp góc trong cùng phía là: \(\widehat{BDE};\widehat{B}\); \(\widehat{DEC};\widehat{ECB}\)

Ta thấy 

b - 1 < b < b + 1

=> b - 1; b; b + 1 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự tăng dần

m < m + 1 < m + 2 

=> m; m + 1; m + 2 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự tăng dần

n + 1 < n + 2 < n + 3

=> n + 1; n + 2; n + 3 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự tăng dần 

c + 1 > c > c - 1 

=> c + 1; c; c - 1 là 3 số tự nhiên liên tiếp sắp xếp theo thứ tự giảm dần 

Chọn phương án số 2 

`-1/3<=x/3<=-1/6`

`=>-2/6<=2x/3<=-1/6`

`=>-2<=2x<=-1`

`=>-2/2<=x<=-1/2`

`=>-1<=x<=-1/2` 

\(\dfrac{-1}{2}< \dfrac{x}{3}< \dfrac{-1}{6}\)

`=>` \(\dfrac{-3}{6}< \dfrac{2x}{6}< \dfrac{-1}{6}\)

`=> -3 < 2x < -1`

Mà `2x` là số nguyên

`=> 2x = -2`

`=> x = -1`

Vậy `x = -1`

`4^3<=2^x<=2^10`

`=>(2^2)^3<=2^x<=2^10`

`=>2^(2*3)<=2^x<=2^10`

`=>2^6<=2^x<=2^10`

`=>6<=x<=10` 

giúp mình với ạ

4,25

vì khoảng cách giữa các số là 0,75

a: Ta có: ΔABC vuông tại A

=>\(BC^2=AB^2+AC^2\)

=>\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)

Xét ΔABC vuông tại A có

\(sinB=\dfrac{AC}{BC}=\dfrac{3}{5};cosB=\dfrac{AB}{BC}=\dfrac{4}{5}\)

b: Xét ΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\BH\cdot BC=BA^2\\CH\cdot CB=CA^2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AH\cdot5=3\cdot4=12\\BH\cdot5=4^2=16\\CH\cdot5=3^2=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2,4\left(cm\right)\\BH=3,2\left(cm\right)\\CH=1,8\left(cm\right)\end{matrix}\right.\)

Xét ΔAHB vuông tại H có HK là đường cao

nên \(AK\cdot AB=AH^2\)

=>\(AK\cdot4=2,4^2\)

=>\(AK=1,44\left(cm\right)\)

Xét ΔAHC vuông tại H có HI là đường cao

nên \(AI\cdot AC=AH^2\)

=>\(AI=\dfrac{2.4^2}{3}=1,92\left(cm\right)\)

c: xét tứ giác AIHK có \(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)

=>AIHK là hình chữ nhật

=>\(S_{AIHK}=AI\cdot AK=1,92\cdot1,44=2,7648\left(cm^2\right)\)