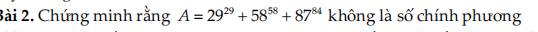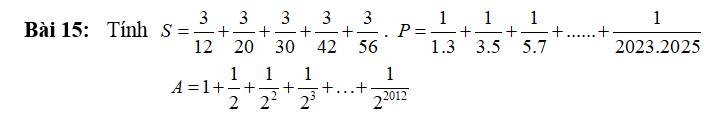a.

Số củ cải là:

\(48\times12,5\%=6\) (củ)

Số cà rốt là:

\(\left(48-6\right)\times\dfrac{3}{7}=18\) (củ)

Số khoai tây là:

\(48-\left(6+18\right)=24\) (củ)

b.

Khoai tây chiếm phần trăm so với tổng số rau củ là:

\(\left(\dfrac{24.100}{48}\right)\%=50\%\)

Quãng đường xe đã đi là:

\(125920,5-125454,7=465,8\left(km\right)\)

Số tiền xăng xe đã tiêu thụ là:

\(\dfrac{465,8}{8,5}\times22700=1243960\) (đồng)

Mỗi người bạn của anh Minh phải trả số tiền là:

\(1243960:4=310990\) (đồng)

Chứng minh dựa trên tính chất: số chính phương chia 4 chỉ có số dư là 0 hoặc 1

Ta có: \(58^{58}=\left(29.2\right)^{58}=29^{58}.2^{58}=4.29^{58}.2^{56}\equiv0\left(mod4\right)\)

\(29\equiv1\left(mod4\right)\Rightarrow29^{29}\equiv1^{29}\left(mod4\right)\Rightarrow29^{29}\equiv1\left(mod4\right)\)

\(87\equiv-1\left(mod4\right)\Rightarrow87^{84}\equiv\left(-1\right)^{84}\left(mod4\right)\Rightarrow87^{84}\equiv1\left(mod4\right)\)

\(\Rightarrow A\equiv1+0+1\left(mod4\right)\Rightarrow A\equiv2\left(mod4\right)\)

\(\Rightarrow A\) chia 4 dư 2 nên A ko là số chính phương

Vận tốc trung bình là:

\(\dfrac{15+10}{2}=12,5\left(\dfrac{km}{h}\right)\)

10/40=1/4=25/100=25%

\(\dfrac{10}{40}\)=\(\dfrac{1}{4}\)=25%

\(S=\dfrac{3}{12}+\dfrac{3}{20}+\dfrac{3}{30}+\dfrac{3}{42}+\dfrac{3}{56}\)

\(=3\left(\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\right)\)

\(=3\left(\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}\right)\)

\(=3\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\right)\)

\(=3\left(\dfrac{1}{3}-\dfrac{1}{8}\right)=1-\dfrac{3}{8}=\dfrac{5}{8}\)

\(P=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{2023\cdot2025}\)

\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2023\cdot2025}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2023}-\dfrac{1}{2025}\right)\)

\(=\dfrac{1}{2}\left(1-\dfrac{1}{2025}\right)=\dfrac{1}{2}\cdot\dfrac{2024}{2025}=\dfrac{1012}{2025}\)

\(A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{2012}}\)

=>\(2A=2+1+...+\dfrac{1}{2^{2011}}\)

=>\(2A-A=2+1+...+\dfrac{1}{2^{2011}}-1-\dfrac{1}{2}-...-\dfrac{1}{2^{2012}}\)

=>\(A=2-\dfrac{1}{2^{2012}}=\dfrac{2^{2013}-1}{2^{2012}}\)

Có 6 set

Cả giải có tất cả 18 set đấu