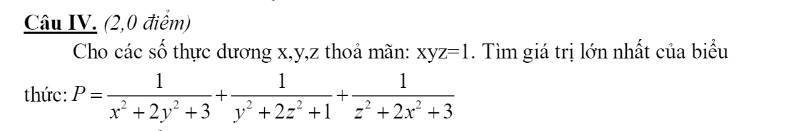\(\left\{{}\begin{matrix}\dfrac{3x}{4}+\dfrac{7y}{3}=41\\\dfrac{5x}{2}-\dfrac{3y}{5}=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+28y=492\\25x-6y=110\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}225x+700y=12300\\225x-54y=990\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}700y+54y=12300-990\\9x+28y=492\end{matrix}\right.\)

\(\)\(\Leftrightarrow\left\{{}\begin{matrix}y=15\\x=8\end{matrix}\right.\)

Vậy (x;y) = (8;15) 

Em đăng đúng môn nhé.

Ta chứng minh \(\left(n,n+1\right)=1\) với mọi số tự nhiên n. Thật vậy, đặt \(\left(n,n+1\right)=d\left(d\inℕ^∗\right)\), khi đó \(\left\{{}\begin{matrix}n⋮d\\n+1⋮d\end{matrix}\right.\) \(\Rightarrow\left(n+1\right)-n⋮d\) \(\Rightarrow1⋮d\Rightarrow d=1\). Vậy \(\left(n,n+1\right)=1\). 

Xét số tự nhiên \(k\) bất kì sao cho \(1\le k\le35\). Theo đề bài kết hợp với \(\left(n,n+1\right)=1\), dễ thấy \(\left(n,n+k\right)\ge k\). Đặt \(\left(n,n+k\right)=d'\left(d'\ge k\right)\), khi đó \(\left\{{}\begin{matrix}n⋮d'\\n+k⋮d'\end{matrix}\right.\Rightarrow\left(n+k\right)-n⋮d'\) \(\Rightarrow k⋮d'\). Nhưng do \(d'\ge k\) nên \(d'=k\). Vì \(n⋮d'\) ,suy ra \(n⋮k\) (đpcm)

b,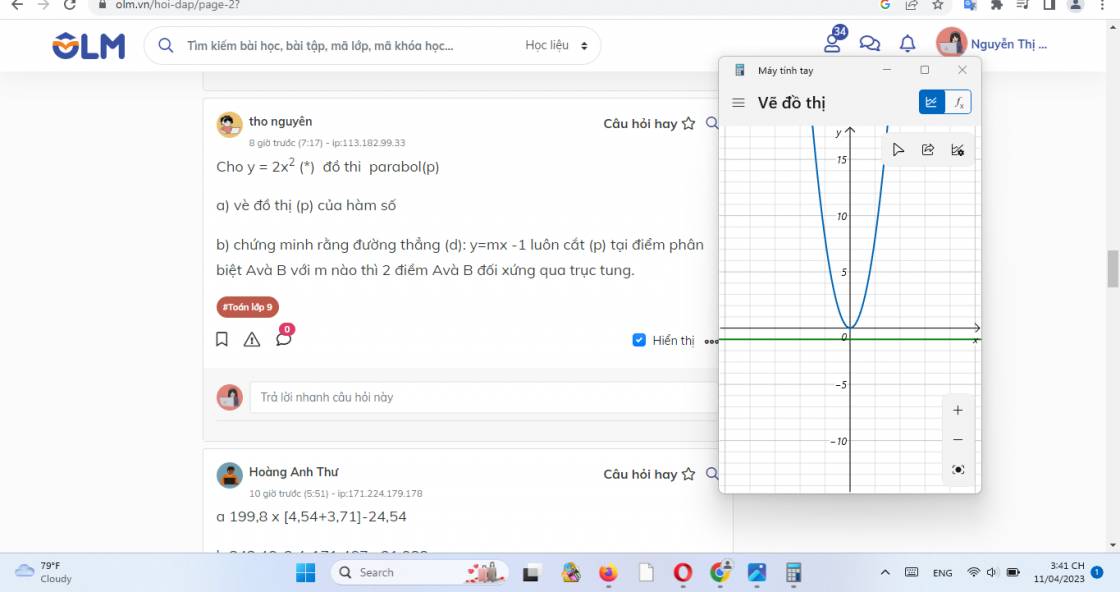 

Giả sử m = 0 thì đt có dạng y = -1

Quan sát hai đồ htij trên hình vẽ em sẽ thấy

parapol (p) và đt d không cắt nhau vậy việc chứng minh (p) và (d) cắt nhau tại hai điểm phân biệt với mọi m là không thể xảy ra 

Lời giải:
Áp dụng BĐT AM-GM ta có:

$P=\sum \frac{1}{(x^2+y^2)+(y^2+1)+2}\leq \sum \frac{1}{2xy+2y+2}$

$=\frac{1}{2}\sum \frac{1}{xy+y+1}$

$=\frac{1}{2}(\frac{1}{xy+y+1}+\frac{1}{yz+z+1}+\frac{1}{xz+x+1})$

$=\frac{1}{2}(\frac{z}{xyz+yz+z}+\frac{1}{yz+z+1}+\frac{yz}{xzyz+xyz+yz})$

$=\frac{1}{2}(\frac{z}{1+yz+z}+\frac{1}{yz+z+1}+\frac{yz}{z+1+yz})$

$=\frac{1}{2}.\frac{1+yz+z}{1+yz+z}=\frac{1}{2}$

Ta có tứ giác AMBC nội tiếp ( O ) nên $\widehat{KMB}=\widehat{ACB}$

Mặt khác $\widehat{BFC}=\widehat{BEC}={90}^0$ nên tứ giác BFEC nội tiếp suy ra $\widehat{KFB}=\widehat{BCE}$

Khi đó $\widehat{KMB}=\widehat{KFB}$ nên tứ giác KMFB nội tiếp

Dễ thấy BFEC là tứ giác nội tiếp nên $\widehat{FBC}=\widehat{FEA}\Rightarrow$ tứ giác EFCB nội tiếp

=> $\widehat{HMA}={90}^0\Rightarrow MH\perp AK$