Rút gọn phân thức Q= 1+x^4+x^8+...+x^2020/1+x^2+x^4+...+x^2022
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(16\cdot\left(2x+3\right)^2-9\cdot\left(5x-2\right)^2\\ =\left(8x+12\right)^2-\left(15x-6\right)^2\\ =\left(8x+12-15x+6\right)\left(8x+12+15x-6\right)\\ =\left(-7x+18\right)\left(23x+6\right)\)


Gọi T là giao điểm của DE và AB. Qua F kẻ đường thẳng song song với BC cắt DA, DT lần lượt tại U, V.
Áp dụng định lý Menelaus cho tam giác ABC, cát tuyến TED, ta có:
\(\dfrac{TA}{TB}.\dfrac{DB}{DC}.\dfrac{EC}{EA}=1\)
Áp dụng định lý Ceva cho tam giác ABC với AD, BE, CF đồng quy tại O, ta có:
\(\dfrac{FA}{FB}.\dfrac{DB}{DC}.\dfrac{EC}{EA}=1\)
Từ đó suy ra \(\dfrac{TA}{TB}=\dfrac{FA}{FB}\Leftrightarrow\dfrac{TA+FA}{TB}=\dfrac{2FA}{TB}\) \(\Leftrightarrow\dfrac{TF}{TB}=\dfrac{2AF}{AB}\)
Mà theo định lý Thales:
\(\dfrac{TF}{TB}=\dfrac{FV}{BD}\) và \(\dfrac{AF}{AB}=\dfrac{FU}{BD}\)
Từ đó suy ra \(\dfrac{FV}{BD}=\dfrac{2FU}{BD}\) \(\Rightarrow FV=2FU\) hay U là trung điểm FV.
Áp dụng bổ đề hình thang, ta dễ dàng suy ra O là trung điểm MN hay \(OM=ON\) (đpcm).
(Bổ đề hình thang phát biểu như sau: Trung điểm của 2 cạnh đáy, giao điểm của 2 đường chéo và giao điểm của 2 đường thẳng chứa 2 cạnh bên của một hình thang thì thẳng hàng. Chứng minh khá dễ, mình nhường lại cho bạn tự tìm hiểu nhé.)

Chỗ biến đổi này mình làm lại nhé:
Cần chứng minh: \(\dfrac{TF}{TB}=\dfrac{2AF}{AB}\)
\(\Leftrightarrow TF.AB=2AF.TB\)
\(\Leftrightarrow\left(TA+AF\right)\left(AF+BF\right)=2AF\left(TA+AF+BF\right)\)
\(\Leftrightarrow TA.AF+TA.BF+AF^2+AF.BF=2TA.AF+2AF^2+2AF.BF\)
\(\Leftrightarrow TA.AF+AF^2+AF.FB=TA.BF\)
\(\Leftrightarrow AF\left(TA+AF+FB\right)=TA.BF\)
\(\Leftrightarrow AF.TB=TA.BF\)
\(\Leftrightarrow\dfrac{TA}{TB}=\dfrac{FA}{FB}\) (luôn đúng)
Vậy \(\dfrac{TF}{TB}=\dfrac{2AF}{AB}\)

a, \(\dfrac{2^3-x^3}{x\left(x^2+2x+4\right)}\) = \(\dfrac{\left(2-x\right)\left(x^2+2x+4\right)}{x\left(x^2+2x+4\right)}\) = \(\dfrac{2-x}{x}\)=\(\dfrac{x-2}{-x}\)(đpcm)
b, \(\dfrac{-3x\left(x-y\right)}{y^2-x^2}\) (\(x\) \(\ne\) \(\pm\) y)
= \(\dfrac{-3x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x\left(y-x\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x}{x+y}\) (đpcm)

a/
Ta có
BC//AD (cạnh đối hình bình hành) => BM//AD
\(\Rightarrow\dfrac{BM}{AD}=\dfrac{MN}{AN}\) (Hệ quả định lý Talet) (1)
BC//AD => CM//AP
\(\Rightarrow\dfrac{CM}{AP}=\dfrac{MN}{AN}\) (Hệ quả định lý Talet) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{BM}{AD}=\dfrac{CM}{AP}\) Mà BM=CM (gt)
=> AP=AD (đpcm)
b/
Ta có
BC//AD => BC//DP \(\Rightarrow\dfrac{BN}{DN}=\dfrac{CN}{PN}\) (Hệ quả định lý Talet)
\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DN}{PN}=\dfrac{BN+DN}{CN+PN}=\dfrac{BD}{CP}=1\)
\(\Rightarrow DN=PN\) => tg DPN cân tại N \(\Rightarrow\widehat{CPD}=\widehat{BDP}\) (góc ở đáy tg cân)
Xét tg BDP và tg CDP có
\(\widehat{CPD}=\widehat{BDP}\) (cmt)
CP=BD (gt)
DP chung
=> tg BDP = tg CDP (c.g.c) => BP=CD
Xét tứ giác BCDP có
BC//DP
BP=CD
=> tứ giác BCDP là hình thang cân \(\Rightarrow\widehat{BPD}=\widehat{CDP}\) (góc ở đáy hình thang cân)
Xét tg ABP và tg ACD có
BP=CD (cmt)
\(\widehat{BPD}=\widehat{CDP}\) (cmt)
AP=AD (cmt)
=> tg ABP = tg ACD (c.g.c) => AB=AC (đpcm)

Nếu bạn không có đáp án cho CH hoặc là không biết cách giải thì ĐỪNG bình luận những câu vô nghĩa vào CH.
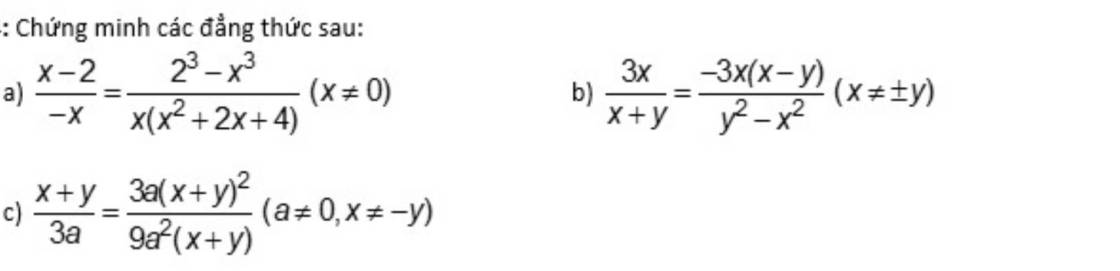
Q = \(\dfrac{1+x^4+x^8+...+x^{2020}}{1+x^2+...+x^{2022}}\)
Đặt A = 1 + \(x^4\) + \(x^8\) +...+ \(x^{2020}\)
Đặt B = 1 + \(x^2\) + ...+ \(x^{2022}\)
Thì Q = \(\dfrac{A}{B}\)
A = 1 + \(x^4\) + \(x^8\) + ...+ \(x^{2020}\)
A.\(x^4\) = \(x^4\) + \(x^8\) +....+ \(x^{2020}\) + \(x^{2024}\)
A.\(x^4\) - A = \(x^{2024}\) - 1
A = \(\dfrac{x^{2024}-1}{x^4-1}\)
B = 1 + \(x^2\) + \(x^4\) +...+ \(x^{2020}\) + \(x^{2022}\)
B.\(x^2\) = \(x^2\) + \(x^4\) +...+ \(x^{2020}\) + \(x^{2022}\) + \(x^{2024}\)
B\(x^2\) - B = \(x^{2024}\) - 1
B = \(\dfrac{x^{2024}-1}{x^2-1}\)
Q = \(\dfrac{\dfrac{x^{2024}-1}{x^4-1}}{\dfrac{x^{2024}-1}{x^2-1}}\)
Q = \(\dfrac{x^{2024}-1}{x^4-1}\) \(\times\)\(\dfrac{x^2-1}{x^{2024}-1}\)
Q = \(\dfrac{1}{x^2+1}\)