khảo sát sự biến thiên và đồ thị của hàm số y=x3+3x+1
giúp nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

hàm số đã cho xác định và liên tục trên đoạn \(\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]\)
f'(x) = 2 - 2sin(2x) = 0 => sin(2x) = 1 => \(x=\dfrac{\pi}{4}\in\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]\text{}\)
ta có: \(f\left(\dfrac{\pi}{12}\right)=\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{2}< f\left(\dfrac{\pi}{4}\right)=\dfrac{\pi}{2}\)
vậy \(\max\limits_{x\in\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]}y=f\left(\dfrac{\pi}{4}\right)=\dfrac{\pi}{2}\)
=> C

\(y'=x^2+2mx+2m-1\)
Hàm có cực trị khi \(\Delta'>0\)
\(\Rightarrow m^2-2m+1>0\)
\(\Rightarrow m\ne1\)

\(y=\dfrac{-x^2+mx-2}{x+1}\)
\(y'=\dfrac{\left(-2x+m\right)\left(x+1\right)-\left(-x^2+mx-2\right)}{\left(x+1\right)^2}=\dfrac{-x^2-2x+m+2}{\left(x+1\right)^2}\)
Hàm nghịch biến trên các khoảng xác định khi:
\(-x^2-2x+m+2\le0;\forall m\)
\(\Leftrightarrow\Delta'=1+\left(m+2\right)\le0\)
\(\Rightarrow m\le-3\)

\(y=\dfrac{2x+1}{x+3}\Rightarrow y'=\dfrac{5}{\left(x+3\right)^2}>0;\forall x\in TXĐ\)
\(y=-x^4+2x^2+1\Rightarrow y'=-4x^3+4x=0\Rightarrow x=\left\{-1;0;1\right\}\) có cực trị nên có các khoảng ĐB, NB (có thể nhớ nhanh là hàm bậc 4 ko bao giờ ĐB hoặc nghịch biến trên R)
\(y=3x^3+x-3\Rightarrow y'=9x^2+1>0;\forall x\)
Vậy (I) và (III) đồng biến trên các khoảng xác định
A đúng

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow\widehat{DSA}\) là góc giữa SD và (SAB)
\(\Rightarrow\widehat{DSA}=60^0\)
\(\Rightarrow SA=\dfrac{AD}{tan60^0}=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{S.ABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{18}\)

Bán kính hình tròn B gấp 3 lần bán kính hình tròn A nên chu vi hình tròn B gấp 3 lần chu vi hình tròn A. Do đó hình tròn A lăn xung quanh hình tròn B 3 vòng thì trở lại điểm xuất phát
Vì bán kính hình tròn B gấp 3 lần bán kính hình tròn B nên ta có đường kính hình tròn B gấp 3 lần đường kính hình tròn A
Hay ta có chu vi hình tròn B gấp 3 lần chu vi hình tròn A
Từ đó ta suy ra được hình tròn A cần xoay quanh hình tròn B 3 lần thì sẽ quay về điểm xuất phát
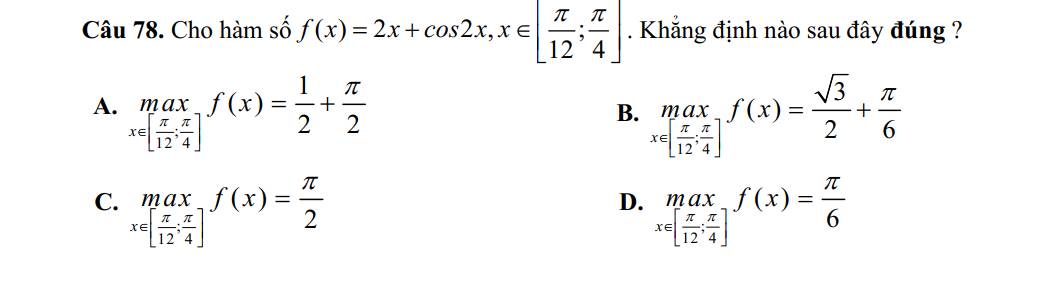

bạn xem lại sách nhé. tính f', tìm nghiệm f'=0, xét dấu f', xác định tính đơn điệu của hàm số, tìm các điểm cực trị. Vẽ đồ thị hàm số
éo biết