Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(F\left(x\right)=7x^2\left(x^2-5x+2\right)-5x\left(x^3-7x^2+3x\right)\)
\(=7x^4-35x^3+14x^2-5x^4+35x^3-15x^2\)
\(=2x^4-x^2\)

\(C=\dfrac{1}{3}-\dfrac{2}{3^2}+\dfrac{3}{3^3}-\dfrac{4}{3^4}+...+\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}\)
\(3C=1-\dfrac{2}{3}+\dfrac{3}{3^2}-\dfrac{4}{3^3}+...+\dfrac{99}{3^{98}}-\dfrac{100}{3^{99}}\)
\(C+3C=1-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{98}}-\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
\(4C=1-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{98}}-\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
\(12C=3-1+\dfrac{1}{3}-\dfrac{1}{3^2}+...+\dfrac{1}{3^{97}}-\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\)
\(4C+12C=3-\dfrac{101}{3^{99}}-\dfrac{100}{3^{100}}\)
\(16C=3-\dfrac{101}{3^{99}}-\dfrac{100}{3^{100}}< 3\)
\(\Rightarrow C< \dfrac{3}{16}\)

Ta có \(x^2,y^2\) khi chia cho 4 thì chỉ có thể có các số dư là 0 hoặc 1.
\(\Rightarrow x^2+y^2\) chia 4 chỉ có thể dư 0, 1, hoặc 2.
Nhưng 2019 chia 4 dư 3. Ta thấy có vô lí.
Vậy không có bộ số \(\left(x,y,z\right)\) nguyên nào thỏa mãn đk đã cho.
(Đề bài này khá lạ khi yêu cầu tìm \(x,y,z\) nhưng trong đk thì lại không có ẩn \(z\).)

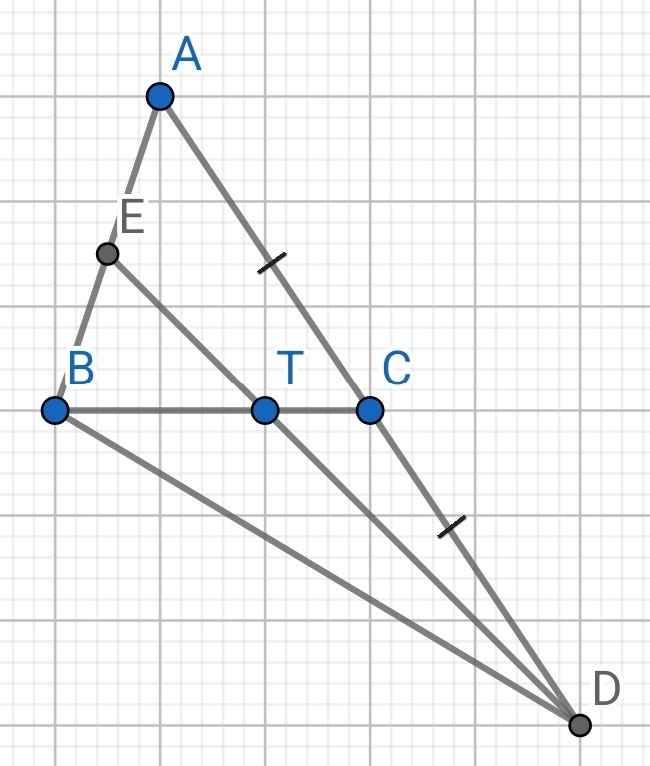
a) Do CA = CD (gt)
⇒ C là trung điểm của AD
⇒ BD là đường trung tuyến của ∆ABD
Mà BT = 2TC (gt)
⇒ T là trọng tâm của ∆ABD
b) Do T là trọng tâm của ∆ABD (cmt)
⇒ T là giao điểm của ba đường trung tuyến của ∆ABD
⇒ DT là đường trung tuyến của ∆ABD
Mà E là giao điểm của DT và AB (gt)
⇒ E là trung điểm của AB

Sửa đề: ΔABC vuông tại A
a: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
Do đó: ΔBAH=ΔBDH
b: Ta có: ΔBAH=ΔBDH
=>\(\widehat{ABH}=\widehat{DBH}\)
Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: Ta có: EA=ED
mà EA<EM(ΔEAM vuông tại A)
nên ED<EM

Sửa đề: ΔABC vuông tại A
a: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
Do đó: ΔBAH=ΔBDH
b: Ta có: ΔBAH=ΔBDH
=>\(\widehat{ABH}=\widehat{DBH}\)
Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: Ta có: EA=ED
mà EA<EM(ΔEAM vuông tại A)
nên ED<EM

Đặt \(\dfrac{x}{-4}=\dfrac{y}{-7}=\dfrac{z}{3}=k\)
=>\(x=-4k;y=-7k;z=3k\)
\(A=\dfrac{-2x+y+3z}{2x-3y-6z}\)
\(=\dfrac{-2\cdot\left(-4k\right)+\left(-7k\right)+3\cdot3k}{2\cdot\left(-4k\right)-3\cdot\left(-7k\right)-6\cdot3k}\)
\(=\dfrac{8k-7k+9k}{-8k+21k-18k}\)
\(=\dfrac{10}{-26+21}=-2\)

a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=30^0\)
b: Sửa đề: ΔBAD=ΔBED
Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
c:
Ta có: AM=AB
mà A nằm giữa M và B
nên A là trung điểm của MB
Xét ΔDBM có
DA là đường trung tuyến
DA là đường cao
Do đó: ΔDBM cân tại D
=>DB=DM
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
ΔDBM cân tại D
=>\(\widehat{DBM}=\widehat{DMB}\)
=>\(\widehat{DMB}=30^0\)