\(\dfrac{a+13}{a+11}=\dfrac{a+11+2}{a+11}=1+\dfrac{2}{a+11}\)

\(\dfrac{a+2023}{a+2021}=\dfrac{a+2021+2}{a+2021}=1+\dfrac{2}{a+2021}\)

Vì: \(\dfrac{2}{a+11}>\dfrac{2}{a+2021}\) nên \(\dfrac{a+13}{a+11}>\dfrac{a+2023}{a+2021}\)

giúp mình với mấy bạn mình cảm ơn

            Giải:

A = 1,27 + 2,77 + 4,27 + 5,77 + ... + 14,77

Dãy số trên là dãy số cách đều với khoảng cách là:

    2,77  - 1,27 = 1,5

Số số hạng của dãy số trên là:

   (14,77 - 1,27) : 1.5   + 1 =  10

Tổng của dãy số trên là:

   A = (14,77 + 1,27) x 10 : 2 = 80,2 

Vậy A = 80,2 

1:

6,52:2

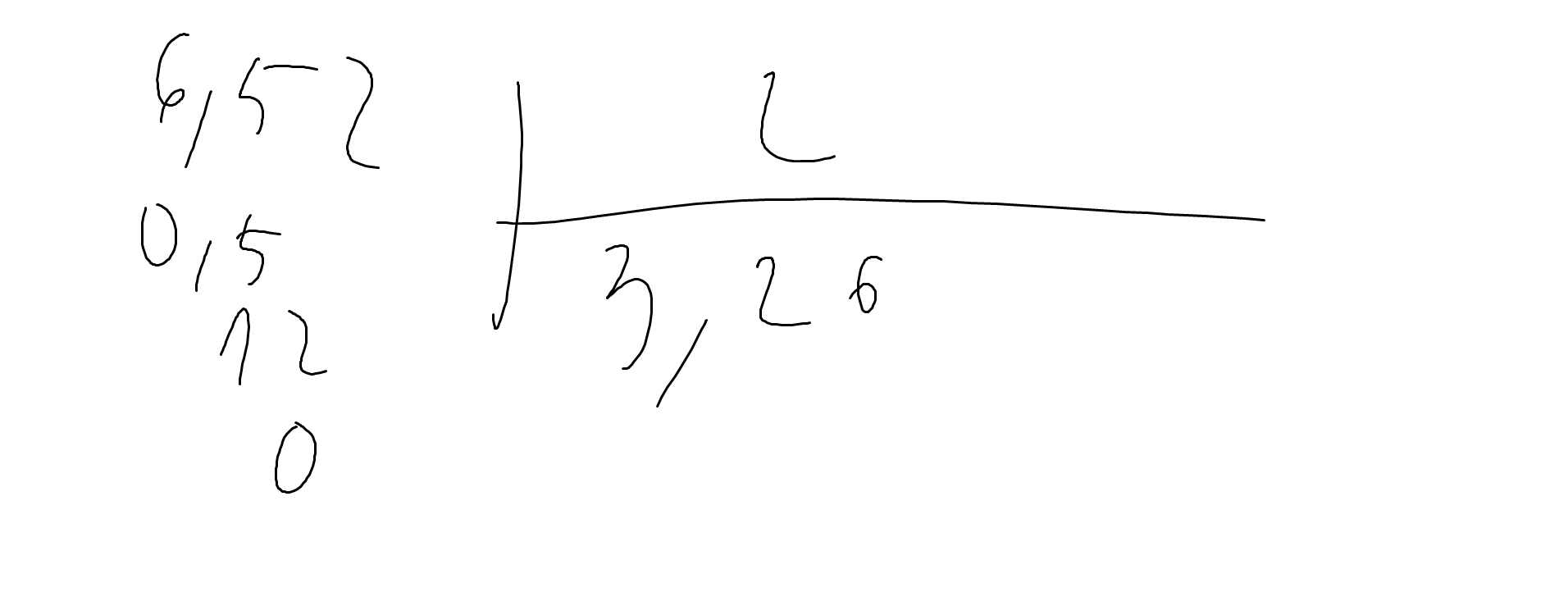
72:15

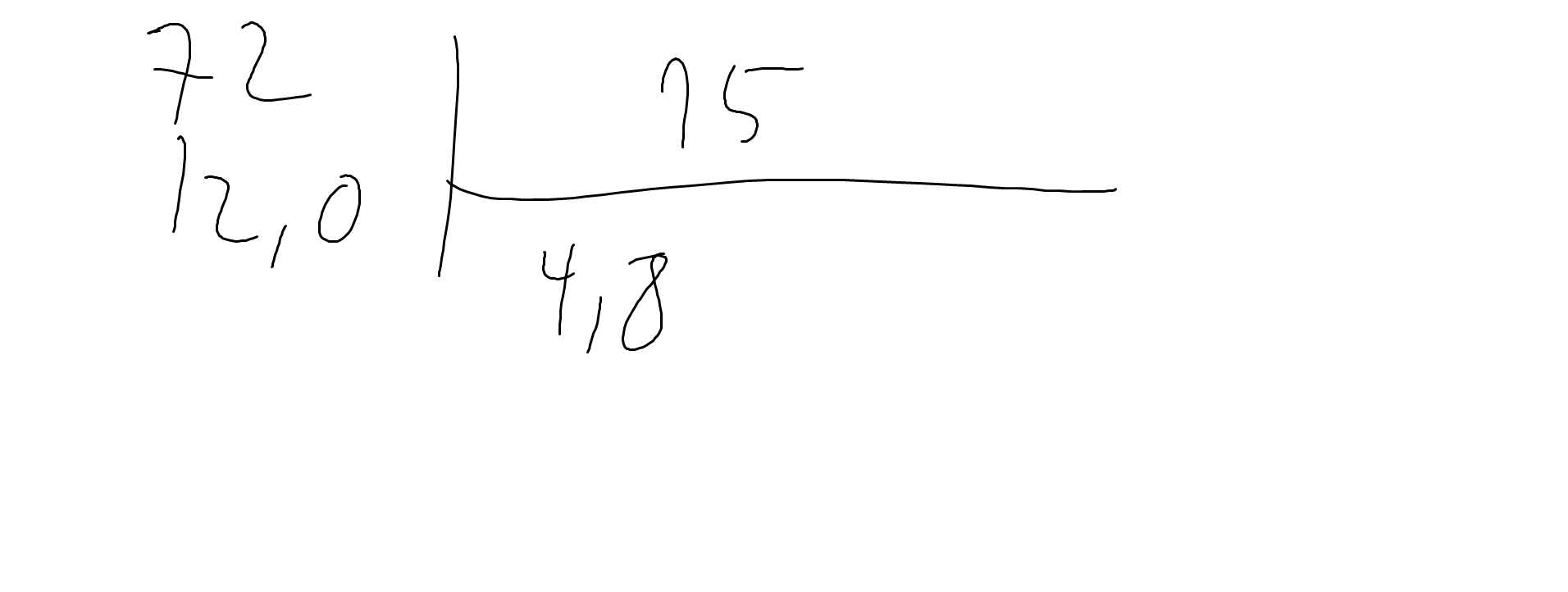
2,52:2,1=25,2:21

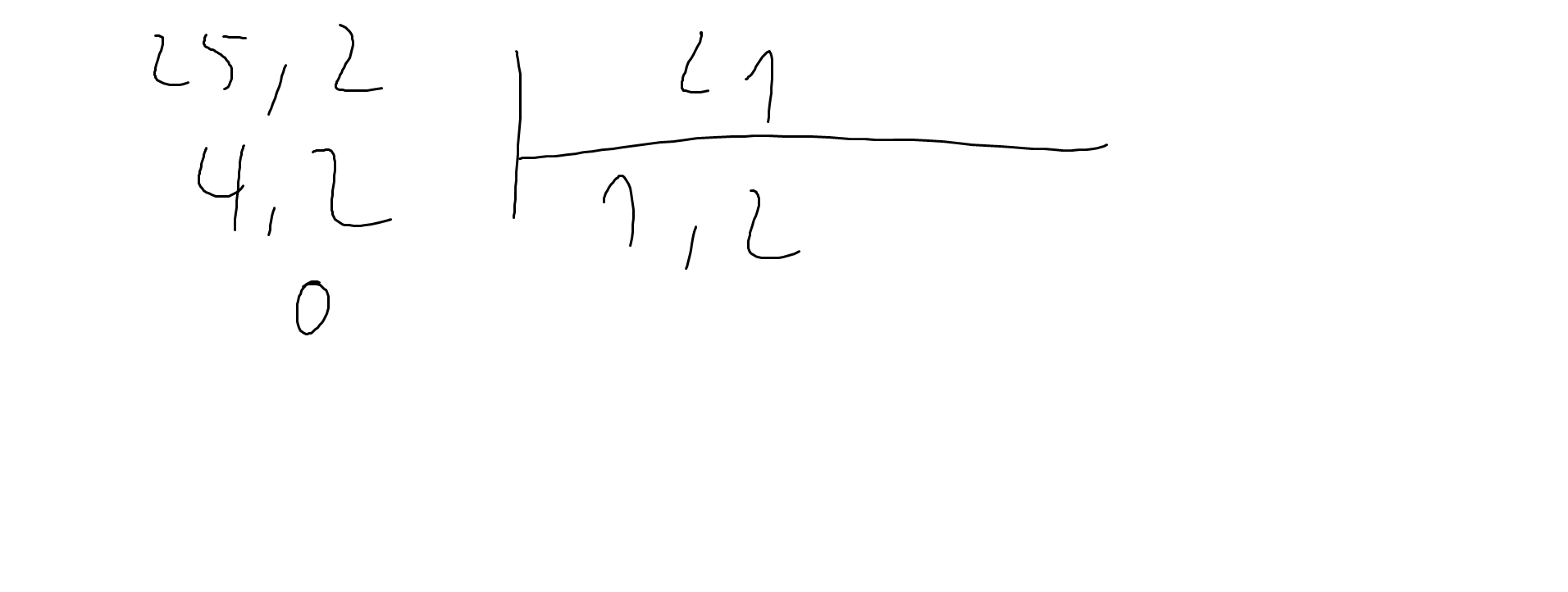
42:1,4=420:14

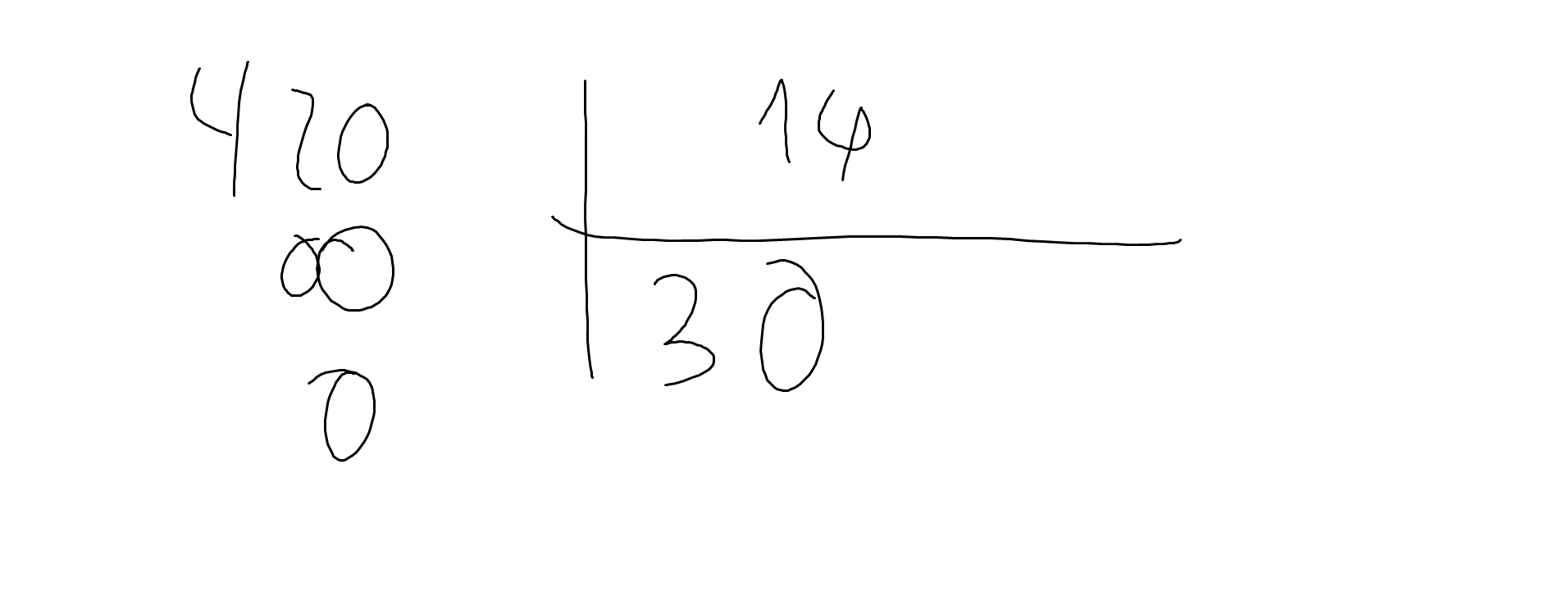
2:

396:8,8=3960:88

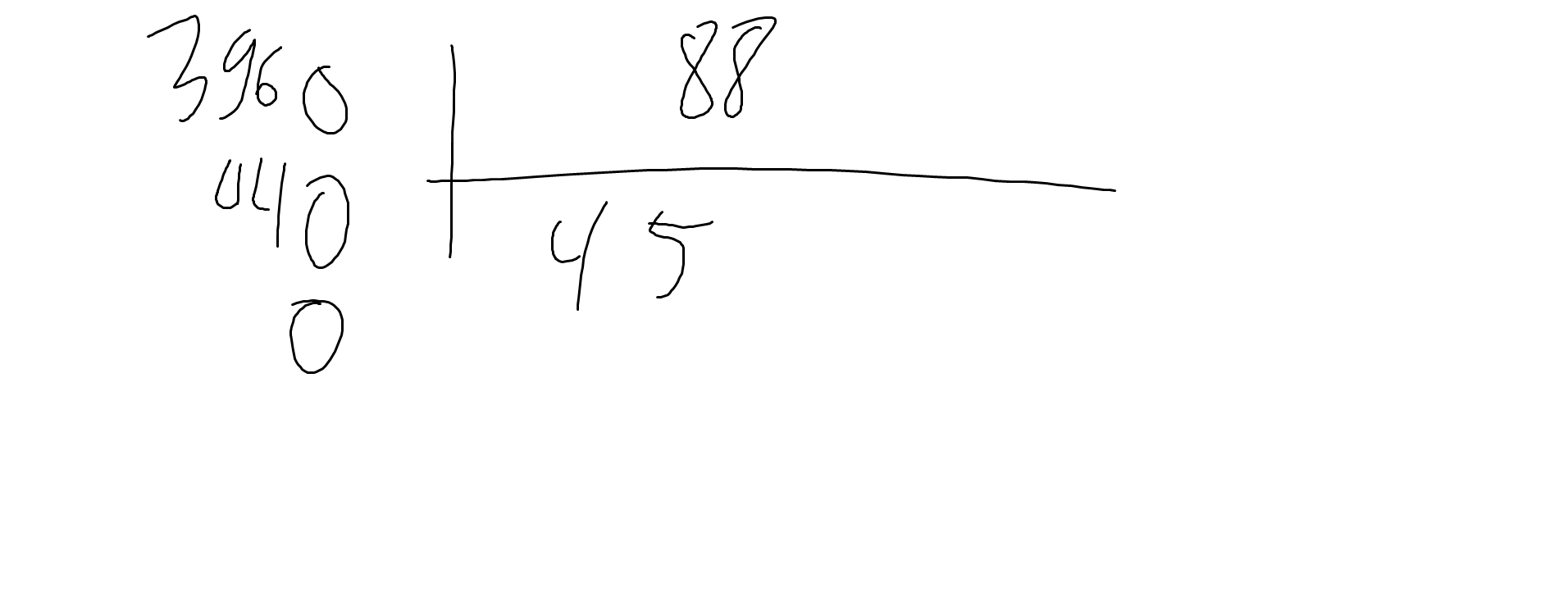
42:2,4=420:24

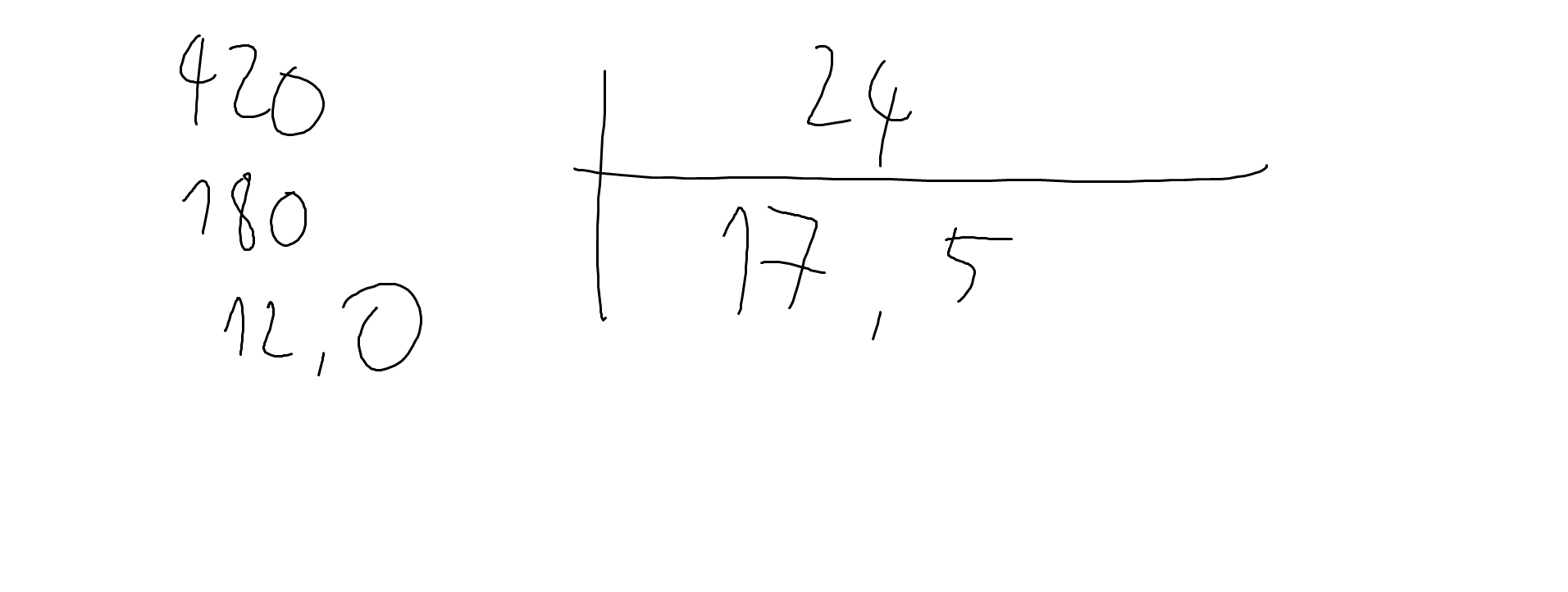
9:0.16=900:16

`2014 mm = 2014/1000 m = 2,014m`

\(\dfrac{28}{36}=\dfrac{28\div4}{36\div4}=\dfrac{7}{9}\)

\(\dfrac{21}{81}=\dfrac{21\div3}{81\div3}=\dfrac{7}{27}\)

\(\dfrac{150}{100}=\dfrac{150\div50}{100\div50}=\dfrac{3}{2}\)

\(\dfrac{70}{80}=\dfrac{70\div10}{80\div10}=\dfrac{7}{8}\)

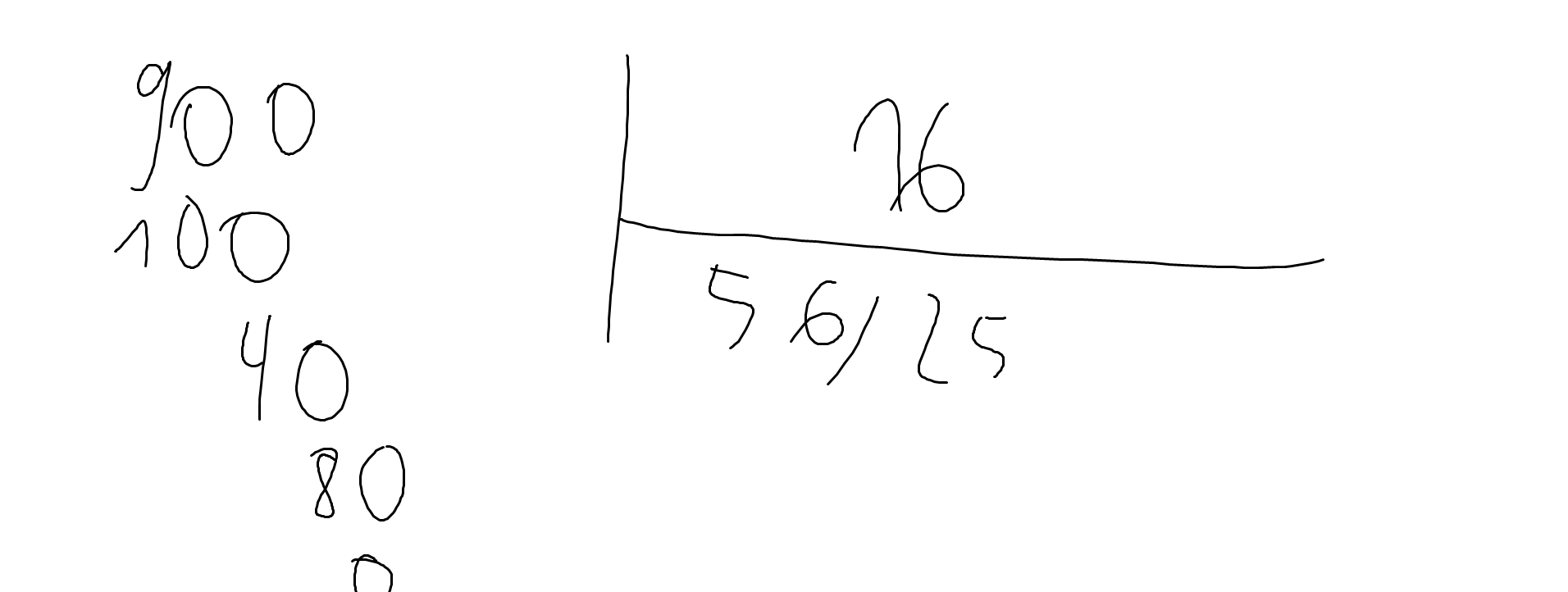
Để tính diện tích của hình thang BCED, chúng ta cần tìm chiều dài đáy lớn và chiều cao của hình thang.

Vì tứ giác BCED là hình thang, ta biết rằng đáy nhỏ BC và đáy lớn ED có độ dài bằng nhau. Gọi độ dài đáy lớn là x.

Theo định lý Pythagoras trong tam giác vuông ABC, ta tính được độ dài cạnh còn lại BC:

BC² = AB² + AC²

BC² = 60² + 80²

BC² = 3600 + 6400

BC = √10000

BC = 100 cm

Vì BC và ED là hai đường chéo của hình thang, nên chúng bằng nhau. Vậy x = 100 cm.

Để tính diện tích hình thang BCED, ta sử dụng công thức:

Diện tích = 0.5 * (đáy nhỏ + đáy lớn) * chiều cao

Diện tích = 0.5 * (BC + ED) * chiều cao

Diện tích = 0.5 * (100 + 100) * 30

Diện tích = 0.5 * 200 * 30

Diện tích = 3000 cm²

Vậy diện tích của hình thang BCED là 3000 cm².

\(\dfrac{1}{2}\times\dfrac{3}{4}+\dfrac{1}{2}\times\dfrac{5}{4}+23\)

\(=\dfrac{1}{2}\times\left(\dfrac{3}{4}+\dfrac{5}{4}\right)+23\)

\(=\dfrac{1}{2}\times2+23\)

\(=1+23\)

\(=24\)

Bạn kiểm tra lại dữ kiện đề nhé, mình tính ra thì số học sinh lại là số thập phân.

          Đây là toán nâng cao chuyên đề hai tỉ số trong đó có một đại lượng không đổi, cấu trúc thi chuyên, thi học sinh giỏi các cấp.Hôm nay. Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau: 

                                           Giải:

   + Vì không có bạn nào chuyển đến hoặc chuyển đi nên số học sinh của cả lớp luôn không đổi.

+ Số học sinh giỏi kí 2 là: 1 : (1 + 5) = \(\dfrac{1}{6}\) (số học sinh cả lớp)

 2 học sinh ứng với:

       \(\dfrac{1}{6}\) - \(\dfrac{1}{9}\) = \(\dfrac{1}{18}\) (cả lớp)

Số học sinh cả lớp là:

        2 : \(\dfrac{1}{18}\) = 36 (học sinh)

Đáp số: 36 học sinh. 

\(\dfrac{1}{2}:0,5-\dfrac{1}{4}:0,25+\dfrac{1}{8}:0,125-\dfrac{1}{10}:0,1\)

\(=\dfrac{1}{2}\times2-\dfrac{1}{4}\times4+\dfrac{1}{8}\times8-\dfrac{1}{10}\times10\)

\(=1-1+1-1\)

\(=0\)

mình cảm ơn nhé