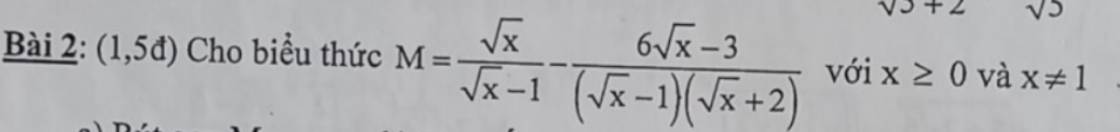\(M=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}-\dfrac{6\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x+2\sqrt{x}-6\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{x-4\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)

đk x >= 0 ; x khác 1 

\(M=\dfrac{x+2\sqrt{x}-6\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)

đk x >= 0 ; x khác 1 

\(B=\dfrac{x-5-2\sqrt{x}-2+4\sqrt{x}+4}{x-1}=\dfrac{x+2\sqrt{x}-3}{x-1}=\dfrac{\sqrt{x}+3}{\sqrt{x}+1}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)

\(x_1^2+2mx_2-x_1-x_2+x_1x_2=6\)

\(\Leftrightarrow x_1\left(x_1+x_2\right)+2mx_2-x_1-x_2=6\)

\(\Leftrightarrow2mx_1+2mx_2-x_1-x_2=6\)

\(\Leftrightarrow2m\left(x_1+x_2\right)-\left(x_1+x_2\right)=6\)

\(\Leftrightarrow\left(2m-1\right)\left(x_1+x_2\right)=6\)

\(\Leftrightarrow2m\left(2m-1\right)=6\)

\(\Leftrightarrow2m^2-m-3=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=\dfrac{3}{2}\end{matrix}\right.\)

j

- Sửa đề: CMR: M,N,P,Q thẳng hàng.

* AM, AN, AP, AQ cắt BC lần lượt tại F,G,H,I.

- \(\Delta AMB\) và \(\Delta FMB\) có: \(\widehat{AMB}=\widehat{FMB}=90^0;\widehat{ABM}=\widehat{FBM};BM\) là cạnh chung.

\(\Rightarrow\Delta AMB=\Delta FMB\left(g-c-g\right)\)

\(\Rightarrow MA=MF\) nên \(M\) là trung điêm AF.

- Tương tự: N là trung điểm AG, P là trung điểm AH, Q là trung điểm AI.

\(\Rightarrow MN,NP,PQ\) lần lượt là đường trung bình của \(\Delta AFG,\Delta AGH,\Delta AHI\)

\(\Rightarrow MN\)//NP//PQ//BC.

\(\Rightarrow\)M,N,P,Q thẳng hàng.

\(=\dfrac{\sqrt{a}\left(\sqrt{ab}+1\right)-\sqrt{b}\left(\sqrt{ab}+1\right)}{\left(\sqrt{ab}-1\right)\left(\sqrt{ab}+1\right)}\)

\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{ab}+1\right)}{\left(\sqrt{ab}-1\right)\left(\sqrt{ab}+1\right)}\)

\(=\dfrac{\sqrt{a}-\sqrt{b}}{\sqrt{ab}-1}\)

Lời giải:
a. Áp dụng định lý về hệ thức lượng trong tam giác vuông cho tam giác $ABH$ có:

$AD.AB=AH^2(1)$
Tương tự với tam giác $AHC$: $AE.AC=AH^2(2)$

Từ $(1); (2)\Rightarrow AD.AB=AE.AC$

$\Rightarrow \frac{AD}{AE}=\frac{AC}{AB}$

-------------------

ĐPCM $\Leftrightarrow \frac{BD^2}{BC^2}=\frac{BH^3}{BC^3}$

$\Leftrightarrow BD^2.BC=BH^3(*)$
Thật vậy:

Do $DH\parallel AC$ nên $\frac{BD}{BA}=\frac{BH}{BC}$

$\Rightarrow BD.BC=BH.BA$

$\Rightarrow BD^2.BC=\frac{BH^2.BA^2}{BC}=\frac{BH^2.BH.BC}{BC}$ (theo hệ thức lượng trong tgv) 

$=BH^3$ 

$(*)$ được chứng minh

Áp dụng hệ thức lượng trong tam giác vuông BDH với đường cao HD:

\(BH^2=BD.AB\)

Xét hai tam giác vuông BDH và BAC có \(\widehat{B}\) chung

\(\Rightarrow\Delta_VBDH\sim\Delta_VBAC\left(g.g\right)\)

\(\Rightarrow\dfrac{BD}{AB}=\dfrac{BH}{BC}\Rightarrow BD=\dfrac{BH.AB}{BC}\)

\(\Rightarrow BD^2=\dfrac{BH.BD.AB}{BC}=\dfrac{BH^3}{BC}\)

\(\Rightarrow\dfrac{BD^2}{BC^2}=\dfrac{BH^3}{BC^3}\)

\(\Rightarrow\sqrt[3]{\dfrac{BD^2}{BC^2}}=\dfrac{BH}{BC}\) (đpcm)