2.5 = 10 = 3.\(x\) ⇒ \(x\) =  \(\dfrac{10}{3}\) ; 2 < \(\dfrac{10}{3}\) < 5 (thỏa mã)

2.3 = 5.\(x\) ⇒ \(x\) = \(\dfrac{6}{5}\);           \(\dfrac{6}{5}\) < 2 loại

3.5  = 2.\(x\) ⇒ \(x\) = \(\dfrac{15}{2}\) > 5 (loại)

Vậy \(x\) = \(\dfrac{10}{3}\)

Ta có tam giác ABC và tia phân giác AD cắt BC tại D, BD=2DC. Kẻ DE vuông góc AB và DF vuông góc AC.

Gọi E là hình chiếu vuông góc của D lên AB, F là hình chiếu vuông góc của D lên AC.

Ta có:

• Tam giác ADE và tam giác ABC đồng dạng (theo góc vuông và góc A), nên AE/AB = DE/DC = AD/AC.
• Tam giác ADF và tam giác ABC đồng dạng (theo góc vuông và góc A), nên AF/AC = DF/DB = AD/AB.

Từ BD=2DC, ta có DC=1/3BC và BD=2/3BC.

Gọi x là độ dài BC, ta có DC=1/3x và BD=2/3x.

Áp dụng vào AE/AB = DE/DC = AD/AC, ta có AE/AB = DE/(1/3x) = AD/AC. Tương tự, áp dụng vào AF/AC = DF/DB = AD/AB, ta có AF/AC = DF/(2/3x) = AD/AB.

Từ hai phương trình trên, ta có hệ phương trình: AE/AB = DE/(1/3x) = AD/AC AF/AC = DF/(2/3x) = AD/AB

Giải hệ phương trình trên ta sẽ tìm được các độ dài của các đoạn thẳng AE, DE, AF, DF.

a/

Xét tg vuông PQI và tg vuông HQI có

QI chung

\(\widehat{PQI}=\widehat{HQI}\left(gt\right)\)

=> tg PQI = tg HQI (hai tg vuông có cạnh huyền và 1 góc nhọn bằng nhau)

c/

Xét tg PQH có

tg PQI = tg HQI (cmt) => PQ=HQ => th PQH cân tại Q

\(\widehat{PQI}=\widehat{HQI}\left(gt\right)\)

\(\Rightarrow PH\perp QI\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao)

d/

Xét tg QKR có

PQ=HQ (cmt)

PK=HR (gt)

=> PQ+PK=HQ+HR => QK=QR => tg QKR cân tại Q

\(\widehat{PQI}=\widehat{HQI}\left(gt\right)\)

\(\Rightarrow QI\perp KR\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao)

Ta có

\(RP\perp QK\)

\(\Rightarrow KI\perp QR\) (trong tg 3 đường cao đồng quy)

Mặt khác \(IH\perp QR\left(gt\right)\)

=> H; I; K thẳng hàng (Từ 1 điểm ngoài đường thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho)

nhìn hình ta thấy! tốt ko?

\(\dfrac{x-1}{33}=\dfrac{4}{x}\left(x\ne0\right)\\ =>x\left(x-1\right)=4.33\\ =>x^2-x-132=0\\ =>\left(x^2-12x\right)+\left(11x-132\right)=0\\ =>x\left(x-12\right)+11\left(x-12\right)=0\\ =>\left(x-12\right)\left(x+11\right)=0\\ =>\left[{}\begin{matrix}x-12=0\\x+11=0\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=12\\x=-11\end{matrix}\right.\)

\(\dfrac{x+4}{20}=\dfrac{5}{x+4}\left(x\ne-4\right)\\ =>\left(x+4\right)^2=20.5\\ =>\left(x+4\right)^2=100=\left(\pm10\right)^2\\ =>\left[{}\begin{matrix}x+4=10\\x+4=-10\end{matrix}\right.\\ =>\left[{}\begin{matrix}x=6\\x=-14\end{matrix}\right.\) (TMDK)

a) \(\dfrac{2x+3}{24}=\dfrac{3x-1}{32}\\ =>32\left(2x+3\right)=24\left(3x-1\right)\\ =>64x+96=72x-24\\ =>72x-64x=24+96\\ =>8x=120\\ =>x=120:8\\ =>x=15\)

b) \(\dfrac{13x-2}{2x+5}=\dfrac{76}{17}\\=>76\left(2x+5\right)=17\left(13x-2\right)\\ =>152x+380=221x-34\\ =>221x-152x=34+380\\ =>69x=414\\ =>x=414:69\\ =>x=6\)

a.

\(\dfrac{2x+3}{24}=\dfrac{3x-1}{32}\)

\(\Leftrightarrow\dfrac{4\left(2x+3\right)}{4.24}=\dfrac{3\left(3x-1\right)}{32.3}\)

\(\Leftrightarrow\dfrac{8x+12}{96}=\dfrac{9x-3}{96}\)

\(\Leftrightarrow8x+12=9x-3\)

\(\Leftrightarrow9x-8x=12+3\)

\(\Leftrightarrow x=15\)

b.

ĐKXĐ: \(x\ne-\dfrac{5}{2}\)

\(\dfrac{13x-2}{2x+5}=\dfrac{76}{17}\)

\(\Leftrightarrow\dfrac{17\left(13x-2\right)}{17\left(2x+5\right)}=\dfrac{76\left(2x+5\right)}{17\left(2x+5\right)}\)

\(\Rightarrow17\left(13x-2\right)=76\left(2x+5\right)\)

\(\Leftrightarrow221x-34=152x+380\)

\(\Leftrightarrow69x=414\)

\(\Leftrightarrow x=6\)

Số lượng nhân công cần dùng để hoàn thiện con đường: (45 x 10) x 2 = 900 (nhân công)

Số lượng công nhân cần trong mỗi ngày thuộc 5 ngày cuối: (900 - 450) : 5 = 90 (công nhân)

Số công nhân cần bổ sung trong 5 ngày cuối: 90 - 45 = 45 (công nhân)

Đ.số:....

Một ngày một công nhân làm được là: \(\dfrac{1}{2}\) : 10 : 45 = \(\dfrac{1}{900}\) (công việc)

Để hoàn thành \(\dfrac{1}{2}\) công việc còn lại thì một công nhân làm trong:

          \(\dfrac{1}{2}\) : \(\dfrac{1}{900}\) = 450 (ngày)

Số ngày để hoàn thành công việc còn lại cho đúng kế hoạch là:

              15   - 10 =  5 (ngày)

Đề hoàn thành \(\dfrac{1}{2}\) công việc còn lại trong 5 ngày cần số công nhân là:

           450 : 5  = 90 (công nhân)

Để hoàn thành phần công việc còn lại tronh 5 ngày thì cần bổ sung số công nhân là: 

             90   - 45  = 45 (công nhân)

Kết luận:...

a/

Xét tg vuông ABD và tg vuông EBD có

BD chung; \(\widehat{ABD}=\widehat{CBD}\left(gt\right)\)

=> tg ABD = tg EBD (hai tg vuông có cạnh huyền và 1 góc nhọn bằng nhau) => AB=BE

b/

Xét tg ABE có

AB=BE (cmt) => tg ABE cân tại B

Mà BD là phân giác của \(\widehat{B}\) (gt) => BD là đường cao của tg ABE (Trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao) \(\Rightarrow AE\perp BD\)

c/

Xét tg vuông ABC và tg vuông EBH có

AB=BE (cmt)

\(\widehat{ACB}=\widehat{EHB}\) (cùng phụ với \(\widehat{B}\) )

=> tg ABC = tg EHB (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau) => BH=BC

d/

C/m tương tự câu (b) khi xét tg BCH

\(\Rightarrow HC\perp BD\)

Mà \(AE\perp BD\left(cmt\right)\)

=> AE//HC (cùng vuông góc với BD)

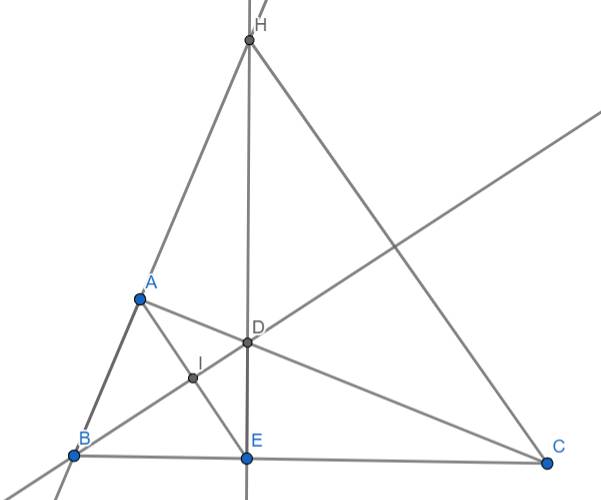
a) Xét hai tam giác vuông ABD (vuông tại A) và tam giác BDE (vuông tại E) ta có: 

BD là cạnh chung 

\(\widehat{ABD}=\widehat{DBE}\) (BD là phân giác của góc B) 

\(\Rightarrow\Delta ABD=\Delta DBE\) (cạnh huyền góc nhọn) 

\(\Rightarrow AB=BE\) (hai cạnh tương ứng) 

b) Ta có: \(\Delta ABD=\Delta DBE\left(cmt\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{ADI}=\widehat{IDE}\\AD=DE\end{matrix}\right.\) 

Xét hai tam giác ADI và tam giác EDI có:

\(\widehat{ADI}=\widehat{IDE}\left(cmt\right)\) 

\(AD=DE\left(cmt\right)\)

\(ID\) là cạnh chung 

\(\Rightarrow\Delta ADI=\Delta EDI\) (c.g.c) 

\(\Rightarrow\widehat{AID}=\widehat{DIE}\) (2 cạnh t.ứng) 

Mà: \(\widehat{ADI}+\widehat{DIE}=180^o\) (kề bù) 

\(\Rightarrow\widehat{ADI}=\widehat{DIE}=\dfrac{180^o}{2}=90^o\)

Hay AE ⊥ BD 

c) Xét 2 tam giác vuông HBE (vuông tại E) và tam giác CBA (vuông tại A) ta có:

\(\widehat{HBC}\) chung 

\(AB=BE\left(cmt\right)\) 

\(\Rightarrow\Delta HBE=\Delta CBA\left(g.c.g\right)\) 

\(\Rightarrow BH=BC\) (2 cạnh t.ứng) 

d) Tam giác HBC có HB = HC (cmt) 

\(\Rightarrow\Delta HBC\) cân tại H 

Gọi F là giao điểm của BD và HC ta có: 

BF là tia phân của góc B 

Nên đồng thời BF cũng là đường cao của tam giác HBC 

\(\Rightarrow BF\perp HC\) (1)

Mà: \(BD\perp AE\) hay \(BF\perp AE\left(cmt\right)\) (2)

Từ (1) và (2) ta có: 

AE//HC (đpcm) 

Yêu cầu của đề là gì vậy ?