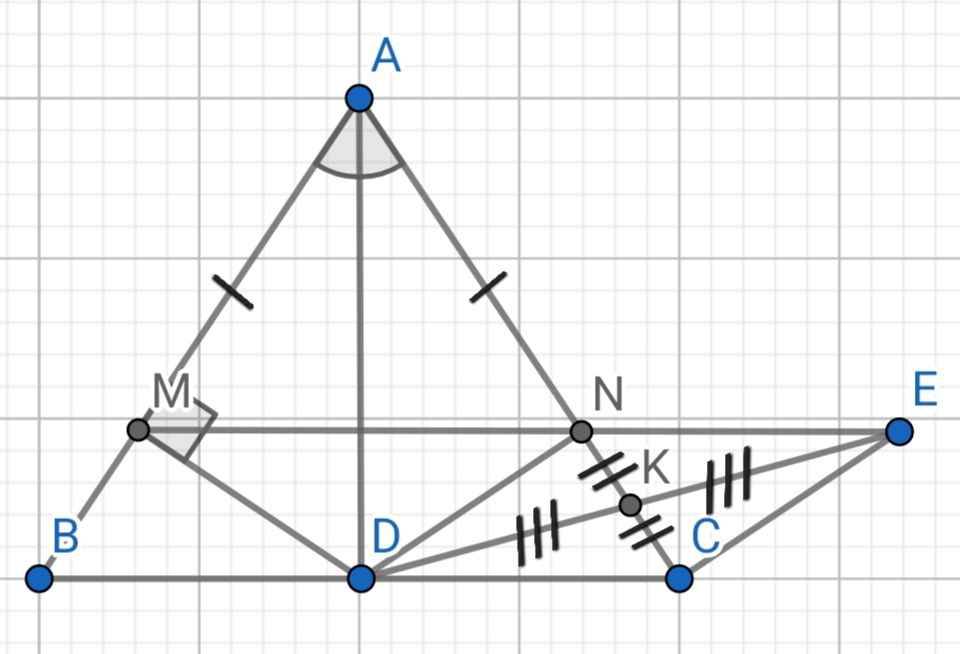
Cho <ABC có AB=AC , AB>BC . Gọi M là trung điểm của BC
a) CMR <ABM=<ACM
b) Trên cạnh AB lấy điểm D , trên cạnh AC lấy điểm E sao cho AD=AE . CMR MD=ME
c) Gọi N là trung điểm của BD . Trên tia đối của tia NM lấy điểm K sao cho NK=NM .CMR DK//BC
d) CMR K;D;E thẳng hàng
Mọi người giúp em giải nhanh trong tối hôm nay với ạ , chỉ cần phần d) thôi ạ . Em cảm ơn mọi người ai giải dc e đánh giá 5 sao và tặng quà ạ