căn của x+2/x^2+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`a)A=x^2+8x+17=x^2+8x+16+1=(x+4)^2+1`
Vì \((x+4)^2 \ge 0 \forall x\)
\(<=>(x+4)^2+1 \ge 1 \forall x\)
Hay \(A \ge 1 \forall x\)
Dấu "`=`" xảy ra `<=>(x+4)^2=0<=>x=-4`
___________________________________________________
\(b)B=x^2-x+4=x^2-2.x. \dfrac{1}{2}+\dfrac{1}{4}+\dfrac{15}{4}=(x+\dfrac{1}{2})^2+\dfrac{15}{4}\)
Vì \((x+\dfrac{1}{2})^2 \ge 0 \forall x<=>(x+\dfrac{1}{2})^2+\dfrac{15}{4} \ge \dfrac{15}{4} \forall x\)
Hay \(B \ge \dfrac{15}{4} \forall x\)
Dấu "`=`" xảy ra \(<=>(x+\dfrac{1}{2})^2=0<=>x=-\dfrac{1}{2}\)

`a)` Với `x > 0,x \ne 1` có:
`A=([\sqrt{x}+2]/[x+2\sqrt{x}+1]-[\sqrt{x}-2]/[x-1]).[\sqrt{x}+1]/\sqrt{x}`
`A=[(\sqrt{x}+2)(\sqrt{x}-1)-(\sqrt{x}-2)(\sqrt{x}+1)]/[(\sqrt{x}+1)^2(\sqrt{x}-1)].[\sqrt{x}+1]/\sqrt{x}`
`A=[x-\sqrt{x}+2\sqrt{x}-2-x-\sqrt{x}+2\sqrt{x}+2]/[\sqrt{x}(\sqrt{x}-1)(\sqrt{x}+1)]`
`A=[2\sqrt{x}]/[\sqrt{x}(x-1)]`
`A=2/[x-1]`
____________________________________________________
`2)A in ZZ<=>2/[x-1] in ZZ`
`=>x-1 in Ư_2`
Mà `Ư_2={+-1;+-2}`
`@x-1=1=>x=2` (t/m)
`@x-1=-1=>x=0` (ko t/m)
`@x-1=2=>x=3` (t/m)
`@x-1=-2=>x=-1` (ko t/m)
Vậy `x in {2;3}`


a) Áp dụng hệ thức giữa cạnh và đường cao vào tam giác ABC vuông tại A , đường cao AH , ta có :
\(BH.HC=AH^2\left(1\right)\)
Áp dụng hệ thức giữa cạnh và đường cao vào tam giác AHB vuông tại H , đường cao HK , ta có :
\(AH^2=AB.AK\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow AB.AK=BH.HC\) ( ĐPCM )
b) Áp dụng hệ thức giữa cạnh và đường cao vào tam giác ABC vuông tại A , đường cao AH , ta có :
\(\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\end{matrix}\right.\)
\(\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}=\dfrac{HB}{HC}\) ( đpcm )

Điều kiện \(x\ge\dfrac{1}{4}\)
Đặt \(\sqrt{4x-1}=p\left(p\ge0\right)\), khi đó pt đã cho trở thành:
\(3x^3+x^2=3p^3+p^2\)
\(\Leftrightarrow\left(3x^3-3p^3\right)+\left(x^2-p^2\right)=0\)
\(\Leftrightarrow\left(x-p\right)\left(3x^2+3xp+3p^2\right)+\left(x-p\right)\left(x+p\right)=0\)
\(\Leftrightarrow\left(x-p\right)\left(3x^2+3xp+3p^2+x+p\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=p\\3x^2+3xp+3p^2+x+p=0\end{matrix}\right.\)
Xét TH \(x=p\) \(\Leftrightarrow x=\sqrt{4x-1}\) \(\Rightarrow x^2=4x-1\) \(\Leftrightarrow x^2-4x+1=0\) (*)
Đến đây ta thấy \(\Delta'=\left(-2\right)^2-1.1=3>0\) nên pt (*) luôn có 2 nghiệm phân biệt \(x_1,x_2\):
\(x_1=\dfrac{-\left(-2\right)+\sqrt{3}}{1}=2+\sqrt{3}\) (nhận)
\(x_2=\dfrac{-\left(-2\right)-\sqrt{3}}{1}=2-\sqrt{3}\) (nhận)
Khi đó, theo hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=1\end{matrix}\right.\)
Mà tổng bình phương các nghiệm của pt đã cho chính bằng \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4^2-2.1=14\)
Ta xét tiếp trường hợp \(3x^2+3xp+3p^2+x+p=0\)
(Theo mình thì trường hợp này chắc vô nghiệm)
Vậy tổng bình phương các nghiệm của pt đã cho bằng 14.
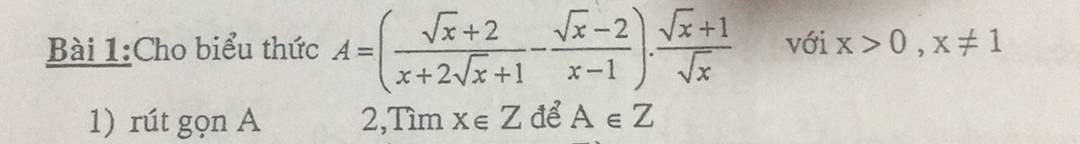

ĐK của căn thức là `[x+2]/[x^2+1] >= 0`
Mà `x^2+1 > 0`
`=>x+2 >= 0`
`<=>x >= -2`
ĐK của căn thức là \(\dfrac{x+2}{x^2+1} \ge 0\)
Mà `x^2+1 > 0`
\(=>x+2 \ge 0\)
\(<=>x \ge -2\)