x mũ n nhân y mũ n +2 nhân (xy+x mũ 2 y +1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`@` `\text {Ans}`
`\downarrow`
`1.`
`3x^2y - 7x^2y + 5x^2y`
`= (3 - 7 + 5)x^2y`
`= x^2y`
`2.`
`-7x^3y^4 + 4x^3y^4 - 2x^3y^4`
`= (-7+4-2) x^3y^4`
`= -5x^3y^4`
`3.`
`4xy^5 - 8xy^5 + 4xy^5`
`= (4 - 8 + 4) xy^5`
`= 0xy^5`
`= 0`
`4.`
`5x^5y^7 - 8x^5y^7 - 2x^5y^7`
`= (5 - 8 - 2) x^5y^7`
`= -5x^5y^7`
`5.`
`9x^2y^5 - 12x^2y^5 + x^2y^5`
`= (9 - 12 + 1)x^2y^5`
`= -2x^2y^5`

`@` `\text {Ans}`
`\downarrow`
\((x+y)(x-y)+(xy^4-x^3y^2) \div (xy^2) \)
`= x(x-y) + y(x-y) + xy^4 \div xy^2 - x^3y^2 \div xy^2`
`= x^2 - xy + xy - y^2 + y^2 - x^2`
`= (x^2 - x^2) + (-xy + xy) + (-y^2 + y^2)`
`= 0`

Bài 2
1) Thay x = 1 vào A ta được:
A = 3.1² - 7.1 + 5 = 3 - 7 + 5 = 1
2) Thay x = -1 và y = 2 vào B ta được:
B = 5.(-1)² - 4.(-1).2 + 7
= 5 + 8 + 7
= 20
3) Thay x = 3 và y = 2 vào C ta được:
C = (3 - 2)² + 2.3 - 2
= 1 + 6 - 2
= 5
5) Thay x = 4 vào D ta được:
D = 3.4² - 4 + 5
= 3.16 - 4 + 5
= 48 - 4 + 5
= 49
5) Thay x = 1 và y = -1 vào E ta được:
E = 3,2.1⁵.(-1)³ = 3,2.1.(-1) = -3,2

\(6xy\left(xy-y^2\right)-8x^2\left(x-y^2\right)+5y^2\left(x^2+xy\right)\\ =6x^2y^2-6xy^3-8x^3+8x^2y^2+5x^2y^2+5xy^3\\ =\left(6x^2y^2+8x^2y^2+5x^2y^2\right)+\left(-6xy^3+5xy^3\right)-8x^3\\ =19x^2y^2-xy^3-8x^3\)
Với `x=1/2;y=2` ta có :
\(19x^2y^2-xy^3-8x^3\\ =19.\left(\dfrac{1}{2}\right)^2.2^2-\dfrac{1}{2}.2^3-8.2^3\\ =19.\dfrac{1}{4}.4-\dfrac{1}{2}.8-8.8\\ =19-4-64\\ =-49\)

`@` `\text {Ans}`
`\downarrow`
`1,`
`-` Đơn thức là biểu thức đại số gồm 1 số, 1 biến hoặc là tích của biến và 1 số thực
`=>` Đơn thức trong các biểu thức đại số trên là C.
`2,`
`-` Hệ số của đơn thức `7x^3y^2` là `7`
`=> A.`
`3,`
`-` Số `0` cũng là đơn thức, được gọi là đơn thức bậc `0`
`=> A.`
`4,`
`-` Phần hệ số của đơn thức `-3/5 x^4y^3` là `-3/5`
`=> B.`
`5,`
\(-5x^4y^5(-2)xy(3)\)
`= [ (-5)*(-2)*3]*(x^4*x)*(y^5*y)`
`= 30x^5y^6`
`=> C.`

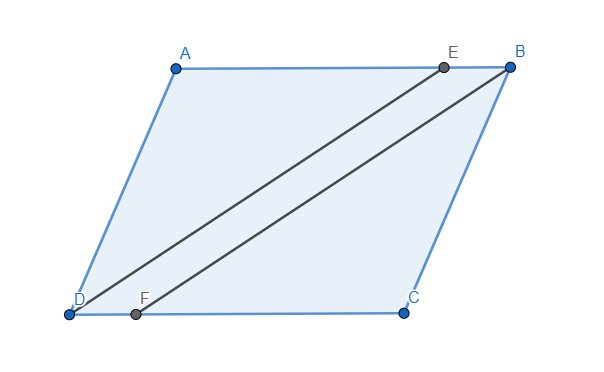
a) Ta thấy \(\widehat{AED}=\widehat{EDC}=\widehat{ADE}\) nên tam giác ADE cân tại A. Hoàn toàn tương tự thì tam giác CBF cân tại C.
Mặt khác, do tứ giác ABCD là hình bình hành nên \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\). Do đó \(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{D}}{2}\) hay \(\widehat{CBF}=\widehat{ADE}\). Kết hợp với \(\widehat{A}=\widehat{C}\) thì suy ra \(\Delta ADE~\Delta CBF\left(g.g\right)\). Lại có \(\dfrac{AD}{CB}=1\) (do tứ giác ABCD là hình bình hành), suy ra \(\Delta ADE=\Delta CBF\) (2 tam giác đồng dạng có tỉ số đồng dạng bằng 1 thì 2 tam giác đó bằng nhau), ta có đpcm.
b) Ta thấy \(\widehat{AED}=\widehat{ADE}=\widehat{CBF}=\widehat{ABF}\) nên DE//BF. Lại có BE//DF (do tứ giác ABCD là hình bình hành) nên tứ giác DEBF cũng là hình bình hành (các cặp cạnh đối song song).
a/
Xét tg ADE có
\(\widehat{ADE}=\widehat{CDE}\) (gt) (1)
\(\widehat{AED}=\widehat{CDE}\) (góc so le trong) (1)
Từ (1) và (2) => \(\widehat{ADE}=\widehat{AED}\) => tg ADE là tg cân tại A
=> AD=AE (3)
Xét tg CBF có
\(\widehat{CBF}=\widehat{ABF}\) (gt) (4)
\(\widehat{CFB}=\widehat{ABF}\) (góc so le trong) (5)
Từ (4) và (5) => \(\widehat{CBF}=\widehat{CFB}\) => tg CBF cân tại C
=> CB=CF (6)
Ta có
AD=CB (cạnh đối hình bình hành) (7)
Từ (3) (6) (7) => AD=AE=CB=CF
Mà \(\widehat{DAE}=\widehat{BCF}\) (góc đối hình bình hành)
=> tg ADE = tg CBF (c.g.c)
=> tg ADE và tg CBF là những tg cân bằng nhau
b/
tg ADE = tg CBF (cmt) \(\Rightarrow\widehat{BFC}=\widehat{ADE}\)
Mà \(\widehat{EDC}=\widehat{ADE}\) (gt)
\(\Rightarrow\widehat{BFC}=\widehat{EDC}\) Hai góc này ở vị trí đồng vị => DE//BF (8)
Ta có
AB//CD (cạnh đối hình bình hành) => BE//DF (9)
Từ (8) (9) => DEBF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hình bình hành)

a. 3xy( 4x + y - \(\dfrac{4}{3}\) )
b. 2x2( 3x + 1 )
c. (2x + 3 )( x - y )
d. xy( 1 - x )( x - 1 )
e. 6( 2x + 1 )( x + y )
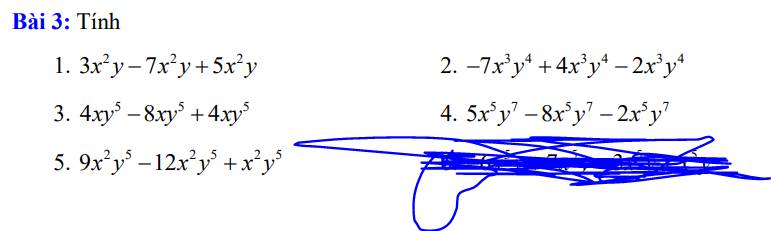


Bài yêu cầu gì em?