tìm nghiệm của các đa thức:
h(x)=x2+5x+6
g(x)=2x2+7x-9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1+1/2.(1+2)+1/3.(1+2+3)+1/4.(1+2+3+4)+...+1/2023.(1+2+3+...+2023)
=1+1/2.(1+2).2/2+1/3.(1+3).3/2+1/4.(1+4).4/2+...+1/2023.(1+2+3+...+2023).2023/2
=2/2+3/2+4/2+...+2023/2
=2+3+4+...+2023/2
=2025.2022/2/2
=1023637,5
tham khảo thôi nha

Lời giải:
BĐT $\Leftrightarrow abc\geq (a+b-c)(b+c-a)(c+a-b)(*)$
Áp dụng BĐT AM-GM:
$(a+b-c)(b+c-a)\leq \left(\frac{a+b-c+b+c-a}{2}\right)^2=b^2$
$(b+c-a)(c+a-b)\leq \left(\frac{b+c-a+c+a-b}{2}\right)^2=c^2$
$(a+b-c)(a+c-b)\leq \left(\frac{a+b-c+a+c-b}{2}\right)^2=a^2$
Nhân theo vế 3 BĐT trên:
$[(a+b-c)(b+c-a)(c+a-b)]^2\geq (abc)^2$
$\Rightarrow abc\geq (a+b-c)(b+c-a)(c+a-b)$ (BĐT $(*)$ được cm)
Ta có đpcm.

Đổi 1 giờ 30 phút = 1,5 giờ
Tỉ số gian người đi xe máy trên cả quãng đường so với thời gian người đi xe đạp trên cả quãng đường là:
1 : 3 = \(\dfrac{1}{3}\)
Theo bài ra ta có sơ đồ:
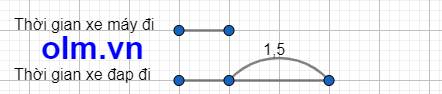
Theo sơ đồ ta có:
Thời gian người đó đi xe đạp trên cả quãng đường AB là:
1,5 : ( 3 - 1) \(\times\) 3 = 2,25 giờ
Vận tốc của xe đạp khi đi trên quãng đường AB là:
36 : 2,25 = 16 (km/h)
Vận tốc của xe máy là: 16 \(\times\) 3 = 48 (km/h)
Đáp số: vận tốc xe máy 48 km/h
vận tốc xe đạp 16 km/h

P = \(\dfrac{-3x}{x+4}\)
P \(\in\) Z ⇔ -3\(x\) ⋮ \(x+4\) ⇒ -3( \(x\) +4) +12 ⋮ \(x+4\)
⇒ 12 ⋮ \(x\) + 4
⇒ \(x\) + 4 \(\in\) { -12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6}
\(\Rightarrow\) \(x\) \(\in\) { -16; -10; -8; -7; -6; -5; -3; -2; -1; 0; 2}

Lời giải:
Áp dụng BĐT AM-GM ta có:
$\frac{a^2}{4}+b^2\geq 2\sqrt{\frac{a^2}{4}.b^2}=ab$
$\frac{a^2}{4}+c^2\geq ac$
$\frac{a^2}{4}+x^2\geq ax$
$\frac{a^2}{4}+y^2\geq ay$
Cộng theo vế các BĐT trên ta có:
$a^2+b^2+c^2+x^2+y^2\geq ab+ac+ax+ay=a(b+c+x+y)$ (đpcm)
Phân tích đa thức thành nhân tử thôi bạn :
Ta có :
\(h\left(x\right)=x^2+5x+6\)
\(h\left(x\right)=x\left(x+2\right)+3\left(x+2\right)\)
\(h\left(x\right)=\left(x+2\right)\left(x+3\right)\)
\(\Rightarrow N_oh\left(x\right)=-2;-3\)
\(g\left(x\right)=2x^2+7x-9\)
\(g\left(x\right)=2x^2+9x-2x-9\)
\(g\left(x\right)=2x\left(x-1\right)+9\left(x-1\right)\)
\(g\left(x\right)=\left(x-1\right)\left(2x+9\right)\)
\(\Rightarrow N_og\left(x\right)=1;-4,5\)
ko biet