chu vi tam giâc là: 48 : 2  = 24(cm)

Độ dài ba cạnh lần lượt là: a; b; c (cm)

       Theo bài ra ta có: \(\dfrac{a}{21}=\dfrac{b}{28}=\dfrac{c}{35}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

              \(\dfrac{a}{21}\) = \(\dfrac{b}{28}\) = \(\dfrac{c}{35}\) = \(\dfrac{a+b+c}{21+28+35}\) = \(\dfrac{24}{84}\) =\(\dfrac{2}{7}\)

                a = 21 x \(\dfrac{2}{7}\) = 3

               b = 28 x \(\dfrac{2}{7}\) = 8

               \(c\) = 35 \(\times\) \(\dfrac{2}{7}\) = 10

Vậy độ dài ba cạnh lần lượt là: 3 cm; 8cm ; 10 cm 

Độ dài đường chéo HCN:

\(\sqrt{10^2+7^2}=\sqrt{100+49}=\sqrt{149}\approx12,21\left(cm\right)\)

cảm ơn các bạn

nhầm

tớ nhắn lộn hihi

lên google mà tim câu trả lời

4 - x = -(x - 4) = -(x  + 1 - 5)

= -(x + 1) + 5

Để (4 - x) ⋮ (x + 1) thì 5 ⋮ (x + 1)

⇒ x + 1 ∈ Ư(5) = {-5; -1; 1; 5}

⇒ x ∈ {-6; -2; 0; 4}

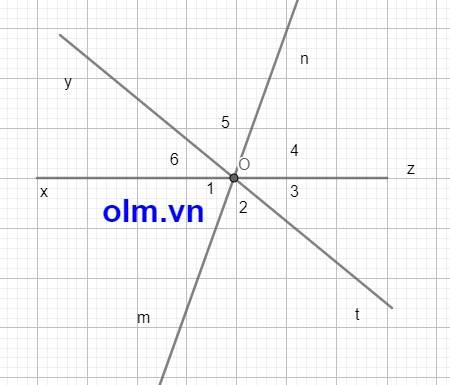
Vì góc yOz và góc xOy là hai góc kề bù nên Oz và Ox cùng nằm trên một đường thẳng zx (1) 

Tương tự ta có: Ot và Oy cùng nằm trên một đường thẳng

\(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh

⇒ \(\widehat{O_2}\) = \(\dfrac{1}{2}\) \(\widehat{xOt}\) = \(\dfrac{1}{2}\) \(\widehat{yOz}\) = \(\widehat{O_5}\)

Mặt khác ta có: \(\widehat{O_2}\) + \(\widehat{O_1}\) + \(\widehat{O_6}\) = 180⁰ (gt)

                     ⇒ \(\widehat{O_1}\) + \(\widehat{O_6}\) + \(\widehat{O_5}\) ₌ 180⁰ 

                    ⇒ Om và On cùng thuộc một đường thẳng mn (2)

Kết hợp (1) và (2) ta có:   góc zOn và góc xOm là hai góc đối đỉnh