số học sinh của lớp 9A nhiều hơn số học sinh của lớp 9B là 10 học sinh trong đợt lao động trồng cây mỗi học sinh lớp 9A trồng được 3 cây học sinh lớp 9B trồng được 4 cây tìm số học sinh mỗi lớp biết tổng số của 2 lớp là 275 cây
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ giả thiết \(\Rightarrow a+b=abc-c=c\left(ab-1\right)\Rightarrow c=\dfrac{a+b}{ab-1}\) (hiển nhiên \(ab-1>0\) do \(a+b>0\))
Đặt \(P=\dfrac{\sqrt{1+a^2}}{a}+\dfrac{\sqrt{1+b^2}}{b}-\sqrt{1+c^2}\)
\(=\dfrac{\sqrt{1+a^2}}{a}+\dfrac{\sqrt{1+b^2}}{b}-\sqrt{1+\left(\dfrac{a+b}{ab-1}\right)^2}\)
\(=\dfrac{\sqrt{1+a^2}}{a}+\dfrac{\sqrt{1+b^2}}{b}-\dfrac{\sqrt{\left(a^2+1\right)\left(b^2+1\right)}}{ab-1}\)
\(\Rightarrow P< \dfrac{\sqrt{1+a^2}}{a}+\dfrac{\sqrt{1+b^2}}{b}-\dfrac{\sqrt{\left(a^2+1\right)\left(b^2+1\right)}}{ab}\)
Đặt \(\left\{{}\begin{matrix}\dfrac{\sqrt{1+a^2}}{a}=\sqrt{1+\dfrac{1}{a^2}}=x>1\\\dfrac{\sqrt{1+b^2}}{b}=\sqrt{1+\dfrac{1}{b^2}}=y>1\end{matrix}\right.\)
\(\Rightarrow P< x+y-xy=x+y-xy-1+1=\left(x-1\right)\left(1-y\right)+1\)
Do \(x>1;y>1\Rightarrow\left(x-1\right)\left(1-y\right)< 0\Rightarrow P< 1\)

\(B=\sqrt{\dfrac{8+\sqrt{15}}{2}}+\sqrt{\dfrac{8-\sqrt{15}}{2}}\)
\(B=\dfrac{\sqrt{8+\sqrt{15}}}{\sqrt{2}}+\dfrac{\sqrt{8-\sqrt{15}}}{\sqrt{2}}\)
\(B=\dfrac{\sqrt{2}\cdot\sqrt{8+\sqrt{15}}}{\sqrt{2}\cdot\sqrt{2}}+\dfrac{\sqrt{2}\cdot\sqrt{8-\sqrt{15}}}{\sqrt{2}\cdot\sqrt{2}}\)
\(B=\dfrac{\sqrt{16+2\sqrt{15}}}{2}+\dfrac{\sqrt{16-2\sqrt{15}}}{2}\)
\(B=\dfrac{\sqrt{\left(\sqrt{15}\right)^2+2\cdot\sqrt{15}\cdot1+1^2}}{2}+\dfrac{\sqrt{\left(\sqrt{15}\right)^2-2\cdot\sqrt{15}\cdot1+1^2}}{2}\)
\(B=\dfrac{\sqrt{\left(\sqrt{15}+1\right)^2}}{2}+\dfrac{\sqrt{\left(\sqrt{15}-1\right)^2}}{2}\)
\(B=\dfrac{\sqrt{15}+1+\sqrt{15}-1}{2}\)
\(B=\dfrac{2\sqrt{15}}{2}\)
\(B=\sqrt{15}\)

ta có P(1)=1+a+b+c+d+e=3
P(2)=32+16a+8b+4c+2d+e=9
P(3)=243+81a+27b+9c+3d+e=19
P(4)=1024+256a+64b+16c+4d+e=33
P(5)=3125+625a+125b+25c+5d+e=51
<=> P(1)=a+b+c+d+e=2
P(2)=16a+8b+4c+2d+e=-23
P(3)=81a+27b+9c+3d+e=-224
P(4)=256a+64b+16c+4d+e=-991
P(5)=625a+125b+25c+5d+e=-3074
<=> 15a+7b+3c+d=-25
65a+19b+5c+d=-201
175a+37b+7c+d=-767
369a+61b+9c+d=-2083
<=> a=-15
b=85
c=-223
d=274
Nên e=-119
Vậy P(x)= x5-15x4+85x3-223x2+274x-119
=> P(6)=193
P(7)=819
P(8)=2649
P(9)=6883
P(10)=15321
P(11)=30483

\(x^2+3x+2+2\left(2-x\right)\sqrt{x-1}=0\left(x\ge1\right)\)
\(\Leftrightarrow x^2-x-2x+2-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-2\right)\sqrt{x-1}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x-1}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x-1=0\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=1\left(tm\right)\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=5\end{matrix}\right.\left(tm\right)\)
Vậy: \(x\in\left\{1;2;5\right\}\)

Đặt \(\left\{{}\begin{matrix}\sqrt[3]{x}=a\\\sqrt[3]{y}=b\end{matrix}\right.\) hệ trở thành \(\left\{{}\begin{matrix}2\left(a^3+b^3\right)=3\left(a^2b+ab^2\right)\\a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left[\left(a+b\right)^3-3ab\left(a+b\right)\right]=3ab\left(a+b\right)\\a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(6^3-18ab\right)=18ab\\a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}ab=8\\a+b=6\end{matrix}\right.\)
\(\Rightarrow\) a và b là nghiệm của \(t^2-6t+8=0\Rightarrow\left[{}\begin{matrix}t=4\\t=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=4;b=2\\a=2;b=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=64;y=8\\x=8;y=64\end{matrix}\right.\)
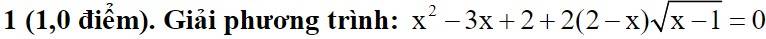
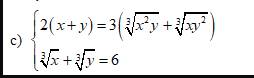
Gọi số học sinh lớp 9B là : \(x\) (học sinh) \(\left(x\inℕ^∗\right)\)
\(\Rightarrow\) Số học sinh lớp 9A là : \(x+10\) (học sinh)
Số cây học sinh lớp 9B trồng được : \(4x\) (cây)
Số cây học sinh lớp 9A trồng được : \(3\left(x+10\right)\) (cây)
Vì tổng số cây 2 lớp trồng được là : 275 cây
Nên ta có pt :
\(3\left(x+10\right)+4x=275\\ \Rightarrow3x+30+4x=275\\ \Rightarrow7x=245\\ \Rightarrow x=35\left(TMDK\right)\)
Vậy số HS lớp 9B là : 35 HS và lớp 9A là : 35+10=45(HS)
HS lớp 9B là 35hs. HS lớp 9A là 45hs.