(x-1)^2=5^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau 1 năm số tiền nhận được là:
\(100\cdot\left(1+7,2\%\right)=107,2\)(triệu đồng)
Sau 2 năm số tiền nhận được là:
\(107,2\cdot\left(1+7,2\%\right)=114,9184\)(triệu đồng)

\(M=\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right).....\left(100-50^2\right)\\ =\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right).....\left(100-10^2\right).....\left(100-50^2\right)\\ =\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right).....\left(100-100\right).....\left(100-50^2\right)\\ =\left(100-1\right)\left(100-2^2\right)\left(100-3^2\right)....0....\left(100-50^2\right)=0\)

Khối lượng nước trong cơ thể là:
\(60\cdot70\%=42\left(kg\right)\)

\(48+\left(225:15+3\times X+7\right)=58\)
=>\(48+\left(15+7+3\times X\right)=58\)
=>\(3\times X=58-48-15-7=10-15-7=-12\)
=>\(X=-12:3=-4\)

Tỉ số giữa số học sinh nữ với tổng số học sinh là:
\(\dfrac{30}{48}=\dfrac{30:6}{48:6}=\dfrac{5}{8}\)

Câu 1: Diện tích nền nhà là:
\(4,2\cdot20,5=86,1\left(m^2\right)\)

Câu 1:
\(-9\%=-\dfrac{9}{100}=-0,09\)
\(59\%=\dfrac{59}{100}=0,59\)
\(-542\%=-\dfrac{542}{100}=-5,42\)
Câu 10:
\(0,68=\dfrac{68}{100}=68\%\)
\(-0,02=-\dfrac{2}{100}=-2\%\)
\(-2,36=-\dfrac{236}{100}=-236\%\)

a: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\) và \(MA\cdot MB=HM^2\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right);NA\cdot NC=NH^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\left(3\right);AB^2=BH\cdot BC;AC^2=CH\cdot BC\)
Từ (1) và (3) suy ra \(AM\cdot AB=HB\cdot HC\)
b: Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>\(HA^2=HM^2+HN^2\)
=>\(HB\cdot HC=MA\cdot MB+NA\cdot NC\)
d: \(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)
=>\(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
e: Xét ΔAHB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM=\dfrac{BH^2}{BA}\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(CN\cdot CA=CH^2\)
=>\(CN=\dfrac{CH^2}{CA}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(BC=\dfrac{AB\cdot AC}{AH}\)
\(BM\cdot CN\cdot BC=\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{CA}\cdot\dfrac{AB\cdot AC}{AH}\)
\(=\dfrac{BH^2}{AH}\cdot CH^2=\dfrac{\left(BH\cdot CH\right)^2}{AH}=\dfrac{AH^4}{AH}=AH^3\)
mà AH=MN(AMHN là hình chữ nhật)
nên \(BM\cdot CN\cdot BC=MN^3\)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
b: DA=DE
=>D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
mà BD cắt AE tại F
nên F là trung điểm của AE
=>CF là đường trung tuyến của ΔAEC
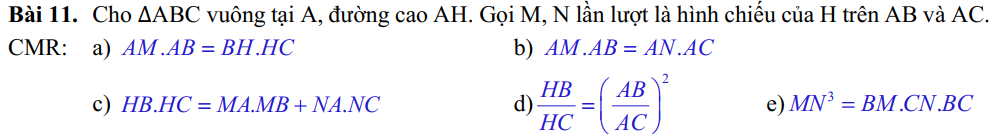
\(\left(x-1\right)^2=5^2\)
=>\(\left[{}\begin{matrix}x-1=5\\x-1=-5\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1+5=6\\x=-5+1=-4\end{matrix}\right.\)