
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi đơn vị: 27km/h= \(\dfrac{27000}{3600}\)km/s = 7,5 km/s
1 phút 15 giây = 75 giây
Quãng đường tàu hỏa đi được: s = vt=7,5 x 75 = 562,5 m
Chiều dài toa tàu: L = 562.5 - 85 = 477,5 m

a: \(\left\{{}\begin{matrix}x-y=2\\3x+4y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+2\\3\left(y+2\right)+4y=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=y+2\\3y+6+4y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=14\\x=y+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2\\x=y+2=2+2=4\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}4x-2y=1\\-2x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-2y=1\\y=2x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x\\4x-2\cdot2x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x\\0x=1\left(vôlý\right)\end{matrix}\right.\)
vậy: Hệ vô nghiệm
c: \(\left\{{}\begin{matrix}\dfrac{x}{3}+\dfrac{y}{4}=4\\x+y-14=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=48\\x+y=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=14-y\\4\left(14-y\right)+3y=48\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=14-y\\56-4y+3y=48\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}56-y=48\\x=14-y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=56-48=8\\x=14-8=6\end{matrix}\right.\)


a: Thay x=2 và y=0 vào -2x+5y=7, ta được:
\(-2\cdot2+5\cdot0=7\)
=>-4+0=7(vô lý)
=>Loại
Thay x=-1 và y=1 vào -2x+5y=7, ta được:
\(-2\cdot\left(-1\right)+5\cdot1=7\)
=>2+5=7
=>7=7(nhận)
=>Nhận
Thay x=-1 và y=6 vào -2x+5y=7, ta được:
\(\left(-2\right)\cdot\left(-1\right)+5\cdot6=7\)
=>2+30=7
=>32=7(loại)
=>Loại
Thay x=4 và y=3 vào -2x+5y=7, ta được:
\(-2\cdot4+5\cdot3=7\)
=>-8+15=7
=>7=7(đúng)
=>Nhận
Thay x=-2 và y=-5 vào -2x+5y=7, ta được:
\(-2\cdot\left(-2\right)+5\cdot\left(-5\right)=7\)
=>4-25=7
=>-21=7(sai)
=>Loại
Thay x=2 và y=0 vào 4x-3y=7, ta được:
\(4\cdot2-3\cdot0=7\)
=>8=7(sai)
=>Loại
Thay x=-1 và y=1 vào 4x-3y=7, ta được:
\(4\cdot\left(-1\right)-3\cdot1=7\)
=>-7=7(sai)
=>Loại
Thay x=-1 và y=6 vào 4x-3y=7, ta được:
\(4\cdot\left(-1\right)-3\cdot6=7\)
=>-4-18=7
=>-22=7(sai)
=>Loại
Thay x=4 và y=3 vào 4x-3y=7, ta được:
\(4\cdot4-3\cdot3=7\)
=>16-9=7(đúng)
=>Nhận
Thay x=-2 và y=-5 vào 4x-3y=7, ta được:
\(4\left(-2\right)-3\cdot\left(-5\right)=7\)
=>-8+15=7
=>7=7(đúng)
=>Nhận
Vậy: Các cặp số là nghiệm của (1) là (-1;1);(4;3)
Các cặp số là nghiệm của (2) là (-2;-5); (4;3)
b: Cặp số là nghiệm của của 2 phương trình (1),(2) là (4;3)

1: \(\left(x+1\right)^2=x^2+2\cdot x\cdot1+1^2=x^2+2x+1\)
2: \(\left(4+x\right)^2=4^2+2\cdot4\cdot x+x^2=16+8x+x^2\)
5: \(\left(5x+1\right)^2=\left(5x\right)^2+2\cdot5x\cdot1+1^2=25x^2+10x+1\)
6: \(\left(2x+3\right)^2=\left(2x\right)^2+2\cdot2x\cdot3+3^2=4x^2+12x+9\)
9: \(\left(x+2y\right)^2=x^2+2\cdot x\cdot2y+\left(2y\right)^2=x^2+4xy+4y^2\)
10: \(\left(x+5y\right)^2=x^2+2\cdot x\cdot5y+\left(5y\right)^2=x^2+10xy+25y^2\)
13: \(\left(3x+5y\right)^2=\left(3x\right)^2+2\cdot3x\cdot5y+\left(5y\right)^2\)
\(=9x^2+30xy+25y^2\)
14: \(\left(2x+3y\right)^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=4x^2+12xy+9y^2\)
17: \(\left(x^2+9\right)^2=\left(x^2\right)^2+2\cdot x^2\cdot9+9^2=x^4+18x^2+81\)
18: \(\left(2x^2+1\right)^2=\left(2x^2\right)^2+2\cdot2x^2\cdot1+1^2=4x^4+4x^2+1\)
21: \(\left(x+2y^2\right)^2=x^2+2\cdot x\cdot2y^2+\left(2y^2\right)^2=x^2+4xy^2+4y^4\)
22: \(\left(2x+3y^2\right)^2\)
\(=\left(2x\right)^2+2\cdot2x\cdot3y^2+\left(3y^2\right)^2\)
\(=4x^2+12xy^2+9y^4\)

\(\left\{{}\begin{matrix}x-3y=-2\\2x+3y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-3y+2x+3y=-2+2\\x-3y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=0\\3y=x-\left(-2\right)=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\3y=0+2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{2}{3}\end{matrix}\right.\)
Vậy: Cặp số (0;2/3) là nghiệm của hệ phương trình, còn hai cặp số (0;1); (4;5) không là nghiệm của hệ phương trình

6h40p=20/3 giờ
Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là a(giờ) và b(giờ)
(Điều kiện: a>0; b>0)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{a}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{b}\)(công việc)
Trong 1 giờ, hai người làm được: \(1:\dfrac{20}{3}=\dfrac{3}{20}\)(công việc)
Do đó, ta có: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\left(1\right)\)
Trong 5 giờ, người thứ nhất làm được: \(\dfrac{5}{a}\)(công việc)
Trong 8 giờ, người thứ hai làm được: \(\dfrac{8}{b}\)(công việc)
Nếu người thứ nhất làm trong 5 giờ, sau đó nghỉ và người thứ hai làm trong 8 giờ thì xong nên ta có: \(\dfrac{5}{a}+\dfrac{8}{b}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\\\dfrac{5}{a}+\dfrac{8}{b}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{a}+\dfrac{5}{b}=\dfrac{3}{4}\\\dfrac{5}{a}+\dfrac{8}{b}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{a}+\dfrac{8}{b}-\dfrac{5}{a}-\dfrac{5}{b}=1-\dfrac{3}{4}\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{b}=\dfrac{1}{4}\\\dfrac{1}{a}=\dfrac{3}{20}-\dfrac{1}{b}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12\\\dfrac{1}{a}=\dfrac{3}{20}-\dfrac{1}{12}=\dfrac{9}{60}-\dfrac{5}{60}=\dfrac{4}{60}=\dfrac{1}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=12\\a=15\end{matrix}\right.\left(nhận\right)\)
Vậy: thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là 15(giờ) và 12(giờ)
Gọi thời gian nếu làm riêng của người thứ nhất, người thứ hai để hoàn thành công việc lần lượt là $a,b$ (giờ; $a,b>0$)
Mỗi giờ người thứ nhất làm được: $\frac1a$ (công việc)
Mỗi giờ người thứ hai làm được: $\frac1b$ (công việc)
Vì hai người cùng làm việc thì trong 6 giờ 40 phút (= $\frac{20}{3}$ giờ) thì xong công việc nên ta có phương trình: $\frac{20}{3}(\frac 1a+\frac1b)=1$
$\Leftrightarrow \frac1a+\frac1b=\frac{3}{20}$ (1)
Vì nếu người thứ nhất làm riêng trong 5 giờ rồi người thứ hai tiếp tục làm nốt trong 8 giờ thì xong công việc nên ta có phương trình:
$\frac5a+\frac8b=1$ (2)
Từ (1) và (2) ta có hệ: $\begin{cases} \frac1a+\frac1b=\frac{3}{20} \\ \frac5a+\frac8b=1 \end{cases}$
Đặt $\frac 1a=u:\frac1b=v;(u,v>0)$
Khi đó hot trở thành: $\begin{cases} u+v=\frac{3}{20}\\ 5u+8v=1\end{cases} \Leftrightarrow \begin{cases} u=\frac{1}{15}\\v=\frac{1}{12}\end{cases}$
$\Rightarrow \begin{cases} \frac1a=\frac{1}{15}\\\frac1b=\frac{1}{12} \end{cases} \Rightarrow \begin{cases} a=15 (tm)\\b=12(tm) \end{cases}$
Vậy: ...
#$\mathtt{Toru}$

100-(2,6+23,4:6)x10,8
=100-(2,6+3,9)x10,8
=100-10,8x6,5
=100-70,2
=29,8

32,5x4,5+32,5x5,4+3,25
=32,5x(4,5+5,4)+32,5x0,1
=32,5x9,9+32,5x0,1
=32,5x10=325
32,5 x 4,5 + 32,5 x 5,4 + 3,25
= 32,5 x 4,5 + 32,5 x 5,4 + 32,5 x 0,1
= 32,5 x ( 4,5 + 5,4 + 0,1 )
= 32,5 x 10
= 325
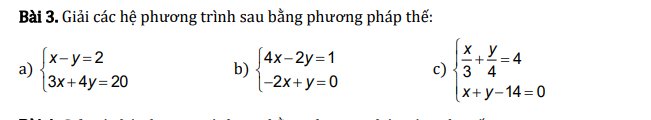




a: \(\left\{{}\begin{matrix}x-3y=4\\2x+3y=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3y+2x+3y=4+17\\x-3y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=21\\3y=x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\3y=7-4=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}2x+5y=8\\2x-7y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+5y-2x+7y=8-0\\2x=7y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12y=8\\x=\dfrac{7}{2}y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{8}{12}=\dfrac{2}{3}\\x=\dfrac{7}{2}\cdot\dfrac{2}{3}=\dfrac{7}{3}\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}3x+5y=14\\-4x+3y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x+20y=56\\-12x+9y=60\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x+20y-12x+9y=56+60\\3x+5y=14\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}29y=116\\3x=14-5y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\3x=14-5\cdot4=14-20=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=4\\x=-2\end{matrix}\right.\)