Đặt \(A=2+2^3+...+2^{2023}\)

=>\(4A=2^3+2^5+2^7+...+2^{2025}\)

=>\(4A-A=2^3+2^5+...+2^{2025}-2-2^3-...-2^{2023}\)

=>\(3A=2^{2025}-2\)

=>\(A=\dfrac{2^{2025}-2}{3}\)

Diện tích xung quanh căn phòng là:

\(\left(8+5\right)\cdot2\cdot4=13\cdot8=104\left(m^2\right)\)

Diện tích không cần quét vôi là:

\(2,2\cdot1,2\cdot2+1,4\cdot0,8\cdot4=9,76\left(m^2\right)\)

Diện tích cần quét vôi là:

\(104+8\cdot5-9,76=134,24\left(m^2\right)\)

Số tiền cần phải trả là:

\(134,24\cdot10000=1342400\left(đồng\right)\)

Cảm ơn bạn rất nhiều!

Diện tích đáy là \(5\cdot\dfrac{2}{2}=5\left(cm^2\right)\)

Thể tích của hình lăng trụ là: \(4\cdot5=20\left(cm^3\right)\)

Đặt \(A=3^0+3^1+...+3^{100}\)

=>\(3A=3+3^2+...+3^{101}\)

=>\(3A-A=3+3^2+...+3^{101}-1-3^1-...-3^{100}\)

=>\(2A=3^{101}-1\)

=>\(A=\dfrac{1}{2}\left(3^{101}-1\right)\)

a: Sửa đề: Trên BC lấy E sao cho BE=BA. Chứng minh ΔBAD=ΔBED

Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED

b: ta có: AK//BD

=>\(\widehat{DAK}=\widehat{ADB};\widehat{DKA}=\widehat{EDB}\)

mà \(\widehat{ADB}=\widehat{EDB}\)(ΔBAD=ΔBED)

nên \(\widehat{DAK}=\widehat{DKA}\)

=>DA=DK

=>DK=DE

=>D là trung điểm của KE

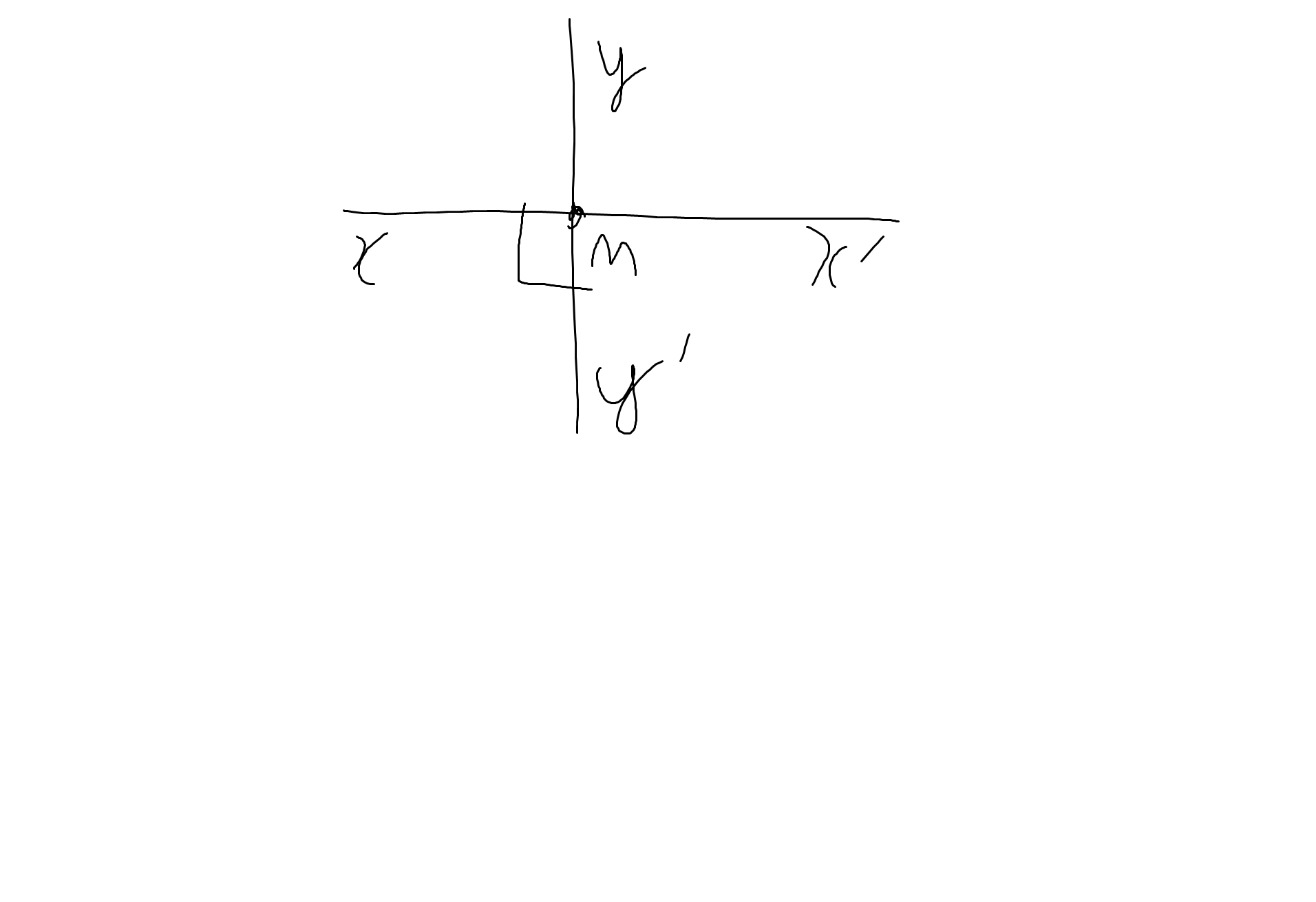
Ta có: \(\widehat{xMy'}=\widehat{x'My}\)(hai góc đối đỉnh)

mà \(\widehat{xMy'}=90^0\)

nên \(\widehat{x'My}=90^0\)

Ta có: \(\widehat{xMy'}+\widehat{x'My'}=180^0\)(hai góc kề bù)

=>\(\widehat{x'My'}=180^0-90^0=90^0\)

Ta có: \(\widehat{xMy}=\widehat{x'My'}\)(hai góc đối đỉnh)

mà \(\widehat{x'My'}=90^0\)

nên \(\widehat{xMy}=90^0\)

\(\sqrt{0,01}+\sqrt{0,04}+\sqrt{0,09}+...+\sqrt{0,81}\)

=0,1+0,2+0,3+...+0,9

=4,5

Bạn kiểm tra lại đề nhé.

Điều kiện; n nguyên
Ta có: \(\left(5\text{​​}n-9\right)⋮n\)
Vì \(5n⋮n\) nên \(-9⋮n\)
\(\Rightarrow n\inƯ\left(-9\right)=\left\{\pm1,\pm3,\pm9\right\}\) 9thỏa mãn)
Vậy...

Bổ sung: `n` thuộc `Z`

Ta có: `5n-9` và `n` thuộc `Z; n ≠ 0`

`5n - 9 ⋮ n`

Do `n ⋮ n => 5n ⋮ n`

`=> 9 ⋮ n`

`=> n` thuộc `Ư(9) =` {`-9;-3;-1;1;3;9`} (Thỏa mãn)

Vậy ...

Đặt \(A=-2^{49}-2^{48}-...-2^1-1\)
\(\Rightarrow-A=2^{49}+2^{48}+...+2^1+1\\ \Rightarrow-2A=2^{50}+2^{49}+...+2^2+2^1\\ \Rightarrow-A-\left(-2A\right)=\left(2^{49}+2^{48}+...+2^1+1\right)-\left(2^{50}+2^{49}+...+2^2+2^1\right)\\ A=1-2^{50}\)
Thay vào \(2^{50}-2^{49}-2^{48}-...-2^1-1\) được:
\(2^{50}-2^{49}-2^{48}-...-2^1-1\\ =2^{50}+1-2^{50}\\ =1\)

`S = 2^50 -2^49 -2^48 -...-2^1 -1`

`2S = 2^51 - 2^50 - 2^49 - ... - 2^2 - 2`

`2S - S = (2^51 - 2^50 - 2^49 - ... - 2^2 - 2) - (2^50 -2^49 -2^48 -...-2^1 -1)`

`S =  2^51 - 2^50 - 2^49 - ... - 2^2 - 2 - 2^50 +2^49 +2^48 +...+2^1 +1`

`S = 2^51 - 2^50 - 2^50  + 1`

`S = 2^51 - (2^50 + 2^50)  + 1`

`S = 2^51 - 2.2^50   + 1`

`S = 2^51 - 2^51   + 1`

`S = 1`