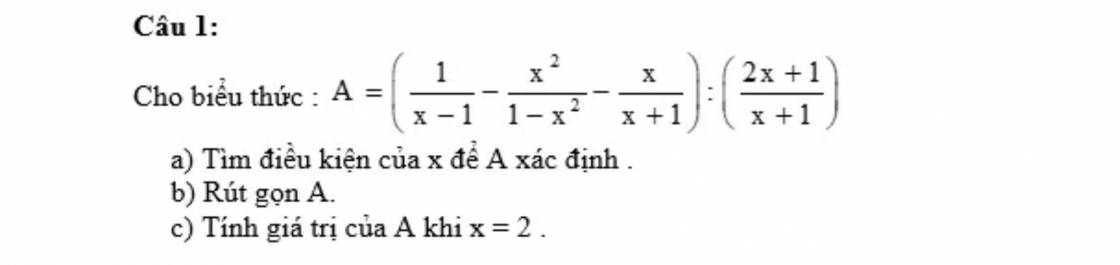

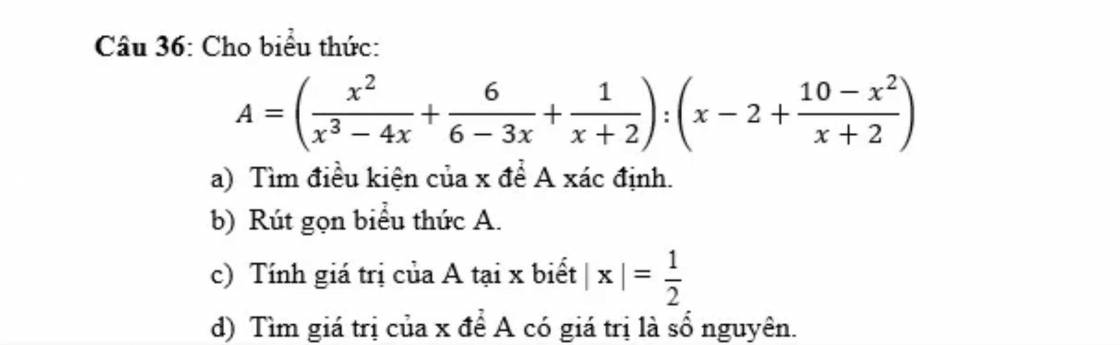
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$A=(2+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)$
$A=(2-1)(2+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)$
$=(2^2-1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)=(2^4-1)(2^4+1)(2^8+1)(2^{16}+1)$
$=(2^8-1)(2^8+1)(2^{16}+1)=(2^{16}-1)(2^{16}+1)=2^{32}-1$
P/s: Lần sau bạn lưu ý ghi đầy đủ yêu cầu đề bài.

Lời giải:
a. ĐKXĐ: $x\neq \pm 1$
b.
\(A=\left[\frac{x+1}{(x-1)(x+1)}+\frac{x^2}{(x-1)(x+1)}-\frac{x(x-1)}{(x+1)(x-1)}\right].\frac{x+1}{2x+1}\)
\(=\frac{x+1+x^2-(x^2-x)}{(x-1)(x+1)}.\frac{x+1}{2x+1}=\frac{2x+1}{(x-1)(x+1)}.\frac{x+1}{2x+1}=\frac{1}{x-1}\)
c.
Khi $x=2$ thì $A=\frac{1}{2-1}=1$

x2 + 3x + 3y + xy
= ( x2 + xy) + ( 3x + 3y)
= x( x + y) + 3 ( x + y)
= ( x + y) ( x + 3)

Theo Bezout đa thức F(n) = 2n2 + n - 18 chia hết cho đa thức n - 3
⇔ F(3) ⋮ n- 3 ⇔ 2.32 + 3 - 18 ⋮ n - 3 ⇔ 3 ⋮ n - 3
n - 3 ⋮ Ư(3) = { -3; -1; 1; 3} ⇔ n ϵ { 0; 2; 4; 6}

\(\dfrac{x^3\left(x-1\right)^3}{\left(x-1\right)^3}+\dfrac{x^3}{\left(x-1\right)^3}+\dfrac{3x^2\left(x-1\right)^2}{\left(x-1\right)^3}=28\)
ĐK: \(x\ne1\)
\(x^3+\dfrac{x^3}{\left(x-1\right)^3}+\dfrac{3x^2}{x-1}-28=0\)
\(x^3\left(x-1\right)^3+x^3+3x^2\left(x-1\right)^2-28\left(x-1\right)^3=0\)
\(\left(x^2-x\right)^3+3\left(x^2-x\right)^2+x^3-28\left(x^3-3x^2+3x-1\right)=0\)
\(\left(x^2-x\right)^3+3\left(x^2-x\right)^2+3\left(x^2-x\right)+1-\left(27x^3-81x^2+81x-27\right)=0\)
\(\left(x^2-x+1\right)^3-\left(3x-3\right)^3=0\)
\(\left(x^2-x+1-3x+3\right)\left[\left(x^2-x+1\right)^2+\left(x^2-x+1\right)\left(3x-3\right)+\left(3x-3\right)^2\right]=0\)
\(x^2-4x+4=0\)
\(x=2\) (TMĐK)


`-x^2+6x-11`
`=-x^2+6x-9-2`
`=-(x-3)^{2}-2`
Vì \(-(x-3)^{2} \le 0\)
\(<=>-(x-3)^{2}-2 \le -2\)
Hay \(-x^2+6x-11 \le -2\)
Dấu "`=`" xảy ra `<=>x-3=0<=>x=3`
-x2+6x-11
=>-(x2-6x+11)
=>-(x-3)2-2
vì-(x-3)2\(\le0\)
=>-(x-3)2-2\(\le\)-2
dấu bằng xảy ra khi x-3=0=>x=3
vậy gtln của -x2+6x-11 là -2 khi x=3
đúng cho like
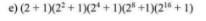
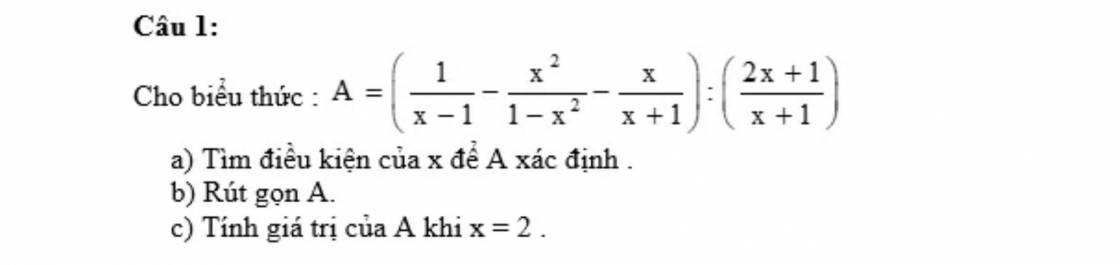
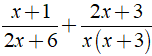
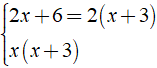 ⇒ MTC = 2x( x + 3 )
⇒ MTC = 2x( x + 3 )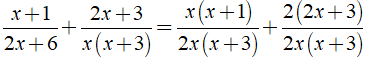
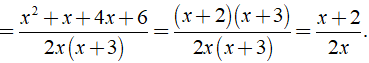
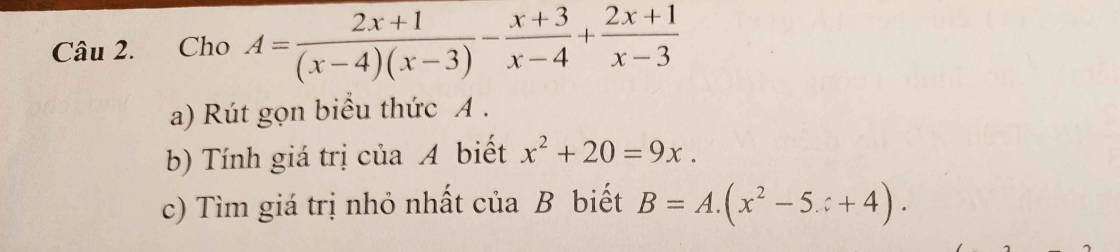
Em muốn hỏi bài nào vậy?
dạ bài 3 ạ